Although this expanded version of Quadibloc is a cipher with a 128 bit block size, I am not trying to detract from the importance of the candidate ciphers for the AES process. Prior to the deadline for a submission, I had considered a few designs, but I had nothing that I was quite satisfied with. Precisely because the other designs were now available to examine, I was able to find the "missing pieces" needed to complete a design.
This design allows key lengths of 128, 192, or 256 bytes, and in fact also allows keys of any length in the sequence starting 128, 144, 160, 176... provided that the key is not longer than 36 bytes times the number of rounds. The number of rounds can be 8, 12, 16, 20, 24, 28, 32, 36..., any multiple of 4 greater than or equal to 8.
One round of Quadibloc II takes perhaps 7 1/2 times as long as a round of DES, although a more optimistic estimate might be 3 3/4 times as long. Thus, 8-round Quadibloc II might manage to take less than 6 times as long as DES even with the initial estimate, and that would make Quadibloc II more efficient than Triple-DES. (The estimate is based on the fact that a round of DES requires eight fetches of a 32-bit quantity from a table; a round of Quadibloc II requires 24 fetches of a 32-bit quantity, and 24 fetches of an 8-bit quantity.)
This design also begins life with an unfair advantage: it partly results from the inspiration provided by the various AES candidates, and has, in fact, swiped good ideas from two or three of them at least. In any case, this design is proposed not as something that would have been a potential candidate were it not too late, but instead, particularly in its 32-round form, as something for those people who want a very secure block cipher without concern for efficiency.
Instead of two S-boxes, this design uses ten S-boxes generated from Euler's constant, by repeating the following process, the same one as used in the original QUADIBLOC:
As previously noted, I chose Euler's constant instead of, say, pi, because the mathematical theory behind Euler's constant is more complicated than that behind pi, which in turn is somewhat more complicated than e, the base of the natural logarithms.
The first four of these S-boxes are likely to be stored as arrays of 256 32-bit words, with the bits spread out reflecting the P permutation, which is again the same one as used in QUADIBLOC, and is as follows:
The bits 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 become 1 2 27 28 21 22 15 16 9 10 3 4 29 30 23 24 17 18 11 12 5 6 31 32 25 26 21 22 13 14 7 8
and this permutation is to be interpreted according to the following convention: the numbers in the bottom sequence identify the source of each bit in the permuted result in order.
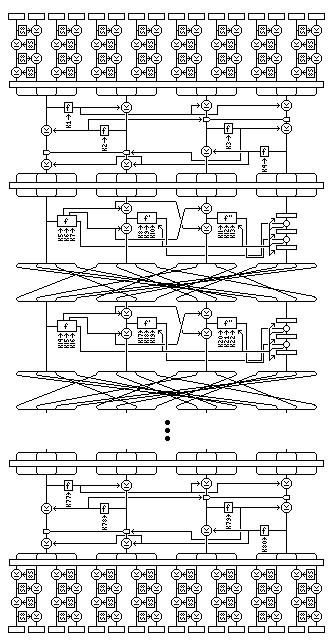
The round structure of Quadibloc II uses essentially the same f-function as was used in QUADIBLOC, with one addition: after the second substitution/permutation layer, and the third XOR of subkey material, the 32-bit subblock then goes through a key-dependent S-box. No permutation follows this S-box.
Three out of four 32-bit subblocks are used as input to f-functions. The f-function of the first subblock is used to supply additional inputs both to the other two f-functions and to the application of their outputs to the fourth subblock, which they modify.
There are other things going on in the round, and there are some minor changes to the f-function as well. The following diagram shows how the main part of a round proceeds:

The dotted lines show a part of the round which is required if less than 32 rounds are used, but which, involving as it does use of intermediate results from the f-function might produce some theoretical advantages if omitted.
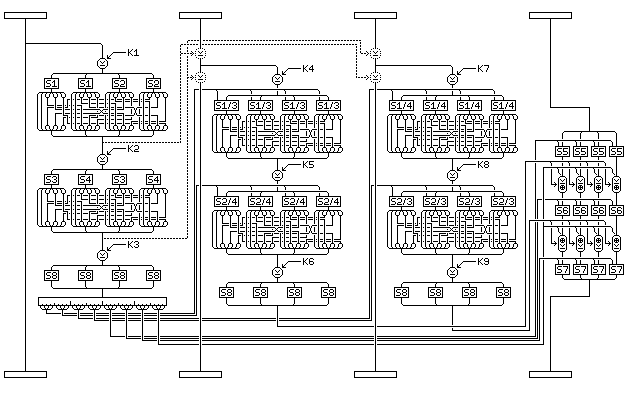
Before the regular rounds of Quadibloc II begin, and after they end, there is an additional phase of extra manipulations the purpose of which is to make life more difficult for the cryptanalyst. This phase is shown in the following diagram which gives an overview of Quadibloc II:
The wide boxes are the key-dependent byte permutations; the fixed permutations that take place between regular rounds are shown as wire crossings.
Initially, the block is divided into 16-bit units, which undergo substitution by means of a miniature block cipher of four Feistel rounds with the key-dependent S-box S8 as the f-function. First the leftmost byte in each pair of bytes is used to index into S8, finding the byte to XOR with the rightmost byte, and then it is done in the reverse direction, and so on, alternating for four rounds.
The 16 bytes of the block are rearranged according to a key-dependent permutation.
Then, each half of the block undergoes two rounds of Feistel encryption with a simplified f-function having only one S/P (substitution/permutation) layer. For faster diffusion, each f-function output is, in two of the rounds, XORed with the two subblocks in the other half of the block, and in the other two used to control swapping bits bitween those two subblocks, in the fashion pioneered by ICE. This operation is illustrated below:
The f-function consists of:
Four rounds are performed. In each round, the f-function of one subblock is XORed to the other subblock in the same half of the block. In the outer two rounds, that output is also XORed to the two subblocks in the other half; in the inner two rounds, it is used to control the swapping of bits between those two subblocks, a 1 bit corresponding to a bit position where swapping occurs, as was done in the block cipher ICE. The four subblocks are chosen in order, from left to right, as the input to the f-function.
Then, the bytes of the block are again rearranged according to a key-dependent permutation. A similar transformation takes place at the end. (MARS, of course, uses a different round structure before and after the main part of the cipher, but here the main idea swiped, but placed in a new form, is the idea of FROG. Instead of making the targets of XORs key-dependent, a key-dependent rearrangement of the bytes before a series of XORs achieves the same thing with a simpler key setup.)
The changes required to decipher in Quadibloc II are hinted at by the following diagram:
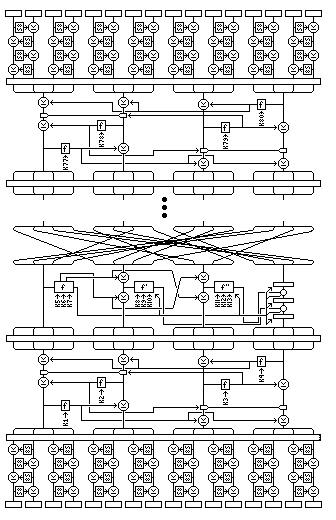
The initial and final miniature Feistel rounds need not be changed. The degenerate rounds with a short f-function have to operate on the four subblocks in reverse order, as well as using the subkeys in reverse order. The regular round experiences these changes: the steps changing the fourth subblock need to be reversed as well as being done in reverse order: thus, the substitution layers use the inverses of S7, S6, and S5; and the XOR/plus stages take the f-function of the third subblock first, then that of the second; also, more subtly, the order in which the two intermediate results of the f-function of the first subblock are XORed to the second and third subblocks are reversed.
The first four S-boxes generated above are called S1 through S4, and function as S-boxes with 8 inputs and 8 outputs in the first f-function. But in the next two f-functions, they are combined in pairs to form S-boxes with 9 inputs and 8 outputs. This is shown on the diagram: S1/S3 is an S-box that acts like S1 when the extra input is zero, and like S3 when the extra, most significant or leftmost, input is one.
S-boxes S1, S2, S3, and S4 are as given in the page on Euler's Constant and the Quadibloc S-boxes.
S5, S6, and S7 are also S-boxes with 9 inputs and 8 outputs, built up from the next six S-boxes generated from Euler's constant. Thus, when the MSB of input into S5 is zero, it produces as output the fifth generated S-box from the other 8 inputs, and when it is one, the sixth generated S-box is produced as output, and so on.
Thus, in this cipher, S-box S5 consists of S5 followed by S6; S-box S6 consists of S7 followed by S8; and S-box S7 consists of S9 followed by S10 where S5 through S10 are as given in the page entitled Euler's Constant and the Quadibloc S-boxes.
In detail, the round proceeds in this manner; and hopefully the diagram above will enable you to follow the lengthy description below:
This involved procedure constitutes the round. After each round except the last, a step corresponding to the swap of left and right halves of the block in DES is performed. Here, however, the movement of individual bytes is involved.
Bytes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
become
15 16 8 11 13 1 9 10 2 14 5 6 7 4 3 12
if the number of rounds is a multiple of 16, and
5 10 15 16 9 14 3 12 13 6 7 4 1 2 11 8
if that is not the case (but the number of rounds must still be a multiple of 4, and must be at least 8). Both byte permutations are presented as a series of 16 numbers giving the number of the source byte for each byte in the result in order.
Each round of Quadibloc II requires nine 32-bit subkeys. In addition, the extra scrambling phases at the beginning and end of the cipher require four subkeys each. Thus, 8-round Quadibloc II uses 80 subkeys, from K1 to K80, requiring 320 bytes of RAM.
The key for Quadibloc II must be at least eight bytes, or 64 bits, long, and may be any whole number of bytes up to twice the length of the total size of the subkeys plus sixteen bytes, or 128 bits. Many maximum-length keys will lead to duplicate internal key states of the cipher, of course; this maximum is an absolute maximum, beyond which some bits of the key will simply be ignored in the keying process.
As well, S8, the key-dependent S-box, is subkey material, and requires an additional 256 bytes of RAM. This total requirement of 576 bytes of RAM is the amount of storage needed for a key after key generation, which may have to be non-volatile in some applications; additional RAM is of course also needed for scratchpad storage in calculations, particularly during key generation.
Note: the bytes of S8 are stored as single bytes; they do not need to be expanded to four-byte entries to speed up a permutation, as is true of the fixed S-boxes S1 through S4, and the inverse of S8 is not required for deciphering, unlike S-boxes S5 through S7; the S-box requiring the least storage was chosen as the key-dependent one. (Having a key-dependent S-box, of course, is a way to achieve a high degree of resistance to differential and linear cryptanalysis.)
Initially, the subkeys are filled in the following order:
K1 K2 K3 K4 K5 K8 K11 K6 K9 K12 K7 K10 K13 K14 K17 K20 K15 K18 K21 K16 K19 K22 K23 K26 K29 K24 K27 K30 K25 K28 K31 ... K68 K71 K74 K69 K72 K75 K70 K73 K76 K77 K78 K79 K80
and so on; thus the subkeys are filled for one round before going on to the next, but the first subkey for each f-function is filled before the second subkey for each f-function, and so on.
The subkeys for the degenerate rounds are just filled in numerical order, the first four at the start, and the last four at the end.
They are filled from the following sources, in turn:
First, the actual key is placed directly into the subkeys. It must consist of a whole number of bytes, and be at least eight bytes long, for the rest of the procedure to work.
Next, generate additional bytes of initial subkey material as follows:
Fill A1, A2, A3, and B1, B2, B3, B4, and B5 with the first eight bytes of the key in order. Initialize the variable Q to be zero.
Split the key into two pieces as follows, where L is the number of bytes in the key:
In the first case, the lengths of the two pieces of the key are two consecutive numbers, one even, and one odd. In the second case, the lengths of the two pieces of the key are two odd numbers, differing by two. In the third case, the lengths of the two pieces of the key are two odd numbers, differing by four. In all three cases, the lengths of the two pieces of the key are relatively prime, and uniquely identify the length of the original key.
Each group of bytes is then used as the initial contents of a shift register, which operates as follows:
The sum of the first and third bytes in the shift register is XORed with the second-last byte in the shift register. The result is used as the output of the shift register, and is also used as the new last byte in the shift register, all other bytes being moved to the next earlier place, the first byte being discarded.
For each byte generated by XORing the outputs from the two shift registers, that byte is then transformed by carrying out the following instructions:
For each of the numbers 0 to 4, do the following:
Modify the variables B1 through B5 by adding the results of this process for the numbers 0 to 4, respectively, to them. (This is a permanent change; for each byte generated, new values are added to them, and the totals are cumulative.)
Now, generate a byte from the two shift registers containing the two unequal pieces of the key as outlined above. Add Q to that byte. Put that byte through the following process:
The result of this process is the output byte, to be placed in the subkeys. The output byte is also stored in the variable Q.
One more step, however, remains in the process; the variables A1, A2, and A3 are changed (just as B1 through B5 have already been changed) as follows: increment A2. If A2 wraps around, being incremented from 255 to zero, increment A1. If A1 wraps around, increment A3.
An initial value for S8, the key-dependent S-box is generated as follows:
The key-dependent byte transpositions used at the beginning and end of the cipher are derived from the key-dependent S-box S8 as follows: the first permutation consists in taking bytes 0, 1, ... 16 to the bytes indicated by the least significant nibbles of the S-box entries in S8 of the form 0x in hexadecimal, taken in the order they are found. Note that this builds up the permutation in "dispatch" form, while all the fixed permutations in this description of Quadibloc II are given in "fetch" form. The second permutation is built up from the bytes of the form 1x in hexadecimal. The third one, which takes place after the rounds are completed, is the inverse of the one built up from the bytes of the form 9x in hexadecimal, and the fourth one is the inverse of the one built up from the bytes of the form 8x in hexadecimal.
Then, the actual key sequence used for encipherment is generated by the following procedure:
Using the last 128-bits of the key, if the key is 128 bits long or more, or the key repeated as many times as required to fill a 128-bit block otherwise (starting from the beginning, not the end and working backwards) as the plaintext block, encipher it using the initial key schedule generated above, but with the following modifications.
The intermediate results of all three f-functions are saved. The following nine 32-bit words are produced from each round of the encipherment process:
Also, the degenerate rounds produce their f-function outputs as well, so exactly one 32-bit output is produced for every subkey.
After each round of the encipherment process which is used to generate the final subkeys, the nine words above are XORed to nine subkeys. The four f-function outputs of the degenerate rounds are also used, so the number of words used equals the number of subkeys; each set of four degenerate rounds is treated as a single round in that the four results are not applied to the subkeys until the set of four rounds has been performed completely. The sequence of subkeys to which they are applied is as follows (reading across):
K80 K76 K67 ... K49 K40 K31 K22 K13
K79 K75 K66 ... K48 K39 K30 K21 K12
K78 K74 K65 ... K47 K38 K29 K20 K11
K77 K73 K64 ... K46 K37 K28 K19 K10
K72 K63 ... K45 K36 K27 K18 K9
K71 K62 ... K44 K35 K26 K17 K8 K4
K70 K61 ... K43 K34 K25 K16 K7 K3
K69 K60 ... K42 K33 K24 K15 K6 K2
K68 K59 ... K41 K32 K23 K14 K5 K1
thus, first the last subkey of each round is modified, then the second-last subkey of each round, and so on. The subkeys are modified before the encipherment is completed, but only after each round is completed. The subkeys used in the degenerate rounds are placed in the sequence as well as possible. The intermediate values applied are taken from those generated by the subkeys in their numerical order.
Once the subkeys have been modified in this manner, if the size of the key was greater than the total size of the subkeys, any remaining bytes in the key are to be XORed with the subkeys that are now present, using the same order as was used for initially filling the subkey space,
K1 K2 K3 K4 K5 K8 K11 K6 K9 K12 K7 K10 K13 ...
et cetera.
Allowing the key to be larger than the total size of the subkeys, of course, doesn't make sense after a point; but if the excess is small, the main result is to make it possible for the same set of subkeys to be accompanied by different values of the key-dependent S-box S8.
Then, the same procedure used to generate the initial value of S8 from the initial subkeys is applied to the final subkeys. Since the subkeys may not have enough bytes in them to supply the permutation-generating process, the SIGABA-like procedure of generating additional bytes is used again, as done previously for generating the initial value of S8. Once again, A1 through B5 are filled from the last eight subkey bytes, and the earlier subkey bytes are divided into two almost equal parts as was done with the key previously.
The generated result, however, is not used as the final value of S8. Instead, each element of S8 is replaced by the value it points to in this result; that is, for N from 0 to 255, S8(N) becomes R(S8(N)). (Thus, S8 depends on both the old and new subkeys, and doesn't relate to the current subkeys in a simple way.)
The new value of S8 is also used as the old value was above to provide the four key-dependent byte transpositions which begin and end the cipher.
One may, if one wishes, see the view of the subkeys (other than those of the degenerate rounds) as belonging to a rectangular prism of 32-bit words, accessed in three different directions, as evocative of Rijndael.
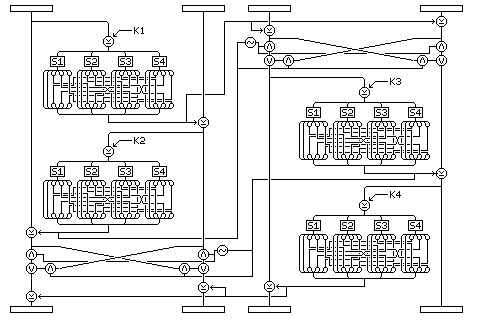
If you have time to encipher your data with 40 rounds of Quadibloc II, I have a variation for you. A diagram giving an overview of this variation is provided.
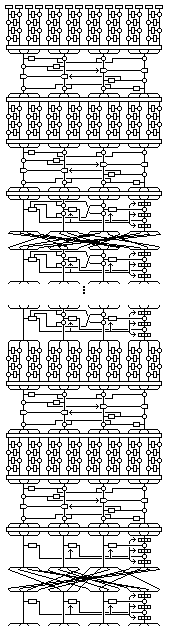
First, the tiny Feistel rounds, the key-dependent byte permutation (derived from the 0x bytes), the initial degenerate four-subkey series of rounds, and another key-dependent byte permutation (derived from the 1x bytes), then a second layer of tiny Feistel rounds, another key-dependent byte permutation (derived from the 4x bytes), another series of four degenerate rounds, and another key-dependent byte permutation (derived from the 5x bytes).
Then, four rounds of Quadibloc II, with the byte interchange after the first three rounds following the pattern for a multiple of four rounds that is not a multiple of 16 rounds.
Now, the whitening sequence is repeated, again first with a series of miniature Feistel rounds.
Then, another key dependent byte permutation, derived from the elements of S8 in the form 2x.
Another degenerate four rounds.
Key-dependent byte permutation, derived from the 3x elements in S8.
Miniature Feistel rounds, permutation (6x), degenerate four rounds, permutation (7x).
Thirty-two rounds of Quadibloc II, but with the additional XORs of the second and third subblocks with the two intermediate values from the f-function of the first subblock omitted. Byte interchange after the first 31 of these rounds is as for a multiple of 16 rounds.
Key-dependent byte permutation, the inverse of the one derived from the elements of S8 of the form Fx.
Another degenerate four rounds.
Inverse Ex from S8 byte transposition.
Miniature Feistel rounds in inverse form.
Key-dependent byte permutation, the inverse of the one derived from the elements of S8 of the form Bx.
Another degenerate four rounds.
Inverse Ax from S8 byte transposition.
Miniature Feistel rounds in inverse form.
Four rounds of Quadibloc II.
The final three-step whitening sequence, plus the tiny Feistel rounds, and byte transpositions, all repeated twice. Byte transpositions are the inverses of those derived from the elements of S8 in the forms Dx, Cx, 9x, and 8x.
By restricting the perhaps dangerous - but diffusion-enhancing - XOR of intermediate results to the outer eight Quadibloc rounds, one has a diffusing outer part and a secure core. This, of course, comes even closer to the design of MARS.
Note that for this variation, when the keys are initially filled, the thirty-two subkeys for the four sets of degenerate rounds stand outside the sequence; sixteen at the start, and sixteen at the end, and when the keys are modified, the subkeys for the first four degenerate rounds are at the left of the top four rows, those for the last four at the right of the bottom two rows.
Thus, the order for initially filling the keys is as follows:
K1 K2 K3 K4 K5 K6 K7 K8 K9 K12 K15 K10 K13 K16 K11 K14 K17 K18 K21 K24 K19 K22 K25 K20 K23 K26 K27 K30 K33 K28 K31 K34 K29 K32 K35 K28 K39 K42 K37 K40 K43 K38 K41 K44 K45 K46 K47 K48 K49 K50 K51 K52 K53 K56 K59 K54 K57 K60 K55 K58 K61 ... K332 K335 K338 K333 K336 K339 K334 K337 K340 K341 K342 K343 K344 K345 K346 K347 K348 K349 K352 K355 K350 K353 K356 K351 K354 K357 ... K376 K379 K382 K377 K380 K383 K378 K381 K384 K385 K386 K387 K388 K389 K390 K391 K392
and the order for adjusting the keys from f-function outputs and intermediate results is:
K392 K388 K348 K344 K384 K375 K366 K357 K340 ... K26 K17
K391 K387 K347 K343 K383 K374 K365 K356 K339 ... K25 K16
K390 K386 K346 K342 K382 K373 K364 K355 K338 ... K24 K15
K389 K385 K345 K341 K381 K372 K363 K354 K337 ... K23 K14
K380 K371 K362 K353 K336 ... K22 K13
K379 K370 K361 K352 K335 ... K21 K12 K52 K48 K8 K4
K378 K369 K360 K351 K334 ... K20 K11 K51 K47 K7 K3
K377 K368 K359 K350 K333 ... K19 K10 K50 K46 K6 K2
K376 K367 K358 K349 K332 ... K18 K9 K49 K45 K5 K1
Other modifications to Quadibloc II are possible. The following illustration:
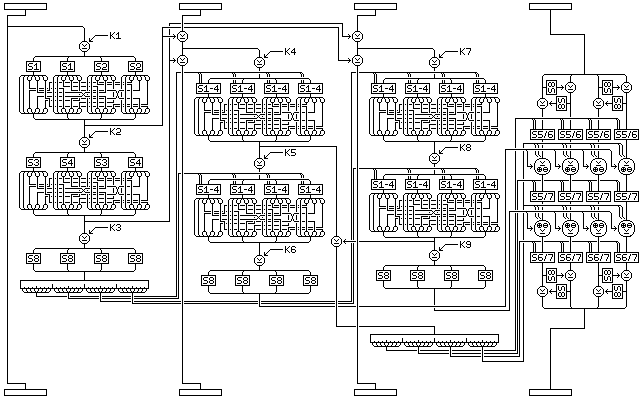
shows how the basic Quadibloc II round can be modified to double the size of the S-boxes in the f-functions for the second and third subblocks; one S-box, made from S-boxes 1 through 4 is used, so two extra nonlinearity bits are used as input. This function uses all 32 nonlinearity control bits produced as the output of the f-function of the first subblock.
Instead of using S-boxes S5 through S7 singly, they are used in pairs on the fourth subblock, and so the extra nonlinearity bits required here are doubled as well. An additional 32 nonlinearity control bits are created from the XOR of one intermediate result from the f-function of the second subblock and the other intermediate result from the f-function of the third subblock. As switching between addition and XOR for applying the f-function outputs directly to the fourth subblock requires only one bit per byte, the remaining four bits are used to switch the addition operation to a subtraction operation.
The other major modification in this extended variant of the basic round is to use S8 in the same method as used in the initial whitening phase to promote diffusion within the fourth subblock.
However, I find the following variation on the basic Quadibloc II round even more interesting:
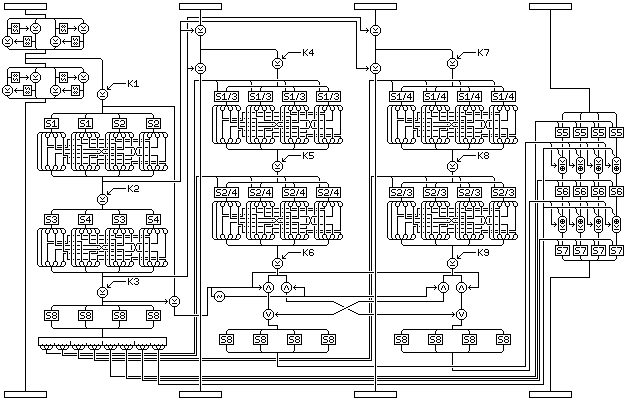
Here, two other intermediate values in the f-function of the first subblock are used to form a 32-bit value used for an ICE-style interchange between the f-functions of the second and third subblocks. The interchange takes place just before S8 is applied, thus ensuring it significantly alters the f-function outputs applied to the fourth subblock. As well, a micro-Feistel layer is used, as in the doubled nonlinearity variant, but this time to modify the first subblock, so that all four subblocks are changed, and changed in a key-dependent way by every round (the changes to the first three subblocks depend on the first subblock as well as the key, while those to the fourth subblock depend on all of the first three subblocks).
To proceed further, we can also have the following type A round:
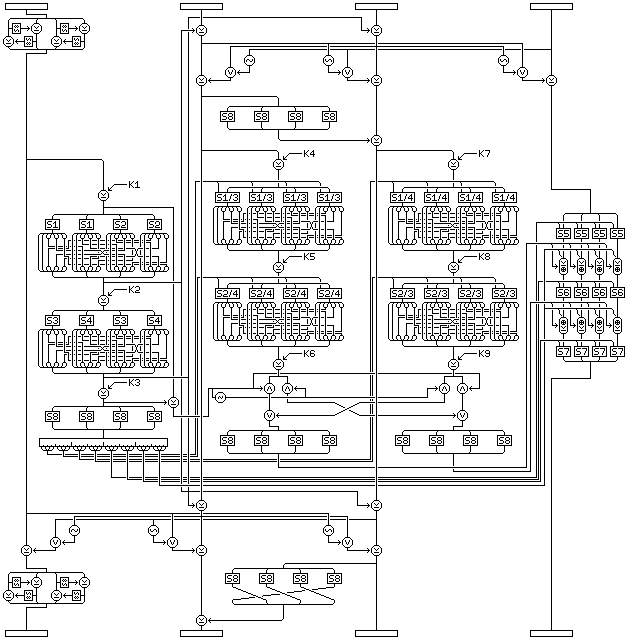
with its corresponding round of type B:
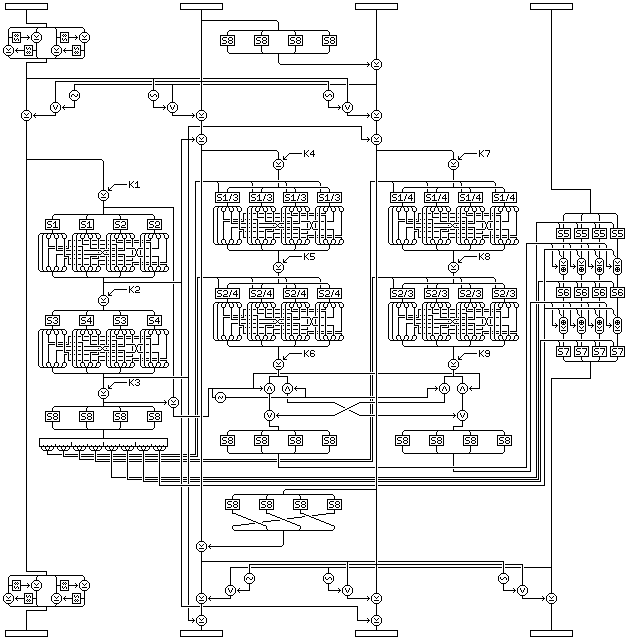
which adds some additional operations to the round structure. Not wishing to give up being endian-neutral, instead of throwing in a Pseudo-Hadamard Transform between the second and third subblocks, I used an XOR but used S8 to avoid it cancelling out. The intent is merely to have an alteration to those subblocks that is slightly more involved than a simple XOR of intermediate f-function results from the first subblock, but a little bit of propagation between bytes is achieved by displacing bytes before the second XOR.
Also added is an interaction, taken from the block cipher 3-Way, between three of the subblocks. This places a very small (3 bits input and output) nonlinear S-box in the cipher that operates on corresponding bits in the three subblocks. Since it either operates on all but the first subblock, or all but the fourth subblock, two round types were required to make the cipher equally secure against attacks from either direction. (The deciphering form of the round could also be used, but that of course creates the slim possibility of some rounds partly undoing the work of other rounds.)
Since each bit of the output is the bit of the input XOR a function of the other two bits that is 1 most of the time, the identities of the bits are in a sense preserved; thus, it does not appear that the apparent danger of information leaking past the involved transformation of the fourth subblock is a genuine concern. In addition, the type A rounds are used at the beginning, and the type B rounds at the end, so that any leakage is towards the inside of the block cipher rather than towards the outside.
Since the first subblock is aloof from the values and changes in the other three subblocks, the interaction between the last three subblocks does not prevent the round from being invertible, even though it happens after the XOR of intermediate results from the f-function of the first subblock. The interaction between the first three subblocks does not prevent the round from being invertible, because the operations taking place before it are all self-contained.
In analyzing Quadibloc II, it may be interesting to examine how it could be attacked if part of the internal key is known. If S8 is known, Quadibloc II becomes a more conventional block cipher. Is the conventional part of it still reasonably strong? If the conventional subkeys, but not S8, are known, but not the intermediate subkey values, can part of the generation of S8 still be retraced? With only a small part of the internal operations of the cipher controlled by the secret part of the key, can cryptanalysis trace enough to obtain information about S8?
The block cipher Quadibloc XI in this series has a secure key schedule which appears to me both efficient and secure. Quadibloc II RK (Revised Keys) may denote the variant which uses that key schedule as follows: generate the four bytes of each subkey in order, most significant (leftmost) first, generating the keys in simple numerical order from K1 to K392, and then use the method for generating a permutation to produce S8.
One modification is required, however; instead of using S3 as the S-box, one that is never used in the cipher itself is to be used; and the first one satisfying that criterion is the constant S-box produced from Euler's Constant listed on the page Euler's Constant and the Quadibloc S-boxes as S11, since the S5, S6, and S7 referred to on this page are (S5, S6), (S7, S8), and (S9, S10) as noted on that page.
For this method of subkey generation, the key must be a multiple of four bytes in length.
This revised form of subkey generation proceeds as follows:
Three strings of bytes of different length are produced from the key.
The first string consists of the key, followed by one byte containing the one's complement of the XOR of all the bytes of the key.
The second string consists of the one's complements of the bytes of the key in reverse order, with three bytes appended containing the following three quantities:
The third string consists of alternating bytes, taken from the bytes of the key in reverse order, and then from the bytes of the one's complement of the key, and then that string is followed by the one's complements of the first four bytes of the key.
Thus, if the key is:
128 64 32 16 8 4 2 1 1 2 3 4 5 6 7 8
then the strings generated from it are as follows:
First string: 128 64 32 16 8 4 2 1 1 2 3 4 5 6 7 8 8 Second string: 247 248 249 250 251 252 253 254 254 253 251 247 239 223 191 127 37 170 93 Third string: 8 127 7 191 6 223 5 239 4 247 3 251 2 253 1 254 1 254 2 253 4 252 8 251 16 250 32 249 64 248 128 247 127 191 223 239
Given that the length of the key is 4n, the lengths of the three strings are 4n+1, 4n+3, and 8n+4, and hence all three are relatively prime, since both 4n+1 and 4n+3 are odd, and 8n+4 is two times 4n+2.
Two buffers, each containing room for 256 bytes, are filled by generating bytes from the first and second strings by placing them in a nonlinear shift register.
The form of that shift register is shown in the following illustration, showing its precise form for the first string (but with S11 replaced by S3, as this is the diagram from the page on Quadibloc XI).
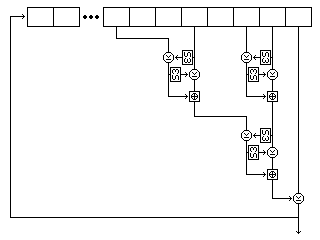
Five bytes are read from the string at each step. For the first string, they are, as shown in the diagram, the eighth-last, fifth-last, third-last, and second-last bytes and the last byte. For the second string, they are the eighth-last, seventh-last, fourth-last, and second-last bytes, and the last byte. For the third string, they are the twelfth-last, tenth-last, seventh-last, and fourth-last bytes, and the last byte.
Each time the shift register produces a byte, it does so as follows:
Both buffers contain 256 bytes. The first buffer, called buffer A, is filled with 256 successive bytes generated from the second string by means of the nonlinear shift register filled with the second string. The second buffer, called buffer B, is filled with 256 successive bytes generated from the first string by means of the nonlinear shift register filled with the first string.
Once the setup is complete, subkey material is generated one byte at a time, the first byte generated being the leftmost byte of subkey K1, and so on.
A subkey byte is generated as follows:
The following diagram attempts to illustrate the complete process of subkey byte generation (but with S-box S11 replaced by S-box S3, because it is the diagram from the page on Quadibloc XI):
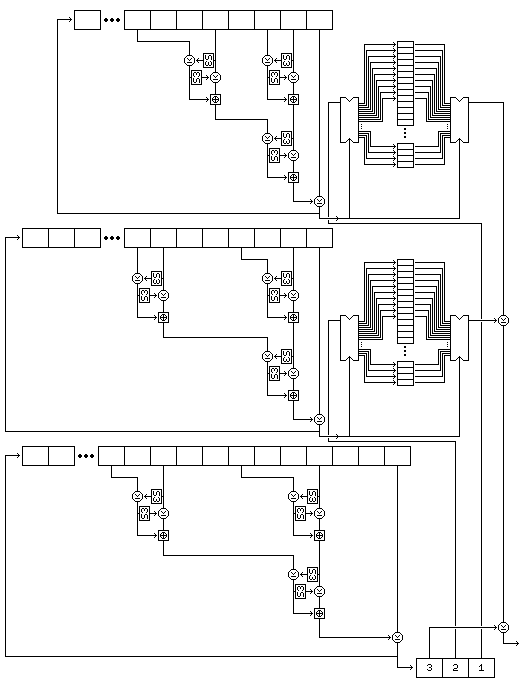
Note that this procedure, since it exercises the two strings used to select bytes, rather than the string used to generate values, results in a small change in the key resulting in large changes in the subkeys from the very beginning.
Once all the required 32-bit subkey words are generated, the key-dependent S-box S8 must be generated. To generate this bijective S-box, the following procedure is used:
The resulting contents of buffer D are used as the key-dependent bijective S-box intended to be produced.
This procedure, although it uses buffers A and B, leaves them undisturbed; thus, byte generation may continue after one S-box is produced.
Next
Start of Section
Skip to Next Chapter
Skip to Next Section
Table of Contents
Main Page
Home Page