Quadibloc III includes the round structure of SKIPJACK as a component. The cipher SKIPJACK may be protected by patents, preventing this cipher from being generally available for use in its present form. (Quadibloc III was designed some time after the SKIPJACK algorithm had been declassified, and it is of course from the publication of that algorithm following that event that I learned its inner workings.) |
Quadibloc III is an extension of Quadibloc II which uses a different type of block cipher as its inner core. It too uses a 128-bit block size. Unlike Quadibloc II, which, at least with only eight full rounds, is not too much slower than a typical AES candidate (although it isn't fully clear to me if eight rounds is enough for security), Quadibloc III, while secure, is clearly too slow and complicated to be useful for practical purposes. Its value is that it illustrates a number of concepts which may be useful in ciphers of a more practical size.
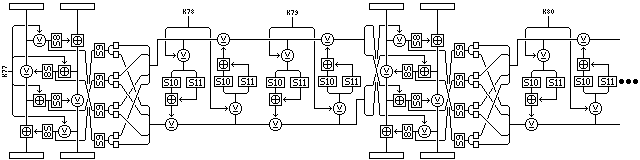
Here is a diagram giving an overview of the structure of Quadibloc III, to accompany a description of its rounds:
The steps in the cipher are symmetric, and they are as follows:
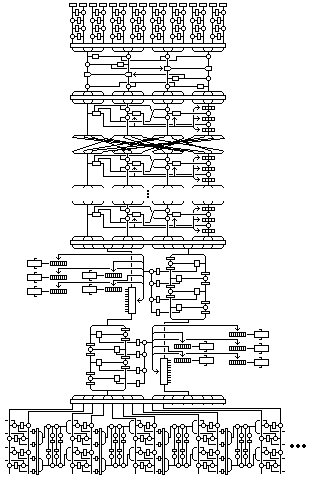
The following diagram illustrates the method used for the middle 16 rounds of Quadibloc III:

Using four eight-bit subkeys (derived from a single 32-bit subkey, to remain within the overall structure derived from Quadibloc II), four Feistel rounds are used to encipher a 16-bit subblock; in the first round, the right half is XORed with the first subkey, then replaced through S8, then added to the left half. The direction of the f-function alternates from right to left to left to right, and in the two outer rounds, the subkey is XORed and the f-function output added, and in the two inner rounds, the subkey is added and the f-function output XORed.
The four intermediate results of the f-functions, derived before S8 substitution, are used to index into the fixed S-box S9. The S-box outputs are used to form a 32-bit word consisting of the first nibbles of the four substituted results in order, then the second nibbles. (Since, looking sideways, the bottom, rather than the top, of the previous four rounds are to the left, the diagram shows that the order needs to be reversed when drawing a left-to-right round of this cipher, by means of a twist upon entry and exit from the horizontal Feistel rounds.)
The resulting 32-bit word is then itself enciphered by four Feistel rounds of a cipher which, like Blowfish, uses wide key-dependent S-boxes in the f-function. Here, four 16-bit subkeys are used, and so they are derived from two 32-bit regular subkeys.
The final interchange is not omitted, or the rounds can be thought of, as they are drawn, in in-place format, and the first round goes from right to left (or, in the diagram, top to bottom).
If the first set of four Feistel rounds operating on a 16-bit subblock is denoted by 1, the second by 2, and angle brackets are used to show how one round provides the subkey input for the next, the pattern of rounds used in this phase is as follows:
1 > 2 > 3 > 4 > 5 > 6 > 7 > 8 < 7 < 6 < 5 < 4 < 3 < 2 < 1 8 < > 8 1 > 2 > 3 > 4 > 5 > 6 > 7 > 8 < 7 < 6 < 5 < 4 < 3 < 2 < 1 > 7 > 8 1 > 2 > 3 > 4 > 5 > 6 > < 1 8 < 7 < 6 < 5 < 4 < 3 < 2 < > 6 > 7 > 8 1 > 2 > 3 > 4 > 5 > < 2 < 1 8 < 7 < 6 < 5 < 4 < 3 < > 5 > 6 > 7 > 8 1 > 2 > 3 > 4 > < 3 < 2 < 1 8 < 7 < 6 < 5 < 4 < > 4 > 5 > 6 > 7 > 8 1 > 2 > 3 > < 4 < 3 < 2 < 1 8 < 7 < 6 < 5 < > 3 > 4 > 5 > 6 > 7 > 8 1 > 2 > < 5 < 4 < 3 < 2 < 1 8 < 7 < 6 < > 2 > 3 > 4 > 5 > 6 > 7 > 8 1 > < 6 < 5 < 4 < 3 < 2 < 1 8 < 7 <
The S-box S9 is fixed, and is generated by continuing the process used for generating S-boxes 1 through 7 from Euler's constant to generate one more permutation of the numbers 0 through 255, therefore this S-box is the one designated S11 on the page entitled Euler's Constant and the Quadibloc S-Boxes.
The concept of a cipher called Mishmash is noted in the conclusions section of this chapter, to which reference may be required.
The left half of the block (in the second round, the right half) is enciphered using four rounds of Quadibloc. The intermediate results, after XORing in the second of the three subkeys, of each of the four f-function outputs are then subjected to the Quadibloc f-function again, with another twelve subkeys, and the four 32-bit outputs are XORed together.
The 32-bit result controls the encipherment of the right half of the block. The right half of the block is enciphered by cipher steps 1 through 5. The first 25 bits of the 32-bit result is divided into five 5-bit values, indicating for each of the five cipher steps, in order of their numeric labels, which of 32 sets of subkey material is used for them.
The last 7 bits of the 32-bit result indicates the order in which the five cipher steps take place. Values 0 through 119 of these seven bits give the 120 permutations of the numbers from 1 through 5 in numerical order, as shown in the following table:
0 12345 24 21345 48 31245 72 41235 96 51234 1 12354 25 21354 49 31254 73 41253 97 51243 2 12435 26 21435 50 31425 74 41325 98 51324 3 12453 27 21453 51 31452 75 41352 99 51342 4 12534 28 21534 52 31524 76 41523 100 51423 5 12543 29 21543 53 31542 77 41532 101 51432 6 13245 30 23145 54 32145 78 42135 102 52134 7 13254 31 23154 55 32154 79 42153 103 52143 8 13425 32 23415 56 32415 80 42315 104 52314 9 13452 33 23451 57 32451 81 42351 105 52341 10 13524 34 23514 58 32514 82 42513 106 52413 11 13542 35 23541 59 32541 83 42531 107 52431 12 14235 36 24135 60 34125 84 43125 108 53124 13 14253 37 24153 61 34152 85 43152 109 53142 14 14325 38 24315 62 34215 86 43215 110 53214 15 14352 39 24351 63 34251 87 43251 111 53241 16 14523 40 24513 64 34512 88 43512 112 53412 17 14532 41 24531 65 34521 89 43521 113 53421 18 15234 42 25134 66 35124 90 45123 114 54123 19 15243 43 25143 67 35142 91 45132 115 54132 20 15324 44 25314 68 35214 92 45213 116 54213 21 15342 45 25341 69 35241 93 45231 117 54231 22 15423 46 25413 70 35412 94 45312 118 54312 23 15432 47 25431 71 35421 95 45321 119 54321
and the remaining values give the following eight preferred orders once again:
120 31425 121 32415 122 51423 123 52413 124 31524 125 32514 126 41523 127 42513
Only one pool of 32 subkey values is used by all four Mishmash rounds in the cipher (which is different from the Mishmash concept described in the conclusions section), despite the danger that a subkey may be used more than once.
The five cipher steps are:
In the Mishmash rounds, the final interchange is not omitted after the DES and Quadibloc rounds, since they are part of an ongoing block cipher. This is true also of the Mishmash concept, as can be seen from the diagrams, which show the ciphers in in-place form.
The four Skipjack rounds are type A in the first two Mishmash rounds in the cipher, and type B in the last two. In addition, the SAFER rounds in the last two Mishmash rounds are rounds of SAFER decryption instead of SAFER encryption, for the same reason.
Subkey generation for Quadibloc III follows the same general scheme as for Quadibloc II; initial subkeys are generated using a method similar to the one used in Quadibloc II, but somewhat more elaborate.
Fill A1, A2, and A3; B1, B2, B3, B4, and B5; and C1, C2, C3, C4, and C5 with the first thirteen bytes of the key in order. Initialize the variable Q to be zero.
Split the key into two pieces as follows, where L is the number of bytes in the key:
In the first case, the lengths of the two pieces of the key are two consecutive numbers, one even, and one odd. In the second case, the lengths of the two pieces of the key are two odd numbers, differing by two. In the third case, the lengths of the two pieces of the key are two odd numbers, differing by four. In all three cases, the lengths of the two pieces of the key are relatively prime, and uniquely identify the length of the original key.
Each group of bytes is then used as the initial contents of a shift register, which operates as follows:
The sum of the first and third bytes in the shift register is XORed with the second-last byte in the shift register. The result is used as the output of the shift register, and is also used as the new last byte in the shift register, all other bytes being moved to the next earlier place, the first byte being discarded.
For each byte generated by XORing the outputs from the two shift registers, that byte is then transformed by carrying out the following instructions:
For each of the numbers 0 to 4, do the following:
Modify the variables B1 through B5 by adding the results of this process for the numbers 0 to 4, respectively, to them. (This is a permanent change; for each byte generated, new values are added to them, and the totals are cumulative.)
Once that has been done, using the modified values of B1 through B5, we once again use the numbers 0 to 4 in order as inputs as we do the following:
Modify the variables C1 through C5 by adding the results of this process for the numbers 0 to 4, respectively, to them. (This is a permanent change; for each byte generated, new values are added to them, and the totals are cumulative.)
Now, generate a byte from the two shift registers containing the two unequal pieces of the key as outlined above. Add Q to that byte. Put that byte through the following process:
The result of this process is the output byte, to be placed in the subkeys. The output byte is also stored in the variable Q.
One more step, however, remains in the process; the variables A1, A2, and A3 are changed (just as B1 through B5 have already been changed) as follows: replace A1 with the former contents of A2; replace A2 with the former contents of A3; and replace A3 with the former contents of A3 XOR the current output byte (also stored in Q).
After generating the first 440 regular 32-bit subkeys, initial values of the remaining subkey material is generated in the following order:
All the subkey material thus generated, except the material used to produce S-box S8, is retained in order in an array for later modification.
An initial value for S8, the key-dependent S-box is generated as follows:
Only the first 440 subkeys, each 32-bits long, which are the first subkey material generated by this method, are modified by the key augmentation technique of performing an initial encipherment, and XORing subkeys with intermediate results. Because some of the rounds do not produce intermediate results suitable for this use, the key augmentation step undergoes an important change. Instead of modifying the 440 subkeys by performing a normal Quadibloc III encipherment, and using its intermediate results, a modified encipherment, using only normal rounds found in Quadibloc II is used.
The modified encipherment consists of one group of four degenerate rounds, forty-eight normal Quadibloc II rounds, and one more group of four degenerate rounds. This arrangement uses exactly 440 subkeys. Four key-dependent byte permutations are used, from 0x, 1x, and inverse 9x and 8x; only one unkeyed whitening step, followed by the 0x permutation, begins the cipher; the 1x permutation follows the first group of four degenerate rounds, preceding the first conventional Quadibloc II round.
The subkeys are initially filled in the following order, consistent with Quadibloc II practice:
K1 K2 K3 K4 K5 K8 K11 K6 K9 K12 K7 K10 K13 K14 K17 K20 K15 K18 K21 K16 K19 K22 ... K428 K431 K434 K429 K432 K435 K430 K433 K436 K437 K438 K439 K440
and are modified during key enrichment in the following order (although the subkeys are aligned in columns to illustrate their pattern, the order used is that found by reading across):
K440 K436 ... K22 K13
K439 K435 ... K21 K12
K438 K434 ... K20 K11
K437 K433 ... K19 K10
K432 ... K18 K9
K431 ... K17 K8 K4
K430 ... K16 K7 K3
K429 ... K15 K6 K2
K428 ... K14 K5 K1
Bytes for use in the 48 additional subkeys, S10 and S11, and in Mishmash, are generated during the initial part of subkey generation, even though these parts of the cipher aren't used in key-enrichment; then, during the key-enrichment phase, nine bytes of output from the same shift register process as was used to fill all the subkey material with its initial values, but modified in an analogous fashion to that used for Quadibloc II (the last 13 bytes of the 440 regular subkeys are used to fill A1 through C5, and one shift register, rather than two, is used, consisting of the rest of the subkey material), are used to modify eight bytes in this additional subkey material.
This is done as follows: the first byte determines the use of the next eight bytes; if its most significant bit is a 1, the next byte is XORed to the previously generated byte, if its most significant bit is a 0, the next byte replaces the corresponding previously generated byte, and so on through the bits of the first byte and the bytes following.
The additional subkey material being modified in this step consists of 7488 bytes. For the purpose of an additional operation to be performed concurrently with the XOR or replacement of these bytes in groups of eight using generated bytes in groups of nine, these bytes are to be considered as 20 blocks of 256 bytes each, plus 64 extra bytes.
The additional manipulation to be performed consists of two steps. Only during the processing of the second through the 19th of the 20 complete blocks are both steps done; one is done during the processing of the first block.
For each of the first 256 generated bytes of the 288 generated bytes required to modify the 256 bytes of the current block, the next block is modified as follows:
Letting c be a counter, 0 for the first generated byte, and incremented by one as we change to use each additional generated byte, and letting n be the value of the current generated byte, we swap byte c and byte n of the next block.
This only requires the existence of a following block, and is therefore done when the current block is any block from the first through the nineteenth.
For each of the last 256 generated bytes of the 288 generated bytes we use in modifying the 256-byte current block, immediately following the use of that same byte for modifying the next block during the period when both operations overlap, we modify the preceding block as follows:
Letting c be a counter, 0 for the first generated byte used by this step, the 33rd of the 288 generated bytes for the current block, and letting n be the value of the current generated byte, we let p be the value of byte c of the next block, and let q be the value of byte n of the previous block.
We then swap bytes p and q of the previous block. Letting k be the XOR of the values of the two bytes so swapped, byte n of the previous block is then modified by being XORed with byte k of the next block.
This requires both a preceding and a following block, and is done for the second block through the nineteenth.
Performing these transposition steps on the subkey material helps to destroy any pattern it might contain.
As many of the last 2304 bytes of subkey material as required are used to generate a permutation following the steps used for generating the initial value of S8. The generated result, however, is not used as the final value of S8. Instead, each element of S8 is replaced by the value it points to in this result; that is, for N from 0 to 255, S8(N) becomes R(S8(N)). (Thus, S8 depends on both the old and new subkeys, and doesn't relate to the current subkeys in a simple way.)
Then, the 488 subkeys required for Quadibloc III are produced from the 440 subkeys generated normally and the 48 additional ones by using the 48 additional subkeys in order as the ones for the f-functions that are used to modify the f-function results before being XORed together in the Mishmash rounds.
Hence,
Note that implementations need not actually move the subkeys around, but merely need to ensure that each encipherment step uses the correct subkeys from those stored in memory.
Specific named variations of Quadibloc III are provided here to broaden its range of applicability.
The first variation is Quadibloc III SC (Short Cycle). This version retains the complexity of Quadibloc III, but eliminates the large number of rounds of the GoodStuff kind in the middle of the cipher. Instead, only two such rounds are retained, with the following arrangement:
1 > 2 > 3 > 4 > 5 > 6 > 7 > 8 8 < 7 < 6 < 5 < 4 < 3 < 2 < 1
This, by reducing the amount of required subkey material from 488 subkeys to 278, and hence the key augmentation phase of key generation is modified as follows: eight regular Quadibloc II rounds are used, the first 10 words of S10 are also modified, and there is no shifting of subkeys out of numerical order, as was required to exclude a particular 48 subkeys from key augmentation in the normal version. The unkeyed whitening step, and the initial and final byte transposes (0x and 8x) are also retained in the modified encipherment.
The next variation is Quadibloc III MD (Maximum Dispersion). This version adds eight 64-bit words of subkey material to what is used by the cipher. They are not used during the modified encipherment cycle performed for key augmentation, but they are generated initially, like other parts of the subkey material not then used. They are generated immediately after the 32 extra normal subkeys which are modified after, instead of during, key augmentation, and immediately before calculating S-box S8. Otherwise, since the key schedule is only lengthened, key augmentation is not otherwise modified for this variation.
These 64-bit words are used to perform an ICE-style interchange of the left and right halves of the block, immediately after the first four key-dependent byte interchanges derived from S-box S8 and immediately before the last four such byte interchanges. A 1 bit corresponds to a bit to be interchanged, and the words are used in order during encipherment.
Finally, Quadibloc III SD (Short/Dispersive) combines the modifications in Quadibloc III SC and Quadibloc III MD. As it has 294 32-bit words of normal subkey, the key augmentation phase of its key generation is based on a modified encipherment involving a byte transpose based on the 0x row of S8, an unkeyed whitening step, a set of four degenerate rounds, a byte transpose based on the 1x row of S8, eight normal Quadibloc II rounds, the 9x transpose, four degenerate rounds, inverse whitening, and the 8x transpose. The first two words of S10 are also included in the key augmentation for this variation.
A variation in the round structure, like those illustrated for Quadibloc II, will also be illustrated here, but in this case it is for the Mishmash portion of the cipher.
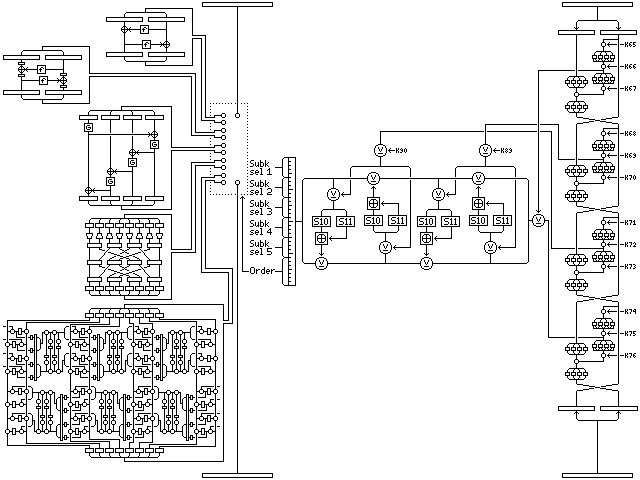
This diagram gives an overview of the Mishmash rounds as modified. Instead of placing the intermediate results of the four QUADIBLOC 96 rounds on the left side through an additional QUADIBLOC f-function, these results are used to produce a 32-bit result by means of the 32-bit Feistel structure used within the GoodStuff portion of the cipher. This reduces the number of additional subkeys required for this part of the cipher to 8 from 48, but the strength of the modified cipher appears fully satisfactory.
Another variation on Quadibloc III uses the modified Mishmash rounds described above, but in addition changes the order of the rounds in line with insights that have come out of looking at how some differential attacks, including the boomerang attack work. The idea is that parts of the cipher that are analytically simple are put on the outside, and parts that are harder to analyze, but possibly leaving room for new probing attacks, are put in the center. A diagram giving an overview of the variation, accompanied by its description, are below:
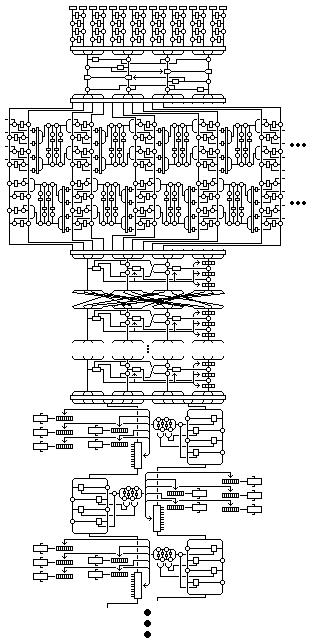
The 268 subkeys required, plus the first 20 32-bit words of the S-box S11, are modified after initial subkey generation by key augmentation through 32 normal Quadibloc II rounds with no degenerate rounds, (and two byte transposes, based on the 0x and 8x rows, instead of four, and two unkeyed whitening steps, as for the regular cipher) and there is no shifting of subkeys out of numerical order, as was required to exclude a particular 48 subkeys from key augmentation in the normal version.
The block cipher Quadibloc XI in this series has a secure key schedule which appears to me both efficient and secure. Quadibloc III RK (Revised Keys) may denote the variant which uses that key schedule as follows: generate the four bytes of each subkey in order, most significant (leftmost) first, generating the normal subkeys in simple numerical order from K1 to K488, and then use the method for generating a permutation to produce S8, and then generate the bytes of S10 and S11, and the subkey pools for the DES, 64-bit Quadibloc, SKIPJACK, SAFER and GoodStuff rounds in that order as for the regular key schedule for this cipher.
One modification is required, however; instead of using S3 as the S-box, one that is never used in the cipher itself is to be used; and the first one satisfying that criterion is the constant S-box produced from Euler's Constant listed on the page Euler's Constant and the Quadibloc S-boxes as S12, since the S5, S6, and S7 referred to on this page are (S5, S6), (S7, S8), and (S9, S10) as noted on that page, and the S-box denoted as S9 on this page is the one noted as S11 on that page.
For this method of subkey generation, the key must be a multiple of four bytes in length.
This revised form of subkey generation proceeds as follows:
Three strings of bytes of different length are produced from the key.
The first string consists of the key, followed by one byte containing the one's complement of the XOR of all the bytes of the key.
The second string consists of the one's complements of the bytes of the key in reverse order, with three bytes appended containing the following three quantities:
The third string consists of alternating bytes, taken from the bytes of the key in reverse order, and then from the bytes of the one's complement of the key, and then that string is followed by the one's complements of the first four bytes of the key.
Thus, if the key is:
128 64 32 16 8 4 2 1 1 2 3 4 5 6 7 8
then the strings generated from it are as follows:
First string: 128 64 32 16 8 4 2 1 1 2 3 4 5 6 7 8 8 Second string: 247 248 249 250 251 252 253 254 254 253 251 247 239 223 191 127 37 170 93 Third string: 8 127 7 191 6 223 5 239 4 247 3 251 2 253 1 254 1 254 2 253 4 252 8 251 16 250 32 249 64 248 128 247 127 191 223 239
Given that the length of the key is 4n, the lengths of the three strings are 4n+1, 4n+3, and 8n+4, and hence all three are relatively prime, since both 4n+1 and 4n+3 are odd, and 8n+4 is two times 4n+2.
Two buffers, each containing room for 256 bytes, are filled by generating bytes from the first and second strings by placing them in a nonlinear shift register.
The form of that shift register is shown in the following illustration, showing its precise form for the first string (but with S12 replaced by S3, as this is the diagram from the page on Quadibloc XI).
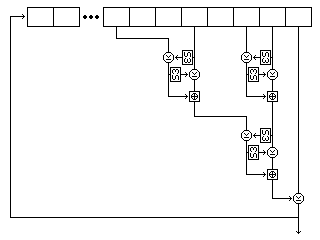
Five bytes are read from the string at each step. For the first string, they are, as shown in the diagram, the eighth-last, fifth-last, third-last, and second-last bytes and the last byte. For the second string, they are the eighth-last, seventh-last, fourth-last, and second-last bytes, and the last byte. For the third string, they are the twelfth-last, tenth-last, seventh-last, and fourth-last bytes, and the last byte.
Each time the shift register produces a byte, it does so as follows:
Both buffers contain 256 bytes. The first buffer, called buffer A, is filled with 256 successive bytes generated from the second string by means of the nonlinear shift register filled with the second string. The second buffer, called buffer B, is filled with 256 successive bytes generated from the first string by means of the nonlinear shift register filled with the first string.
Once the setup is complete, subkey material is generated one byte at a time, the first byte generated being the leftmost byte of subkey K1, and so on.
A subkey byte is generated as follows:
The following diagram attempts to illustrate the complete process of subkey byte generation (but with S-box S12 replaced by S-box S3, because it is the diagram from the page on Quadibloc XI):
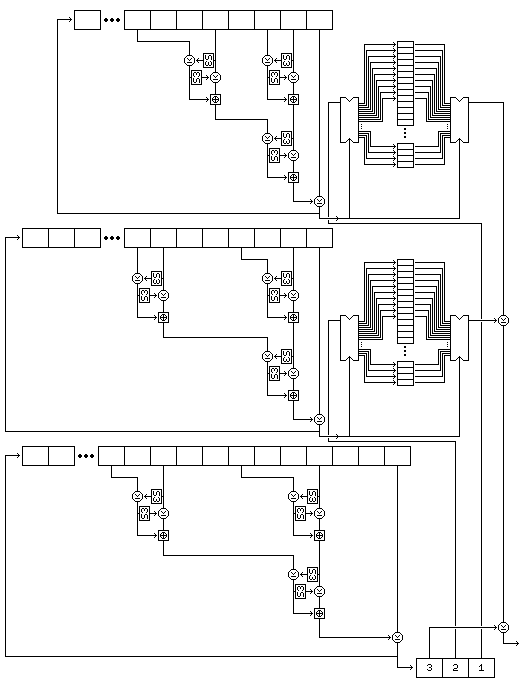
Note that this procedure, since it exercises the two strings used to select bytes, rather than the string used to generate values, results in a small change in the key resulting in large changes in the subkeys from the very beginning.
Once all the required 32-bit subkey words are generated, the key-dependent S-box S8 must be generated. To generate this bijective S-box, the following procedure is used:
The resulting contents of buffer D are used as the key-dependent bijective S-box intended to be produced.
This procedure, although it uses buffers A and B, leaves them undisturbed; thus, byte generation may continue after one S-box is produced.
Next
Start of Section
Skip to Next Chapter
Table of Contents
Main Page
Home Page