Quadibloc IV is a block cipher with a 128-bit blocksize with a simpler design than that of either Quadibloc III or even Quadibloc II. It has 32 rounds, numbered from 1 to 32, each using three 32-bit subkeys.
It uses the S-boxes S1, S2, and S3 (S3 is only used during key generation) derived from Euler's constant, as listed on the page entitled Euler's Constant and the Quadibloc S-Boxes.
It attempts - despite the fact that A xor B and B xor A are the same thing - to use a strategy derived from hash functions to produce a secure f-function; the quantity XORed to the first subblock in each round is the XOR of two f-functions, one which uses a subblock as input, and two subkeys as keys, and one which uses a subkey as input, and two subblocks as keys.
A round of Quadibloc IV proceeds as follows:
The 128-bit block is considered to be divided into four 32-bit subblocks, B1 through B4. The leftmost subblock, B1, is the only one modified in a round. It has two quantities XORed to it:
The f-function is essentially the basic Quadibloc f-function: XOR the input and the first key, substitute the bytes in the S-box, and then perform the following regular permutation of the bits:
1 2 27 28 21 22 15 16 9 10 3 4 29 30 23 24 17 18 11 12 5 6 31 32 25 26 19 20 13 14 7 8
Then, XOR the input and the second key and again perform the S and P steps. In Quadibloc IV, no third key is used.
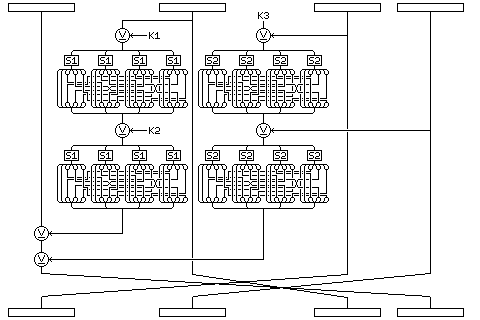
The following diagram illustrates a typical round of Quadibloc IV:

The diagram illustrates the way in which the subblocks are interchanged after a typical round:
3 4 2 1
No interchange is performed after the last round, round 32.
After round 4 and after round 28, the bytes of the 128-bit block are interchanged in the following order:
1 14 11 8 5 2 15 12 9 6 3 16 13 10 7 4
After round 16, the four subblocks are interchanged in this order:
3 2 1 4
After the other rounds whose numbers are divisible by 4, the four subblocks are interchanged in this order:
3 1 4 2
Hence, if one numbers the subblocks on entry to round 5 as 1, 2, 3, and 4, the orders in which they appear from round 5 to round 28 are as follows:
1 2 3 4 3 4 2 1 2 1 4 3 4 3 1 2 1 4 2 3 2 3 4 1 4 1 3 2 3 2 1 4 1 3 4 2 4 2 3 1 3 1 2 4 2 4 1 3 1 4 3 2 3 2 4 1 4 1 2 3 2 3 1 4 1 2 4 3 4 3 2 1 2 1 3 4 3 4 1 2 1 3 2 4 2 4 3 1 3 1 4 2 4 2 1 3
thus going through all 24 possible orders exactly once.
Because of the byte interchange after rounds 4 and 28, the first and last four rounds function as a whitening phase of the block cipher.
Two shift registers, one 64 bytes in length and one 65 bytes in length, are used to generate subkeys, and are loaded with the key, which can be from 2 to 63 bytes in length, as follows:
Initial values of subkey bytes are generated from these two shift registers as follows:
The first shift register is cycled as follows:
Take the 49th byte, add the 33rd byte, and XOR the 64th byte. Find the substitute for the result in S-box S3. XOR the 3rd byte, and add the 1st byte.
The result will be the new first byte of the shift register, the other bytes being advanced one place, and the old 64th byte being discarded.
The second shift register is cycled as follows:
Take the 23rd byte, add the 65th byte, and XOR the 11th byte. Find the substitute for the result in S-box S3. Add the 50th byte, and XOR the 1st byte.
The result will be the new 65th byte of the shift register, the other bytes being moved to the next earlier place, and the old 1st byte being discarded.
The byte of the subkey generated from this step is the generated new first byte of the first shift register, replaced with its substitute from S-box S3, XORed with the generated new 65th byte of the second shift register.
Once all 96 subkeys have been filled with their initial values, key augmentation takes place. A normal encipherment cycle is performed, enciphering the 128-bit block
A5 C3 E1 2D B4 87 96 F0 0F 69 78 4B D2 1E 3C 5A
but after each round, the four intermediate values generated in the round are applied as follows:
The four intermediate values are:
Intermediate values 1, 2, and 4 of each round are XORed to the subkeys after the round is over, and the order in which the subkeys is modified is:
K1 K4 K7 K10 K13 ... K94 K2 K5 K8 K11 K14 ... K95 K3 K6 K9 K12 K15 ... K96
and then, intermediate value 3 from the round is added, using byte-wide addition (as well as creating no endian confusion, this is sure to be implementable, even on systems that support only 16-bit arithmetic with no way to disable integer overflow exceptions) to the following subkeys in this order:
K96 K93 K90 K87 K84 ... K3
As this block cipher was designed using design principles from hash functions, it seemed appropriate to specify a mode in which it could be used to generate a hash of a file. However, only the simplest mode is specified here, generating a 128-bit hash, which is not considered adequately long to obtain collision resistance.
One iteration of the cipher will be used to hash a block consisting of 32 32-bit words, or 128 bytes. The string of bits to be hashed will be converted to a whole number of blocks by having a 1 appended to it, and then the result will be filled out with zeroes to fill the last block.
The starting value to be "enciphered" by the block cipher will be:
A5 C3 E1 2D B4 87 96 F0 0F 69 78 4B D2 1E 3C 5A
as used for key augmentation.
The subkeys for the encipherment will be supplied by the block to be hashed as follows:
Both subkeys
K3 K6 K9 K12 K15 ... K96
and subkeys
K95 K92 K89 K86 K83 ... K2
will be supplied from the bytes of the block, taken in groups of four, in order. (The first byte is the leftmost byte of the word.)
Subkeys
K1 K4 K7 K10 K13 ... K94
will be the following:
K1: 243F6A88 K4: 85A308D3 K7: 13198A2E K10: 03707344 K13: A4093822 K16: 299F31D0 K19: 082EFA98 K22: EC4E6C89 K25: 452821E6 K28: 38D01377 K31: BE5466CF K34: 34E90C6C K37: C0AC29B7 K40: C97C50DD K43: 3F84D5B5 K46: B5470917 K49: 9216D5D9 K52: 8979FB1B K55: D1310BA6 K58: 98DFB5AC K61: 2FFD72DB K64: D01ADFB7 K67: B8E1AFED K70: 6A267E96 K73: BA7C9045 K76: F12C7F99 K79: 24A19947 K82: B3916CF7 K85: 0801F2E2 K88: 858EFC16 K91: 636920D8 K94: 71574E69
which are the hexadecimal digits in the fractional portion of pi (also used as the starting value of the S-boxes and subkeys in Blowfish, although it uses 784 of them, not just 32 of them).
After each block is hashed, the input to the encryption cycle is XORed with the output to produce the current value of the hash, which will be the input to the next encryption cycle.
In Quadibloc IV ER (Extra Resistance), after generating the initial values of the subkeys, an additional 1536 to 2304 bytes are generated to create S8 in the same fashion as the initial value of S8 was generated in Quadibloc II and Quadibloc III. This key-dependent S-box is not modified again after key augmentation, and it is used to perform a substitution on the four bytes of the two f-function outputs after the second SP portion. This modification makes Quadibloc IV considerably more secure against differential and linear cryptanalysis.
The method used for generating subkeys for Quadibloc XI may be applied to this cipher as well, as it was applied to Quadibloc II and Quadibloc III. Here, S3 can be used as it was in Quadibloc XI, since in this cipher as well it is only used for key generation, either the normal kind, or this revised kind. For Quadibloc IV RK, subkeys K1 through K96 are generated, leftmost byte first, in numerical order by the method described below.
For this method of subkey generation, the key must be a multiple of four bytes in length.
Three strings of bytes of different length are produced from the key.
The first string consists of the key, followed by one byte containing the one's complement of the XOR of all the bytes of the key.
The second string consists of the one's complements of the bytes of the key in reverse order, with three bytes appended containing the following three quantities:
The third string consists of alternating bytes, taken from the bytes of the key in reverse order, and then from the bytes of the one's complement of the key, and then that string is followed by the one's complements of the first four bytes of the key.
Thus, if the key is:
128 64 32 16 8 4 2 1 1 2 3 4 5 6 7 8
then the strings generated from it are as follows:
First string: 128 64 32 16 8 4 2 1 1 2 3 4 5 6 7 8 8 Second string: 247 248 249 250 251 252 253 254 254 253 251 247 239 223 191 127 37 170 93 Third string: 8 127 7 191 6 223 5 239 4 247 3 251 2 253 1 254 1 254 2 253 4 252 8 251 16 250 32 249 64 248 128 247 127 191 223 239
Given that the length of the key is 4n, the lengths of the three strings are 4n+1, 4n+3, and 8n+4, and hence all three are relatively prime, since both 4n+1 and 4n+3 are odd, and 8n+4 is two times 4n+2.
Two buffers, each containing room for 256 bytes, are filled by generating bytes from the first and second strings by placing them in a nonlinear shift register.
The form of that shift register is shown in the following illustration, showing its precise form for the first string.
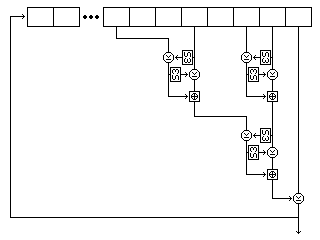
Five bytes are read from the string at each step. For the first string, they are, as shown in the diagram, the eighth-last, fifth-last, third-last, and second-last bytes and the last byte. For the second string, they are the eighth-last, seventh-last, fourth-last, and second-last bytes, and the last byte. For the third string, they are the twelfth-last, tenth-last, seventh-last, and fourth-last bytes, and the last byte.
Each time the shift register produces a byte, it does so as follows:
Both buffers contain 256 bytes. The first buffer, called buffer A, is filled with 256 successive bytes generated from the second string by means of the nonlinear shift register filled with the second string. The second buffer, called buffer B, is filled with 256 successive bytes generated from the first string by means of the nonlinear shift register filled with the first string.
Once the setup is complete, subkey material is generated one byte at a time, the first byte generated being the leftmost byte of subkey K1, and so on.
A subkey byte is generated as follows:
The following diagram attempts to illustrate the complete process of subkey byte generation:
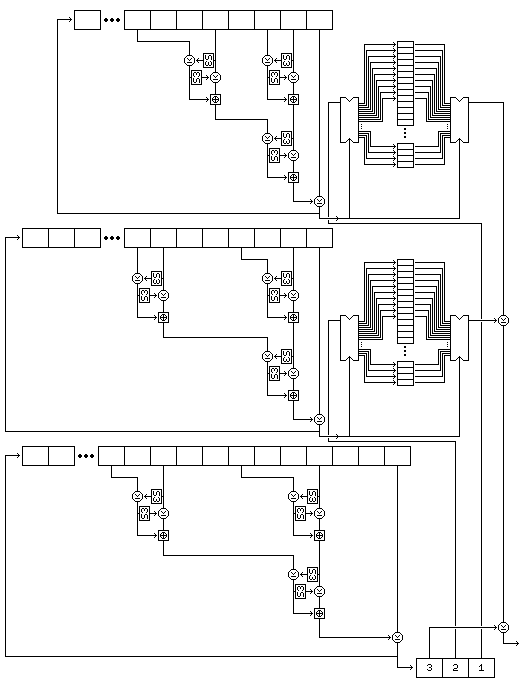
Note that this procedure, since it exercises the two strings used to select bytes, rather than the string used to generate values, results in a small change in the key resulting in large changes in the subkeys from the very beginning.
For Quadibloc IV ER RK, a key-dependent permutation S8 is required as well, and is generated after the subkeys are generated, using the same permutation generation method as described for Quadibloc IX:
The resulting contents of buffer D are used as the key-dependent bijective S-box intended to be produced. Note that this is a procedure, introduced for Quadibloc X, is more straightforwards than the other two basic procedures used previously to produce S8 in other ciphers in this series.
This procedure, although it uses buffers A and B, leaves them undisturbed; thus, byte generation may continue after one S-box is produced.
Next
Start of Section
Skip to Next Chapter
Skip to Next Section
Table of Contents
Main Page
Home Page