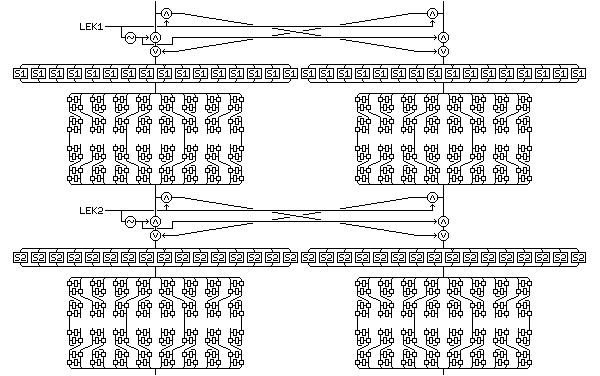
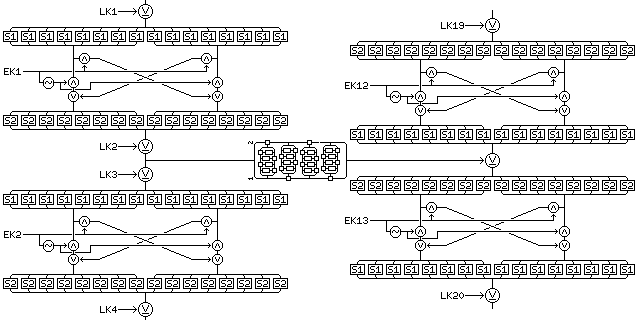
Quadibloc XIX

Quadibloc XIX is a block cipher with a 256-bit block size formed from components introduced in the description of the block cipher Quadibloc 2002E and its variants.

It consists of an initial mixing phase, followed by the cipher proper, and a final mixing phase.

The initial mixing phase consists of the following operations:

• Bits are swapped between 128-bit halves of the block under control of the 128-bit exchange key LEK1.
• Bytes are replaced with their substitutes in self-inverse S-box S1.
• Each half of the block undergoes a lesser diffusion phase.
• Bits are swapped between 128-bit halves of the block under control of the 128-bit exchange key LEK2.
• Bytes are replaced with their substitutes in self-inverse S-box S2.
• Each half of the block undergoes a lesser diffusion phase.
• Bits are swapped between 128-bit halves of the block under control of the 128-bit exchange key LEK3.
• Bytes are replaced with their substitutes in self-inverse S-box S1.
• Each half of the block undergoes a lesser diffusion phase.
• Bits are swapped between 128-bit halves of the block under control of the 128-bit exchange key LEK4.
• Bytes are replaced with their substitutes in self-inverse S-box S2.
• Each half of the block undergoes a lesser diffusion phase.
• Bits are swapped between 128-bit halves of the block under control of the 128-bit exchange key LEK5.

The final mixing phase operates in the same manner, except that long exchange keys LEK6 through LEK10 are used, the S-boxes are used in the order S2, S1, S2, S1, and the lesser diffusion phases precede, rather than follow, the nonlinearity phases using those S-boxes.

These lesser diffusion phases use bijective S-boxes designated SB30 and SB31, rather than using SB3 and SB4 as do the lesser diffusion phases in the main part of the cipher.

The following diagram, showing the lesser diffusion phases schematically, but the rest in normal scale, shows the first two layers of the mixing phase:

The main part of the cipher consists of an encipherment of the two halves of the block by a series of operations somewhat similar to those found in Quadibloc 2002EA SR. (Note that the left half of the block uses the opposite ordering convention as in that cipher, instead of using the same ordering and leaving the opposite ordering for the right half. This has no effect on the strength of the cipher, and was thus not altered when it was noticed.) The two halves of the block also interact, using the main part of the core round f-function of Quadibloc 2002E, excluding the entry and exit bit swaps, and including the four Feistel rounds only, to take as input an intermediate value of one half of the block, and provide an output which is then applied by means of an XOR to the other half of the block.

Instead of reversing the order of alternation between the three types of diffusion phase halfway through the cipher, the left half of the block undergoes diffusion phases in the order:

• Greater Diffusion Phase (as introduced in Quadibloc 2002EM)
• Lesser Diffusion Phase (as introduced in Quadibloc 2002EC)
• Compound Diffusion Phase (as introduced in Quadibloc 2002EA)

throughout the cipher, and the right half of the block undergoes diffusion phases in the reverse order throughout the cipher. As can be seen from the list above, the most advanced forms of these phases, as used in Quadibloc 2002EA, are used in all three cases.

The greater diffusion phase, as used in this cipher, has this form:

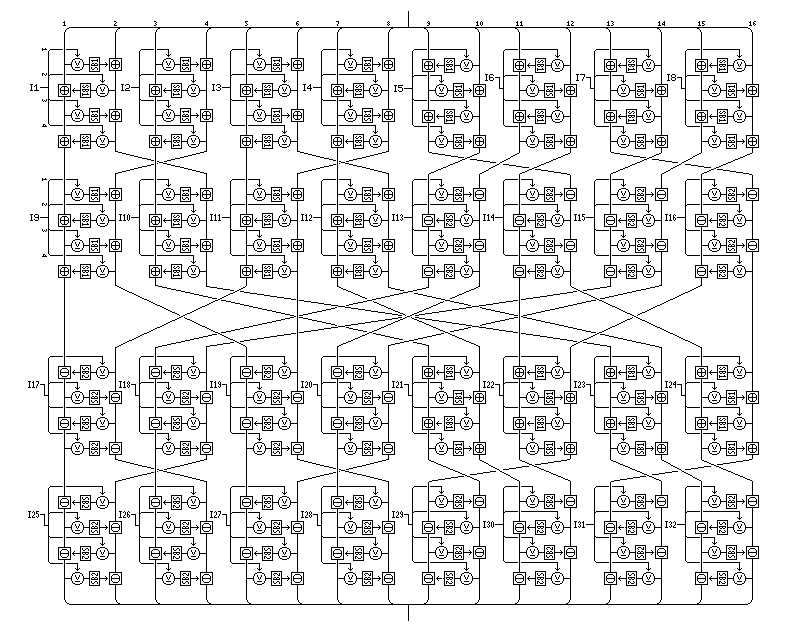
and the lesser diffusion phase is the one contained in this diagram (also showing other parts of Quadibloc 2002E):

and the compound diffusion phase looks like this:

Each half of the block undergoes seven diffusion phases. Both halves of the block can be considered as undergoing a diffusion phase at the same time; the order is:

     Left          Right
     --------      --------
1)   Greater       Greater
2)   Lesser        Compound
3)   Compound      Lesser
4)   Greater       Greater
5)   Lesser        Compound
6)   Compound      Lesser
7)   Greater       Greater

if this was not completely clear from the above description.

Between the first and second, the third and fourth, and the fifth and sixth pairs of diffusion phases, the left half of the block modifies the right half of the block by means of the following operations:

• On the left half of the block:
  • A key phase is performed on the left half of the block.
  • A nonlinearity phase (using S1) is performed on the left half of the block.
  • A bit swap phase is performed on the left half of the block.
  • An alternate nonlinearity phase (using S2) is performed on the left half of the block.
  • A key phase is performed on the left half of the block.
  • The value of the left half of the block at this point is taken as the input to the four Feistel rounds which form the main part of the core round f-function from Quadibloc 2002E.
  • A key phase is performed on the left half of the block.
  • A nonlinearity phase (using S1) is performed on the left half of the block.
  • A bit swap phase is performed on the left half of the block.
  • An alternate nonlinearity phase (using S2) is performed on the left half of the block.
  • A key phase is performed on the left half of the block.
• On the right half of the block:
  • A key phase is performed on the right half of the block.
  • An alternate nonlinearity phase (using S2) is performed on the right half of the block.
  • A bit swap phase is performed on the right half of the block.
  • A nonlinearity phase (using S1) is performed on the right half of the block.
  • The right half of the block is modified by being XORed with the output of the four Feistel rounds which form the main part of the core round f-function from Quadibloc 2002E.
  • An alternate nonlinearity phase (using S2) is performed on the right half of the block.
  • A bit swap phase is performed on the right half of the block.
  • A nonlinearity phase (using S1) is performed on the right half of the block.
  • A key phase is performed on the right half of the block.

Between the second and third, the fourth and fifth, and the sixth and seventh pairs of diffusion phases, the right half of the block modifies the left half of the block by means of the following operations:

• On the right half of the block:
  • A key phase is performed on the right half of the block.
  • An alternate nonlinearity phase (using S2) is performed on the right half of the block.
  • A bit swap phase is performed on the right half of the block.
  • A nonlinearity phase (using S1) is performed on the right half of the block.
  • A key phase is performed on the right half of the block.
  • The value of the right half of the block at this point is taken as the input to the four Feistel rounds which form the main part of the core round f-function from Quadibloc 2002E.
  • A key phase is performed on the right half of the block.
  • An alternate nonlinearity phase (using S2) is performed on the right half of the block.
  • A bit swap phase is performed on the right half of the block.
  • A nonlinearity phase (using S1) is performed on the right half of the block.
  • A key phase is performed on the right half of the block.
• On the left half of the block:
  • A key phase is performed on the left half of the block.
  • A nonlinearity phase (using S1) is performed on the left half of the block.
  • A bit swap phase is performed on the left half of the block.
  • An alternate nonlinearity phase (using S2) is performed on the left half of the block.
  • The left half of the block is modified by being XORed with the output of the four Feistel rounds which form the main part of the core round f-function from Quadibloc 2002E.
  • A nonlinearity phase (using S1) is performed on the left half of the block.
  • A bit swap phase is performed on the left half of the block.
  • An alternate nonlinearity phase (using S2) is performed on the left half of the block.
  • A key phase is performed on the left half of the block.

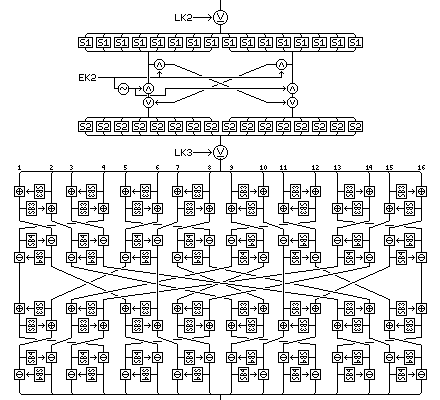
What takes place between the first and second diffusion phases is illustrated by the following diagram, in which the f-function of the overall Feistel round, which is composed of the same four rounds as described on one of the pages within the description of Quadibloc 2002E, is noted only by a small diagram at a high overview level, (this page shows some rounds of Quadibloc 2002E, including the full four rounds used again here as an f-function, at the more normal overview level also used below in some diagrams for diffusion phases; the size of that diagram will illustrate why this f-function is difficult to depict normally) but in which the operations directly between diffusion phases are drawn normally:

Following these six in-place Feistel rounds taking place in between seven pairs of diffusion phases, and preceding the final mixing phase, the 128-bit halves of the block are swapped, in order to give this cipher a symmetric structure allowing decryption to be performed by means of changes to the key schedule only. The diagram on the right may make the rationale behind this clearer.

A diagram showing a somewhat larger portion of this cipher may be useful in making the description above somewhat more clear:

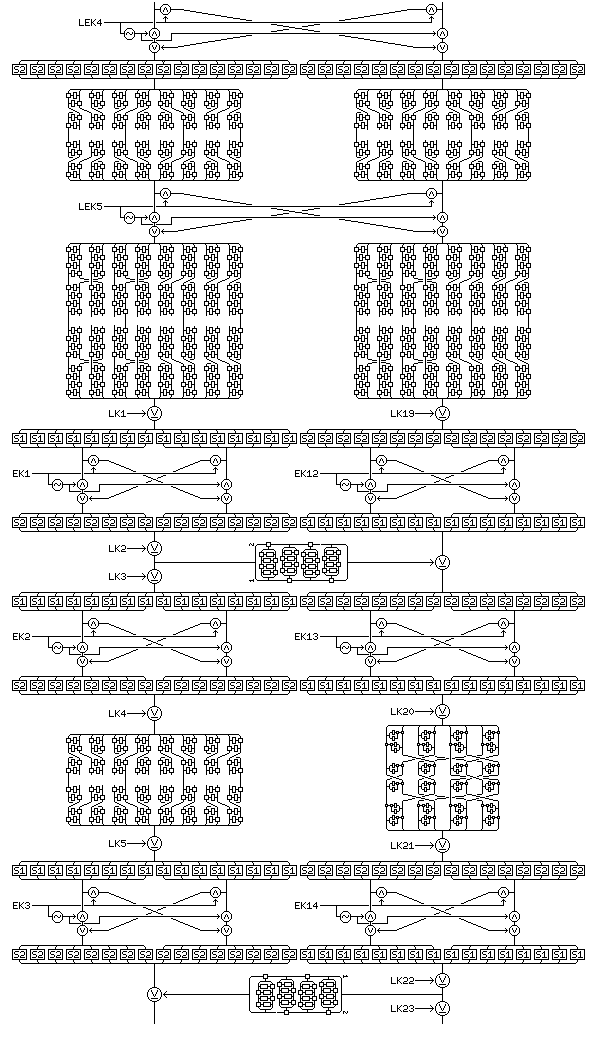
The principle behind the design of this cipher is to obtain strength by a balance between the number of rounds and the complexity of each round, on the theory that several complex rounds are stronger than either many simple rounds or few very complex rounds. Also, the initial and final mixing phases, combined with the double bit swap phases between diffusion phases, and the use of the sequence of diffusion phases from Quadibloc 2002EA, are intended to make the path of each bit through the cipher uncertain.

However, it could be considered a weakness of this cipher that all the bit swap phases are only key-dependent, and not data-dependent. The new type rounds in Quadibloc 2002E U have data-dependent bit swaps within the f-function, but not data-dependent bit swaps in the direct data path; in that cipher, the new type rounds have data-dependent algorithmic variability, the standard rounds have key-dependent algorithmic variability, and the core rounds have a fixed, but very involved, algorithm. The algorithmic variability consists of changing the path bits take through an otherwise fixed algorithm, to prevent vulnerability to timing attacks.

The Key Schedule

The key schedule consists of the following elements, listed in the order of their generation:

Ten long exchange keys, LEK1 to LEK10, each one 128 bits in length, and produced from 128 bits of key material by means of the 4 of 8 code noted for the purpose of producing exchange keys of all sizes in the description of Quadibloc 2002E.

Two bijective S-boxes, SB30 and SB31, each one containing a permutation of the 256 values from 0 to 255, for use in the lesser diffusion phases in the initial and final mixing phases of the cipher.

Ninety-six subkeys, K1 to K96, each one 32 bits in length, for use in the greater diffusion phases enciphering the left half of the block.

Ninety-six subkeys, K97 to K192, each one 32 bits in length, for use in the greater diffusion phases enciphering the right half of the block.

Two bijective S-boxes, SB1 and SB2, each one containing a permutation of the 256 values from 0 to 255, for use in the greater diffusion phases.

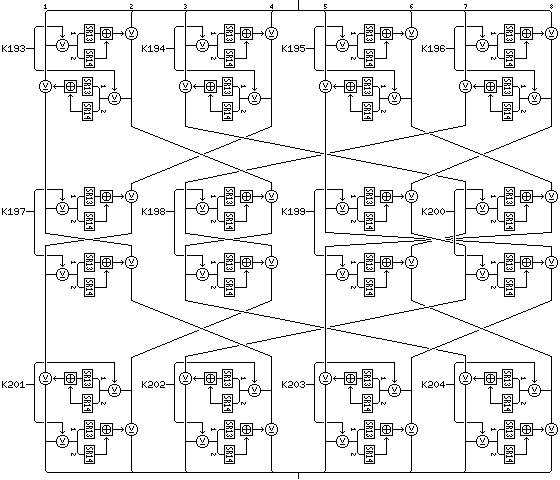
Twenty-four subkeys, K193 to K216, each one 32 bits in length, for use in the compound diffusion phases enciphering the left half of the block.

Twenty-four subkeys, K217 to K240, each one 32 bits in length, for use in the compound diffusion phases enciphering the right half of the block.

Two random S-boxes, SR13 and SR14, each one containing 256 entries, each of which is 16 bytes in length, and which are otherwise unrestricted, being derived directly from key material, for use in compound diffusion phases.

Two bijective S-boxes, SB3 and SB4, each one containing a permutation of the 256 values from 0 to 255, for use in the lesser diffusion phases.

Twelve exchange keys, EK1 to EK12, each one 64 bits in length, for use in the encipherment of the left half of the block, and produced from 64 bits of key material by means of the 4 of 8 code noted for this purpose in the description of Quadibloc 2002E.

Twelve exchange keys, EK13 to EK24, each one 64 bits in length, for use in the encipherment of the right half of the block, and produced from the 4 of 8 code noted above.

Eighteen long subkeys, LK1 to LK18, each one 128 bits in length, used in the encipherment of the left half of the block.

Eighteen long subkeys, LK19 to LK36, each one 128 bits in length, used in the encipherment of the right half of the block.

One hundred and ninety-two subkeys, K241 to K432, each one 32 bits in length, for use in the f-function of the six overall Feistel rounds in this cipher, used in the order of the rounds, whether from left to right or right to left.

Six bijective S-boxes, SB6 to SB11, each one containing a permutation of the 256 values from 0 to 255, for use in the f-function of the overall Feistel rounds.

Two random S-boxes, SR1 and SR2, each one containing 256 entries, each of which is 16 bytes in length, for use in the f-function of the overall Feistel rounds.

The 4-of-8 code to be applied to the least significant (rightmost) six bytes of each byte used to produce the exchange keys is as follows:

55 56 59 5A 65 66 69 6A 95 96 99 9A A5 A6 A9 AA
35 36 39 3A C5 C6 C9 CA 53 5C 63 6C 93 9C A3 AC
4D 4E 71 72 8D 8E B1 B2 17 1B 27 2B D4 D8 E4 E8
1D 1E 2D 2E D1 D2 E1 E2 47 4B 74 78 87 8B B4 B8

The key material is produced using the same generator and setup procedure as for Quadibloc 2002E, as described and illustrated below.

The positions of the buffers A through D in the diagram above are as follows:

C A
D B

and the steps involved in the procedure as illustrated are:

Initialization

Three strings of bytes of different length are produced from the key.

The first string consists of the key, followed by one byte containing the one's complement of the XOR of all the bytes of the key.

The second string consists of the one's complements of the bytes of the key in reverse order, with three bytes appended containing the following three quantities:

• The sum, modulo 255, of the bytes of the key, incremented by one by normal addition. (Thus, this produces a number from 1 to 255.)
• The XOR of all the bytes at odd numbered positions in the key, where the first byte in the key is considered to be byte 1, and odd.
• The one's complement of the XOR of all the bytes at even numbered positions in the key.

The third string consists of alternating bytes, taken from the bytes of the key in reverse order, and then from the bytes of the one's complement of the key, and then that string is followed by the one's complements of the first four bytes of the key.

Thus, if the key is:

 128  64  32  16   8   4   2   1   1   2   3   4   5   6   7   8

then the strings generated from it are as follows:

First string:
 128  64  32  16   8   4   2   1
   1   2   3   4   5   6   7   8
   8

Second string:
 247 248 249 250 251 252 253 254
 254 253 251 247 239 223 191 127
  37 170  93

Third string:
   8 127   7 191   6 223   5 239
   4 247   3 251   2 253   1 254
   1 254   2 253   4 252   8 251
  16 250  32 249  64 248 128 247
 127 191 223 239

Given that the length of the key is 4n, the lengths of the three strings are 4n+1, 4n+3, and 8n+4, and hence all three are relatively prime, since both 4n+1 and 4n+3 are odd, and 8n+4 is two times 4n+2.

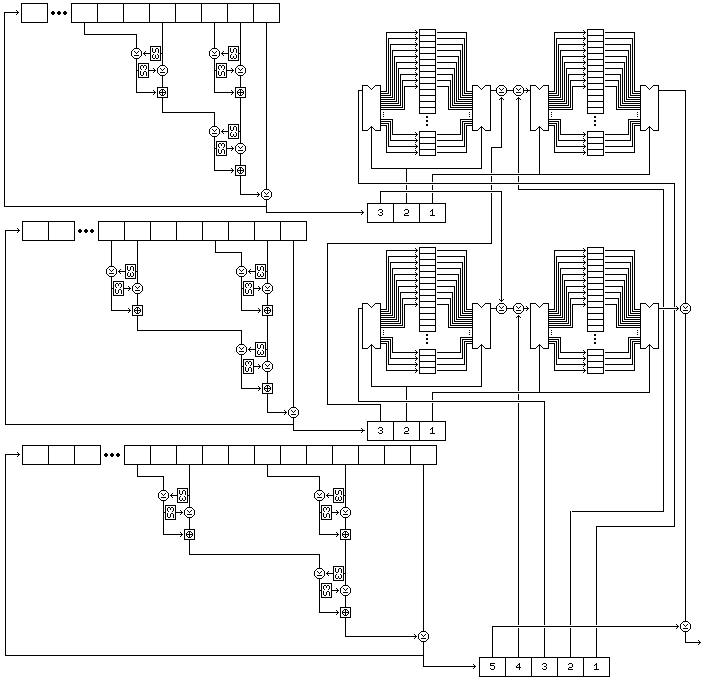
Two buffers, each containing room for 256 bytes, are filled by generating bytes from the first and second strings by placing them in a nonlinear shift register.

The form of that shift register is shown in the following illustration, showing its precise form for the first string.

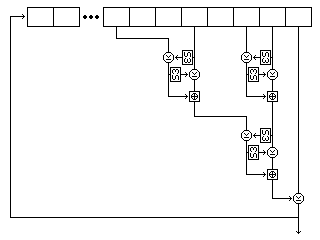
Five bytes are read from the string at each step. For the first string, they are, as shown in the diagram, the eighth-last, fifth-last, third-last, and second-last bytes and the last byte. For the second string, they are the eighth-last, seventh-last, fourth-last, and second-last bytes, and the last byte. For the third string, they are the twelfth-last, tenth-last, seventh-last, and fourth-last bytes, and the last byte.

Each time the shift register produces a byte, it does so as follows:

• The second byte read is used to select an entry in S-box S3, and the value of this entry is XORed to the first byte. Then the first byte is used to select an entry in S-box S3, and the value of this entry is XORed to the second byte.
• The fourth byte read is used to select an entry in S-box S3, and the value of this entry is XORed to the third byte. Then the third byte is used to select an entry in S-box S3, and the value of this entry is XORed to the fourth byte.
• The first and second bytes, as modified, are added together using modulo-256 addition to form a first result.
• The third and fourth bytes, as modified, are added together using modulo 256 addition to form a second result.
• The second result is used to select an entry in S-box S3, and the value of this entry is XORed to the first result. Then the first result is used to select an entry in S-box S3, and the value of this entry is XORed to the second result.
• The two results as modified are added together using modulo 256 addition to form a third result.
• The fifth byte read, which is always the last byte in the shift register, is XORed with the third result. The resulting value is output as the byte produced by operating the shift register.
• The values in the shift register are modified by removing the last byte, advancing the bytes in the shift register to the next later position, and appending the output result as the new first byte of the shift register contents.

The cipher uses four buffers, each of which contain 256 bytes. The first buffer, called buffer A, is filled with 256 successive bytes generated from the second string by means of the nonlinear shift register filled with the second string, and then buffer C is filled with another 256 bytes generated from the second string. The second buffer, called buffer B, is filled with 256 successive bytes generated from the first string by means of the nonlinear shift register filled with the first string, and then buffer D is filled with another 256 bytes generated from the first string.

Subkey Byte Generation

• Three bytes are generated from the first string by its associated nonlinear shift register operation, and they will be called U, V, and W in order.
• Three bytes are generated from the second string by its associated nonlinear shift register operation, and they will be called F, G, and H in order.
• Five bytes are generated from the third string by its associated nonlinear shift register operation, and they will be called J, K, L, M, and N in order.
• The byte at the position in buffer A indicated by the value U is taken, and called P.
• The byte at the position in buffer C indicated by the value V is taken, and it is XORed with both the value H and the value K, and the result is placed in buffer A, at the position indicated by the value U, replacing the value taken from the buffer A.
• The byte at the position in buffer B indicated by the value F is taken, and called Q.
• The byte at the position in buffer D indicated by the value G is taken, and it is XORed with both the value W and the value M, and the result is placed in buffer B, at the position indicated by the value F, replacing the value taken from the buffer B.
• The value J is placed in buffer C, replacing the value taken from that buffer, by being placed at the location indicated by the value V.
• The value L is placed in buffer D, replacing the value taken from that buffer, by being placed at the location indicated by the value G.
• The subkey byte generated is the XOR of P and Q and N.

Permutation Generation

To generate bijective S-boxes, which in the case of this cipher are the S-boxes SB1 through SB16, the following procedure is used:

• 256 bytes are generated following the same procedure as for subkey byte generation, and these bytes are placed in a 256-byte buffer called buffer C.
• A 256-byte buffer called buffer D is filled with the numbers from 0 to 255 in order.
• For every i from 0 to 255, if element i of buffer C (hereinafter called C(i)) is not equal to i, swap elements i and C(i) of buffer D.
• For every i from 0 to 255, if B(i) is not equal to i, swap elements i and B(i) of buffer D.
• For every i from 0 to 255, if A(i) is not equal to i, swap elements i and A(i) of buffer D.

The resulting contents of buffer D are used as the key-dependent bijective S-box intended to be produced. Note that this is a procedure, introduced for Quadibloc X, is more straightforwards than the other two basic procedures used previously to produce S8 in other ciphers in this series.

This procedure, although it uses buffers A and B, leaves them undisturbed; thus, byte generation may continue after one S-box is produced.

Long Keys

The subkey generation procedure given above works well for keys from 64 bits to 1,024 bits in length. When the length of the key approaches 2,048 bits in length, however, the first two shift registers are no longer thoroughly mixed by filling the buffers initially.

Thus, the following modified subkey generation procedure is given for keys which are more than 1,024 bits long. A key must still be a multiple of 32 bits in length.

• (1) Divide the key into blocks of 512 bits until the remaining part of the key is from 512 to 992 bits in length.
• (2) Use the first block of the key as the key for the normal Quadibloc 2002E key schedule.
• (3) Continue to generate enough additional subkey bytes to XOR these with the next block into which the key was divided.
• (4) Use the next block, after the XOR, to carry out the Quadibloc XIX key schedule except:
  • Exclude the exchange keys (EK1 ... EKn) and the long exchange keys (LEK1 ... LEKn) as well entirely from generation;
  • The subkey material generated is XORed with the previously generated values of the subkeys in the case of subkeys of any length (K1 ... Kn, LK1 ... LKn) and of S-boxes with random contents (SR1 ... SRn);
  • When using the second block, and any even-numbered block, generate the contents of SR1 and SR2 first rather than last, leaving the order of key generation otherwise unchanged;
  • Generate permutations for the bijective S-boxes (SB1 ... SBn) in the normal sequence of generation, and then modify the bijective S-boxes to be used in the cipher as follows: go through the newly-generated bijective S-boxes and the previously calculated bijective S-boxes from positions 0 to 255; in a new array, place the value in the new permutation in the position indicated by the value in the original permutation. Once this is finished, the new array is the replacement permutation.
• (5) If there are any additional blocks remaining in the key, go back to step 3.

This method ensures that the key schedule is a function of the entire key.

Decipherment

For decipherment, S-boxes SB1 and SB2 are swapped, as are S-boxes SB3 and SB4 and S-boxes SB30 and SB31; otherwise, all S-boxes remain unchanged. The changes made to other subkeys are obvious from their purpose, and follow the same basic plan as in Quadibloc 2002E and its variants:

The order of subkeys LEK1 through LEK10 is reversed.

The order of subkeys K1 through K192, taken in groups of thirty-two, is reversed, with each group retaining its order, and with the four bytes within each subkey also being reversed in order.

The order of subkeys K193 through K240, taken in groups of four, is reversed, with each group retaining its order.

The order of subkeys EK1 through EK24 is reversed.

The order of subkeys LK1 through LK36 is reversed.

The order of subkeys K241 through K432, taken in groups of thirty-two, is reversed, with each group retaining its order.

Note that there are no exchange keys the bits of which must be inverted in order to effect decipherment in this cipher, following the method used within Quadibloc 2002E, where the main f-function, the input and output of which came from, or entered into, respectively, steps separated in time, had to be guarded by extra bit swaps in order to achieve the possibility of reversing the cipher by key schedule changes. Also note that the reversals of subkeys in the groups K1 through K192, K193 through K240, EK1 through EK24, and LK1 through LK36, leads to the keys being used for the left half of the block being used for the right half of the block on decipherment; this is correct, and is a consequence of the swap of halves of the block at the end of the main part of the cipher.

Variants

If it is felt that six main Feistel rounds are inadequate for this cipher, it is easy to increase the number of rounds to twelve while maintaining the symmetry of the cipher. It is possible to use intermediate even numbers of main Feistel rounds as well, through a suitable choice of diffusion phase types in the main part of the cipher. For example, for eight rounds, the sequence would be:

     Left          Right
     --------      --------
1)   Greater       Compound
2)   Lesser        Lesser
3)   Compound      Greater
4)   Greater       Compound
5)   Lesser        Lesser
6)   Compound      Greater
7)   Greater       Compound
8)   Lesser        Lesser
9)   Compound      Greater

so that the sequence of diffusion phase types from the beginning for the left half is the same as the sequence from the end for the right half.

To introduce data-dependent bit swaps into the cipher, the operations between pairs of diffusion phases which constitute the main overall Feistel rounds of this cipher can be modified in some cases to the following:

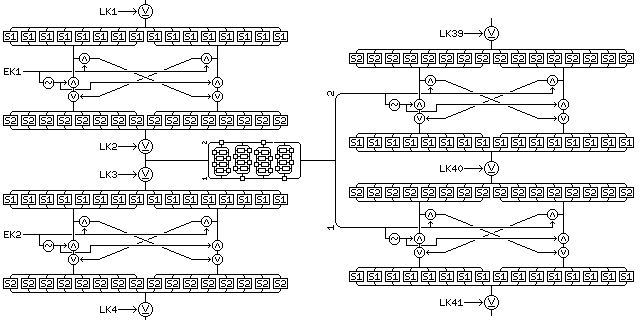
This illustration shows the first overall Feistel round from a 12-round variant of Quadibloc XIX, to be known as Quadibloc XIX DR (Data-dependent Redirection). The modification it shows, using the f-function output as the source of the two exchange keys for the bit swap phases between diffusion phases rather than as the source of one of the long keys for the central key phase between diffusion phases, is applied to the first, second, eleventh, and twelfth rounds. This increases the number of required long keys by four, and decreases the number of required exchange keys by eight, as compared to a plain 12-round variant.

Symmetry between encipherment and decipherment is maintained by using the right half of the f-function output first, as shown in the diagram, in the first and eleventh rounds, when the Feistel round operates from left to right, and using the left half of the f-function output first when the Feistel round operates from right to left, in the second and twelfth rounds.

As this has the incidental effect of making schematic diagrams of the cipher easier to draw, it increases security. This is because people implementing the cipher to protect their data must test it to ensure that decryption genuinely produces the same output as was originally given as input to encryption. People attempting to understand the cipher for purposes of cryptanalysis, on the other hand, might assume that this property was an erroneous result of laziness on the part of a draughtsman. Actually, of course, increased security is not obtained by a trick like this except in the case of a cipher whose algorithm is kept secret.

Although the preceding paragraph does communicate a useful idea, some of its literal content, particularly in the earlier sentences, was structured with humorous intent.

The key material required by this variant is therefore:

• LEK1 to LEK10 (mixing phase)
• SB30 and SB31 (lesser diffusion phases in mixing phase)
• K1 to K320 (greater diffusion phases)
• SB1 and SB2 (greater diffusion phases)
• K321 to K416 (compound diffusion phases)
• SR13 and SR14 (compound diffusion phases)
• SB3 and SB4 (lesser diffusion phases, main cipher)
• EK1 to EK40 (main cipher)
• LK1 to LK76 (main cipher)
• K417 to K800 (f-function, main cipher)
• SB6 to SB11 (f-function, main cipher)
• SR1 and SR2 (f-function, main cipher)

and the changes required for decipherment are the same as for regular Quadibloc XIX, but applied to the key material having similar functions.

Next
Start of Section
Skip to Next Chapter
Skip to Next Section
Table of Contents
Main Page