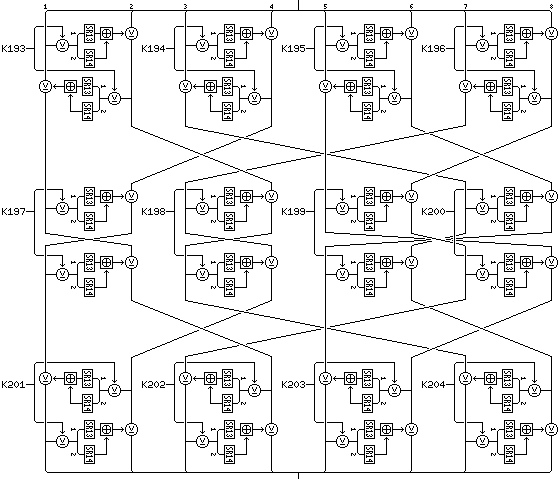
This section deals with a modification of Quadibloc 2002E that is applicable to all variants which make use of the standard rounds. It consists of the introduction of a third form of the diffusion phase, as illustrated in the diagram below:

In the first half of the cipher for most variants, or in the first half of any symmetric group of standard rounds in the variants operating on 256-bit blocks, the modification to the cipher is that whenever a standard round using a greater diffusion phase is immediately followed by a standard round using a lesser diffusion phase, a standard round using a diffusion phase of the type illustrated above, referred to as a compound diffusion phase, is inserted. In the second half of the cipher, or in the second half of the symmetric groups of standard rounds in variants with a 256-bit block, the order of round types is reversed, and thus a standard round using a compound diffusion phase is inserted following a standard round using a lesser diffusion phase which immediately preceded a standard round using a greater diffusion phase.
In the case of 128-bit block ciphers, this insertion will increase the total number of rounds. In most cases of 256-bit block ciphers, because of their structure, the number of rounds will remain constant, and the insertion of rounds with compound diffusion phases will simply modify the sequence of round types. The exceptions to this are Quadibloc 2002EA WU and Quadibloc 2002EA WR, where in each of the four segments, the number of standard rounds and the number of core rounds shall each increase from four to six, in order to ensure that all three types of standard round shall continue to be represented.
The greater and lesser diffusion phases shall be as modified for Quadibloc 2002EM.
In the compound diffusion phase, there are three layers of operations, each involving four Feistel rounds, acting on 32-bit blocks composed of two 16-bit halves.
Between the first and second layers, and between the second and third layers, 16-bit segments are transposed to the order:
1 4 7 2 5 8 3 6
and, in addition, in the middle of the second layer, the halves of the first two 32-bit blocks are swapped, and the order of the four 16-bit segments in the second half of the block is reversed.
This leads to the 16-bit segments of the block being transposed to the order:
4 7 8 1 6 5 2 3
which, when expressed in terms of bytes, becomes the arrangement:
7 8 13 14 15 16 1 2 11 12 9 10 3 4 5 6
Note that this arrangement of three layers, to maintain symmetry but deal in only 16-bit segments, has the limitation that each 32-bit subblock is connected to itself and two of the three other subblocks, rather than providing complete diffusion.
That of the lesser diffusion phase is to the order:
6 12 14 4 15 1 7 9 8 10 16 2 13 3 5 11
and that of the greater diffusion phase is to the order:
1 14 10 5 4 15 11 8 16 3 7 12 13 2 6 9
Thus, the net effect of three standard rounds followed by an additional bit swap phase can be determined:
Once again, in the beginning, the bytes are independent:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
After the first bit swap phase, they are mixed as follows:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 9 10 11 12 13 14 15 16 1 2 3 4 5 6 7 8
where, under the number of each byte, is the number, in the original ordering, of the other byte with which it has swapped bits.
After a greater diffusion phase, the ordering of the bytes is changed to this:
1 14 10 5 4 15 11 8 16 3 7 12 13 2 6 9 9 6 2 13 12 7 3 16 8 11 15 4 5 10 14 1
Then, the second bit swap phase causes further mixing, so that the bytes now include bits from other bytes as shown here:
1 14 10 5 4 15 11 8 16 3 7 12 13 2 6 9 9 6 2 13 12 7 3 16 8 11 15 4 5 10 14 1 16 3 7 12 13 2 6 9 1 14 10 5 4 15 11 8 8 11 15 4 5 10 14 1 9 6 2 13 12 7 3 16
The compound diffusion phase then re-orders these mixed bytes so that they stand in the following order:
11 8 13 2 6 9 1 14 7 12 16 3 10 5 4 15 3 16 5 10 14 1 9 6 15 4 8 11 2 13 12 7 6 9 4 15 11 8 16 3 10 5 1 14 7 12 13 2 14 1 12 7 3 16 8 11 2 13 9 6 15 4 5 10
and the following bit swap phase mixes these bytes further so that the sources for each byte are now as given below:
11 8 13 2 6 9 1 14 7 12 16 3 10 5 4 15 3 16 5 10 14 1 9 6 15 4 8 11 2 13 12 7 6 9 4 15 11 8 16 3 10 5 1 14 7 12 13 2 14 1 12 7 3 16 8 11 2 13 9 6 15 4 5 10 7 12 16 3 10 5 4 15 11 8 13 2 6 9 1 14 15 4 8 11 2 13 12 7 3 16 5 10 14 1 9 6 10 5 1 14 7 12 13 2 6 9 4 15 11 8 16 3 2 13 9 6 15 4 5 10 14 1 12 7 3 16 8 11
Then, the rearrangement performed within the lesser diffusion phase reorders these bytes to the following sequence:
9 3 5 2 4 11 1 7 14 12 15 8 10 13 6 16 1 11 13 10 12 3 9 15 6 4 7 16 2 5 14 8 8 14 12 15 13 6 16 10 3 5 2 9 7 4 11 1 16 6 4 7 5 14 8 2 11 13 10 1 15 12 3 9 5 2 9 3 1 7 4 11 15 8 14 12 6 16 10 13 13 10 1 11 9 15 12 3 7 16 6 4 14 8 2 5 12 15 8 14 16 10 13 6 2 9 3 5 11 1 7 4 4 7 16 6 8 2 5 14 10 1 11 13 3 9 15 12
and, finally, one further bit swap now results in each byte having the sources:
9 3 5 2 4 11 1 7 14 12 15 8 10 13 6 16 1 11 13 10 12 3 9 15 6 4 7 16 2 5 14 8 8 14 12 15 13 6 16 10 3 5 2 9 7 4 11 1 16 6 4 7 5 14 8 2 11 13 10 1 15 12 3 9 5 2 9 3 1 7 4 11 15 8 14 12 6 16 10 13 13 10 1 11 9 15 12 3 7 16 6 4 14 8 2 5 12 15 8 14 16 10 13 6 2 9 3 5 11 1 7 4 4 7 16 6 8 2 5 14 10 1 11 13 3 9 15 12 14 12 15 8 10 13 6 16 9 3 5 2 4 11 1 7 6 4 7 16 2 5 14 8 1 11 13 10 12 3 9 15 3 5 2 9 7 4 11 1 8 14 12 15 13 6 16 10 11 13 10 1 15 12 3 9 16 6 4 7 5 14 8 2 15 8 14 12 6 16 10 13 5 2 9 3 1 7 4 11 7 16 6 4 14 8 2 5 13 10 1 11 9 15 12 3 2 9 3 5 11 1 7 4 12 15 8 14 16 10 13 6 10 1 11 13 3 9 15 12 4 7 16 6 8 2 5 14
from which it can be seen that the compound diffusion phase rearranges the bytes passing through it in the appropriate manner to meet the design goal of complete diffusion by means of the bit swap phases combined with the nonlinearity phases: each column contains all the numbers from 1 through 16. As should be apparent, when the table is doubled in height to reflect the two possibilities created by a bit swap phase, the potential sources added by the possibility of swapping are placed under the original sources.
Incidentally, in addition to the strength gained by using the bit swap and nonlinearity phases to provide additional diffusion, over and above the diffusion provided in the diffusion phases, since the nonlinearity phases use a fixed S-box rather than a key-dependent S-box, involving them more heavily in diffusion provides additional protection against weak keys in the cipher.
Immediately following the subkeys for the standard rounds, the 32-bit subkeys for the compound diffusion phases will be generated, and then S-boxes SR13 and SR14 will be generated. The long keys and exchange keys for the standard rounds with compound diffusion phases will be generated in the normal sequence based on the order in which rounds are performed.
For decipherment, the 32-bit keys for the compound diffusion phases must be reversed in groups of four, and the 16-bit halves of each key must be switched as well.
For Quadibloc 2002EA, the first group of standard rounds is now changed to consist of the following phases:
and the group of standard rounds in the middle of the cipher is changed to have the following structure:
and there is a group of six standard rounds at the end of the cipher having the precise reverse sequence of phases as that of the six standard rounds at the beginning of the cipher.
Thus, for Quadibloc 2002EA, the sequence of rounds becomes:
Six standard rounds Four core rounds Five standard rounds Four core rounds Six standard rounds
The subkey materials used by Quadibloc 2002EA become:
and the order in which the subkey material is produced becomes:
thus, the original EK13 through EK28 of Quadibloc 2002E become renumbered to EK19 through EK34 in Quadibloc 2002EA, and the original K193 through K496 of Quadibloc 2002E become renumbered to K265 through K568 in Quadibloc 2002EA.
Quadibloc 2002EA SR would have the number of rounds in it increased from 17 to 25, with the addition of eight rounds using compound diffusion phases.
In Quadibloc 2002EA W, each stage would continue to use exactly five standard rounds on the left half of the block, but their structure would become:
thus, with the removal of one greater diffusion phase using 32 subkeys, and the addition of two compound diffusion phases using 12 subkeys each, the total number of 32-bit subkeys used by the cipher would actually decrease; removing eight of them in each of four stages would reduce their number by 32. The total amount of subkey material used, however, would still increase, as two S-boxes, each having 256 entries each 32 bits long, would be added.
Quadibloc 2002EA ES is another case the key schedule for which should be treated explicitly, as it involves a significant modification to the use of the standard rounds.
The overall structure becomes:
Six standard rounds Eight new type rounds Six standard rounds Four core rounds Five standard rounds Four core rounds Six standard rounds Eight new type rounds Six standard rounds
and the order of key generation would become:
Again, things will be simpler with the availability of a concise table in which the key schedules for all the variants, when used with Quadibloc 2002EA, are given in summary form.
Quadibloc 2002EA
Variant:
-- SR DC W WS WD SD U WU RA RC RR ES RE RS RO WR
Bit Swap between 128-bit Halves of a 256-bit Block
64-bit subkeys, the bytes of which are produced by a 4-of-8 code
4 4 4 4 4 4
-- -- -- EK1 EK1 EK1 EK1 -- EK1 -- -- -- -- -- -- -- EK1
EK4 EK4 EK4 EK4 EK4 EK4
Greater Diffusion Phases within Standard Rounds
32-bit subkeys
192 298 192 384 384 384 384 192 256 192 192 192 320 320 320 192 256
K1 K1 K1 K1 K1 K1 K1 K1 K1 K1 K1 K1 K1 K1 K1 K1 K1
K192 K298 K192 K384 K384 K384 K384 K192 K256 K192 K192 K192 K320 K320 K320 K192 K256
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1 SB1
SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2 SB2
Standard Rounds (all)
128-bit subkeys
34 50 34 40 40 40 40 34 48 34 34 34 58 58 58 34 48
LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1 LK1
LK34 LK50 LK34 LK40 LK40 LK40 LK40 LK34 LK48 LK34 LK34 LK34 LK58 LK58 LK58 LK34 LK48
Lesser Diffusion Phases within Standard Rounds
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3 SB3
SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4 SB4
Standard Rounds (all)
64-bit subkeys, the bytes of which are produced by a 4-of-8 code
18 26 18 24 24 24 24 18 32 18 18 18 30 30 30 18 32
EK1 EK1 EK1 EK5 EK5 EK5 EK5 EK1 EK5 EK1 EK1 EK1 EK1 EK1 EK1 EK1 EK5
EK18 EK26 EK18 EK28 EK28 EK28 EK28 EK18 EK36 EK18 EK18 EK18 EK30 EK30 EK30 EK18 EK36
Compound Diffusion Phases within Standard Rounds
32-bit subkeys
72 96 72 96 96 96 96 72 96 72 72 72 120 120 120 72 96
K193 K299 K193 K385 K385 K385 K385 K193 K257 K193 K193 K193 K321 K321 K321 K193 K257
K264 K394 K264 K480 K480 K480 K480 K264 K352 K264 K264 K264 K440 K440 K440 K264 K352
S-boxes with 256 16-bit entries
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13 SR13
SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14 SR14
Encipherment of the Left Half of the Block within Core Rounds
32-bit subkeys
48 48 96 96 96 96 48 144 48 48 48 48 48 48 144
K265 -- K265 K481 K481 K481 K481 K265 K353 K265 K265 K265 K441 K441 K441 -- K353
K312 K312 K576 K576 K576 K576 K312 K496 K312 K312 K312 K488 K488 K488 K496
Left Half Encipherment: Preparing f-function Input
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
SB5 -- SB5 SB5 SB5 SB5 SB5 SB5 SB5 SB5 SB5 SB5 SB5 SB5 SB5 -- SB5
Core Round f-function
32-bit subkeys
256 256 512 512 256 256 256 256 256 256 256
K313 -- K313 K577 -- K577 -- K313 -- K313 K313 K313 K489 K489 K489 -- --
K568 K568 K1088 K1088 K568 K568 K568 K568 K744 K744 K744
Subkey Pools with 4 32-bit entries
512 512 768 768
-- -- -- -- SSP1 -- SSP1 -- SSP1 -- -- -- -- -- -- -- SSP1
SSP512 SSP512 SSP768 SSP768
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
6 2 6 6 2 2 6 6 6 6 6 6 6 6 6
SB6 -- SB6 SB6 SB6 SB6 SB6 SB6 SB6 SB6 SB6 SB6 SB6 SB6 SB6 -- SB6
SB11 SB7 SB11 SB11 SB7 SB7 SB11 SB11 SB11 SB11 SB11 SB11 SB11 SB11 SB11
Left Half Encipherment: Preparing f-function Input
64-bit subkeys, the bytes of which are produced by a 4-of-8 code
8 8 16 16 16 16 8 24 8 8 8 8 8 24
EK19 -- EK19 EK29 EK29 EK29 EK29 EK19 EK37 EK19 -- EK19 EK31 EK31 EK31 -- EK37
EK26 EK26 EK44 EK44 EK44 EK44 EK26 EK60 EK26 EK26 EK38 EK38 EK38 EK60
Core Round Combiner, Revised Versions
128-bit subkeys
16 16 16
-- -- -- -- -- -- -- -- -- -- LK35 LK35 -- -- LK59 -- --
LK50 LK50 LK74
32-bit subkeys
8 8
-- -- -- -- -- -- -- -- -- -- -- K737 -- -- K913 -- --
K744 K920
S-boxes with 256 16-bit entries
2 2
-- -- -- -- -- -- -- -- -- -- -- SR11 -- -- SR11 -- --
SR12 SR12
Core Round Combiner for Modifying the Right Half of the Block
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
SB12 -- SB12 SB12 SB12 SB12 SB12 SB12 SB12 SB12 SB12 SB12 SB12 SB12 SB12 -- SB12
SB15 SB15 SB15 SB15 SB15 SB15 SB15 SB15 SB15 SB15 SB15 SB15 SB15 SB15 SB15
Core Round Combiner: Accepting f-function Output
64-bit subkeys, the bytes of which are produced by a 4-of-8 code
8 8 16 16 16 16 8 24 8 8 8 8 8 8 24
EK27 -- EK27 EK45 EK45 EK45 EK45 EK27 EK61 EK21 EK21 EK21 EK39 EK29 EK29 -- EK61
EK34 EK34 EK60 EK60 EK60 EK60 EK34 EK84 EK28 EK28 EK28 EK46 EK36 EK36 EK84
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
SB16 -- SB16 SB16 SB16 SB16 SB16 SB16 SB16 SB16 SB16 SB16 SB16 SB16 SB16 -- SB16
Core Round f-function
S-boxes with 256 16-bit entries
2 2 2 2 2 2 2 2 2 2 2 2
SR1 -- -- SR1 SR1 -- -- SR1 SR1 SR1 SR1 SR1 SR1 SR1 SR1 -- SR1
SR2 SR2 SR2 SR2 SR2 SR2 SR2 SR2 SR2 SR2 SR2 SR2
New Type Rounds: Encipherment of First Quarter
32-bit subkeys
80 80 120 120 80 120 120 120 120
-- -- -- -- -- -- -- K569 K497 K569 -- K569 K745 K745 K745 K265 K497
K648 K576 K688 K688 K824 K864 K864 K384 K616
S-boxes with 256 16-bit entries
2 2 2 2 2 2 2 2 2
-- -- -- -- -- -- -- SR3 SR3 SR3 -- SR3 SR3 SR3 SR3 SR3 SR3
SR4 SR4 SR4 SR4 SR4 SR4 SR4 SR4 SR4
New Type Rounds: Preparation of f-function Input
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
1 1 1 1 1 1 1 1 1
-- -- -- -- -- -- -- SB17 SB17 SB17 -- SB17 SB17 SB17 SB17 SB17 SB17
New Type Rounds: f-function
32-bit subkeys
32 32 48 48 32 48 48 48 48
-- -- -- -- -- -- -- K649 K577 K689 -- K689 K825 K865 K865 K385 K617
K680 K608 K736 K736 K856 K912 K912 K432 K664
Subkey pools with 16 32-bit entries
128 256 192 192 128 192 192 192 384
-- -- -- -- -- -- -- SP1 SP1 SP1 -- SP1 SP1 SP1 SP1 SP1 SP1
SP128 SP256 SP192 SP192 SP128 SP192 SP192 SP128 SP128
New Type Rounds: f-function and combiner
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
5 5 5 5 5 5 5 5 5
-- -- -- -- -- -- -- SB18 SB18 SB18 -- SB18 SB18 SB18 SB18 SB18 SB18
SB22 SB22 SB22 SB22 SB22 SB22 SB22 SB22 SB22
New Type Rounds: f-function
S-boxes with 256 16-bit entries
4 4 4 4 4 4 4 4 4
-- -- -- -- -- -- -- SR5 SR5 SR5 -- SR5 SR5 SR5 SR5 SR5 SR5
SR8 SR8 SR8 SR8 SR8 SR8 SR8 SR8 SR8
New Type Round Combiner: Accepting f-function output (original and second alternate)
32-bit subkeys, the bytes of which are produced by a 4-of-8 code
16 32 16 16 16 16 16 16 32
-- -- -- -- -- -- -- SEK1 SEK1 SEK1 -- SEK1 SEK1 SEK1 SEK1 SEK1 SEK1
SEK16 SEK32 SEK16 SEK16 SEK16 SEK16 SEK16 SEK16 SEK32
New Type Round Combiner: Accepting f-function output (original)
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
1 1 1 1 1 1 1 1 1
-- -- -- -- -- -- -- SB23 SB23 SB23 -- SB23 SB23 SB23 SB23 SB23 SB23
New Type Round Combiner: Accepting f-function output (first alternate)
16-bit subkeys, the bytes of which are produced by a 4-of-8 code
8 8 8 8 8 16
-- -- -- -- -- -- -- -- -- TEK1 -- TEK1 -- TEK1 TEK1 TEK1 TEK1
TEK8 TEK8 TEK8 TEK8 TEK8 TEK8
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
3 3 3 3 3 3
-- -- -- -- -- -- -- -- -- SB24 -- SB24 -- SB24 SB24 SB24 SB24
SB26 SB26 SB26 SB26 SB26 SB26
S-boxes with 256 16-bit entries
2 2 2 2 2 2
-- -- -- -- -- -- -- -- -- SR9 -- SR9 -- SR9 SR9 SR9 SR9
SR10 SR10 SR10 SR10 SR10 SR10
New Type Round Combiner: Accepting f-function output (second alternate)
S-boxes with 256 8-bit entries, forming a permutation of the values 0-255
3 3 3 3 3 3
-- -- -- -- -- -- -- -- -- SB27 -- SB27 -- SB27 SB27 SB27 SB27
SB29 SB29 SB29 SB29 SB29 SB29
Appended Key Material For Symmetric New Type Round Swap Variants
Variant:
US WUS RAS RRS ESS RES RSS ROS WRS
32-bit subkeys
32 32 48 48 32 48 48 48 48
K681 K609 K737 K737 K857 K913 K913 K433 K665
K712 K640 K784 K784 K888 K960 K960 K480 K712
S-boxes with 256 16-bit entries
2 2 2 2 2 2 2 2 2
SR15 SR15 SR15 SR15 SR15 SR15 SR15 SR15 SR15
SR16 SR16 SR16 SR16 SR16 SR16 SR16 SR16 SR16
Next
Start of Section
Skip to Next Chapter
Skip to Next Section
Table of Contents
Main Page