Quadibloc 20 was designed to improve on ciphers such as Treyfer in order to obtain security against the slide attack, as well as against differential and linear cryptanalysis. As it used a 256-entry S-box whose contents were essentially random, it is likely to be secure against the XSL attack of Courtois and Pieprzyk as well, at least as they are currently conceived.
However, as this cipher was designed to be very minimal, it is quite likely that some attacks will be found that would be effective against it. In looking at the possibility of improving the cipher, I considered changing the f-function to one that was 16 bits wide instead of 8 bits wide, and noted the resemblance to SKIPJACK such a construction might have. However, if I was going to include a key-dependent S-box, making it bijective would introduce complication into the key schedule. Thus, I decided to use random S-boxes; this meant they needed to be at least 16 bits wide to reduce the probability of duplicate entries; thus, constructs from earlier ciphers in the Quadibloc series suggested themselves, and an f-function 32 bits wide was used.
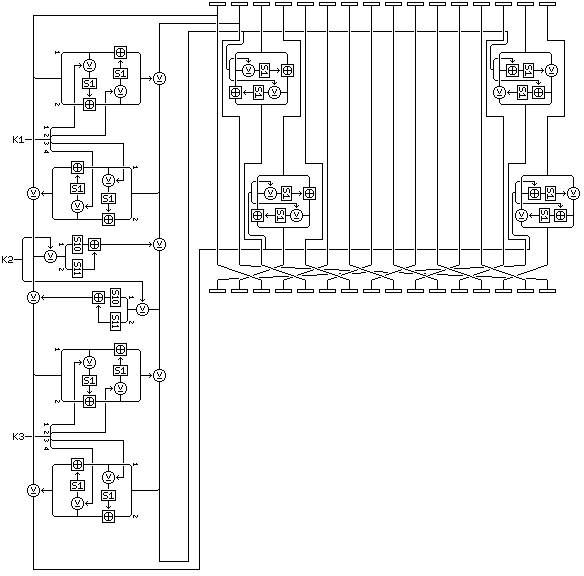
The round on which I finally settled was:

and this round operates as follows:
The first two 16-bit subblocks of the block are used as input to an f-function. This f-function consists of three pairs of Feistel rounds, each pair taking a 32-bit subkey as input. The first and third pairs use as their f-function a two-round Feistel structure; the second pair uses an f-function consisting of the XOR of half the subkey followed by using the two bytes of the result to index into key-dependent S-boxes S10 and S11, to find two values which are added using 16-bit binary addition. The leftmost byte of each entry is regarded as the most significant byte.
Except for the use of S-box S1 as generated from Euler's constant instead of S4, these operations are as found in Quadibloc 2002.
The first 16 bits of the f-function output are applied to the third and fifteenth 16-bit subblocks of the block; the second 16 bits of the f-function output are applied to the fourth and sixteenth 16-bit subblocks of the block. Note how the combiner is different in each case.
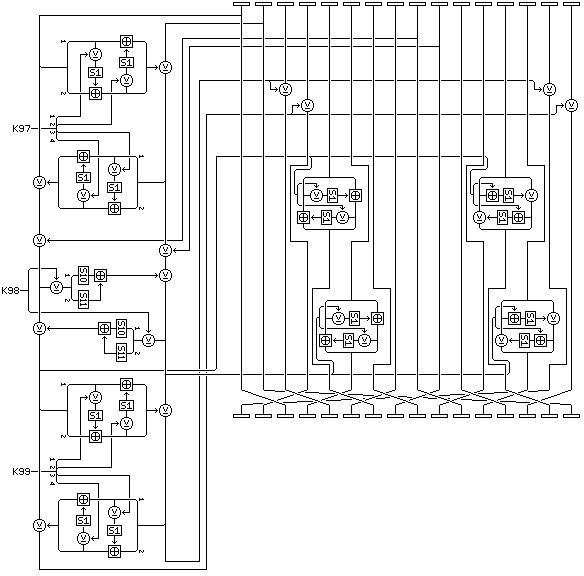
The bulk of the cipher, however, uses the following modified version of it, with only a few 16-bit XOR operations added, and considerably faster diffusion:
but the faster diffusion is obtained at the cost of possibly exposing intermediate results.
Here, the final results are simply XORed to the block, and the second intermediate value within the f-function is applied using the combiners from before, but with the fifth, sixth, thirteenth, and fourteenth 16-bit subblocks of the block. As well, the ninth and tenth 16-bit subblocks of the block are XORed with the first intermediate value within the f-function, to further hasten diffusion.
The cipher operates on a 256-bit block, considered as being divided into 16 subblocks of 16 bits each.
The rounds will be in groups of eight, which will be referred to as cycles. After the first seven rounds in each cycle, as shown in the diagram, the 16-bit subblocks of the block will be moved from the order:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
15 4 1 6 3 8 5 10 7 12 9 14 11 16 13 2
The cipher will consist of thirty-two cycles. After each cycle except the last, the 16-bit subblocks of the block will also be rearranged, but this time from the order:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
4 15 6 1 8 3 10 5 12 7 14 9 16 11 2 13
The first four cycles, and the last four cycles, will be composed of simple rounds, and the other twenty-four cycles, from cycle 5 to cycle 27, will be composed of the modified rounds that increase the pace of diffusion by using intermediate results.
The first round uses subkeys K1 through K3, the second subkeys K4 through K6; thirty-two cycles of eight rounds each make 256 rounds, so the cipher uses 768 32-bit subkeys from K1 through K768, in addition to two S-boxes containing 256 entries, each 16 bits in length.
The key shall be a multiple of 32 bits in length.
To simplify implementation, the cipher itself will be used to produce its own key schedule; a very simple key schedule produced directly from the key will be used for that process.
The 256-bit starting value:
55 33 0F AA CC F0 55 55 33 33 0F 0F AA AA CC CC F0 F0 0F 1E 2D 3C 4B 5A 69 78 87 96 A5 B4 C3 D2
will be repeatedly enciphered by cycles composed of modified rounds. The 256-bit value at the end of the first cycle will be used as K97 through K104, the 256-bit value at the end of the second cycle will be used as elements 0 through 15 of (an initial value, to be subsequently further modified, of) S-box S10, the 256-bit value at the end of the second cycle will be used as K105 through K112, and the alternation will continue until S-box S11 is filled. Thus, at the end of the sixty-third cycle, the 256-bit value will be used as K345 through K352, and at the end of the sixty-fourth cycle, the 256-bit result will be used as elements 240 through 255 of S-box S11.
Then another cycle of eight modified rounds will be performed, and the 256-bit result will be retained.
Then at the end of the 66th cycle, K353 through K360 will be taken, at the end of the 67th cycle, K361 through K368 will be taken, and so on until the 105th cycle produces K665 through K672.
Then, another cycle of eight modified rounds is performed, and the result has the previous retained value XORed with it.
Then the 107th cycle will be performed with eight regular rounds, and the 108th cycle will be performed with eight modified rounds. The result will be used as K1 through K8. Eleven additional pairs of cycles will produce K9 through K96, and then twelve additional pairs of cycles, one with regular rounds and one with modified rounds, will produce K673 through K768.
The key material used for the rounds that produce the key schedule will be produced from the key as follows: a copy of the key, followed by the inverse of its first byte, then a copy of the key followed by the inverse of its second byte, and so on; then, when it is time to return to the inverse of the first byte again, that inverse is incremented by one.
Initially, the entries of S10 and S11 will be filled as follows: the first byte of each element of S10 will be filled with the corresponding element of S1; thus, the N-th byte will be S1(N). The second byte will be S1(S1(N)), the third byte S1(S1(S1(N))), and this pattern will continue through the bytes of the elements of S11.
During subkey generation, the intermediate results of the first seven rounds in each cycle will be used to modify the contents of these temporary S10 and S11 boxes, by being XORed with them, starting with the first four elements of S10. Both boxes will have been modified once in their entirety at the end of the second round of the 19th cycle; each time this modification begins again with the first four elements of S10, the procedure will alternate between modifying groups of elements in consecutive order, and modifying groups of four elements in the area formed by the concatenation of S10 and S11 using a step size of thirty-six elements (thus skipping 32 elements between every 4 elements modified). This takes into account the fact that a single round does not modify all the elements of a 256-bit block.
Note that separate storage is required for the S10 and S11 used in key generation and the S10 and S11 it produces for use in the cipher.
At the conclusion of key generation, the temporary S10 and S11 are used to modify the actual S10 and S11 as follows: the entries of the temporary S-boxes are taken in pairs. The first item of the pair indicates, by its two bytes, an element of S10, and an element of S11, to be swapped. The second item of the pair is then XORed with the elements of S11 and S10 having the same positions as the elements of S10 and S11, respectively, that were swapped.
This last step should lead to the S10 and S11 used in the cipher having a structure which is not simple to analyze.
This cipher is designed to be very simple to code, although it will be slow to execute because of the large number of rounds.
Instead of being designed to be simply impossible to analyze in general terms, however, like Quadibloc 2002, or Quadibloc 2002EA U, its design incorporates many features aimed at specific known attacks. Thus, although stronger than Quadibloc 20, there definitely is the risk that a new attack might be found against Quadibloc 21.
The cipher is protected against differential and linear cryptanalysis by the large number of rounds, and the use of a key-dependent S-box.
The cipher is protected against slide attacks by the use of four cycles of simple rounds at the beginning and end of the cipher, by the use of a different re-ordering of subblocks at the end of each cycle, and by a key schedule that changes after S10 and S11 have been filled, as well as giving special treatment to the first and last four cycles.
The noninvertibility operation used before providing keys to the cycles composed of simple rounds is designed to prevent these rounds from providing clues to the rest of the subkeys. And the simple rounds protect the core rounds, which obtain faster diffusion, but take the risky step of using intermediate values from the f-function. Note, too, though, that the intermediate values are shielded by the final value from another round in the same cycle; given the inputs and outputs from a cycle, each subblock is modified four times, so one would need to somehow relate at least four sets of inputs and outputs to work backwards to the subkeys.
However, despite the use of different combiners, making the relation complicated, the key-dependent S-box is used only upstream of the portion that differs for the four places where f-function results are applied to the block, so that does leave open the possibility that some way to relate multiple cycle inputs and outputs can be found.
Although the S-boxes S10 and S11 are initially generated from equally-spaced outputs from repeated rounds of the cipher with a simple key schedule, again leaving open the possibility of some sort of algebraic structure connecting their contents, they are then moved around by a final scrambling step. But this step chooses 256 elements at random to move in each table; some will be duplicates, so, on average, about a quarter of the entries in each table will not be displaced. Also, while values are also XORed to the table, these values are XORed twice rather than once, and so, in addition to a similar portion of the entries being unaffected, even when an XOR takes place, some vestiges of the table's original structure will remain.
It does seem that these weaknesses are far too slight to admit of being exploited in any way. Avoiding them would have led to a return to a much more complex design. Possibly Quadibloc 21 complements, in its strengths and weaknesses, such ciphers as Quadibloc XIX, which have very complex key schedules and elaborate designs.
One weakness outlined above, that the use of only constant S-boxes in the parts of the f-function that are sometimes skipped allows the possibility of establishing algebraic relations linking the final output from the f-function and the intermediate result output, and as well the two inputs, can, however, be easily remedied by replacing the modified inner rounds of the cipher with the following further modified form:
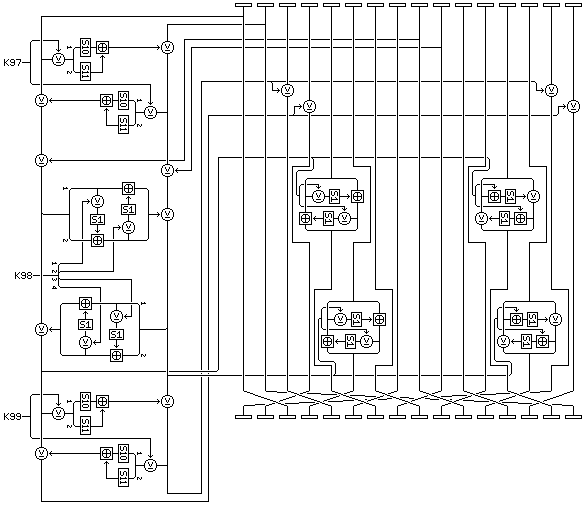
The resulting form of Quadibloc 21 can be referred to as Quadibloc 21 IR (Indeterminate Relation).
Note that, because of the possibility of bias in S-boxes S10 and S11, the equivalent modification is not made in the simple rounds, so that in those, at least, four Feistel rounds with the S-box S1 occur in the f-function.
Next
Start of Section
Skip to Next Chapter
Skip to Next Section
Table of Contents
Main Page