This cipher is based on the constructs used within Quadibloc 21. While Quadibloc 21 was designed to improve on Quadibloc 20 by further increasing resistance to known attacks, including the new XSL attack, Quadibloc 22 aims at obtaining resistance even to unknown attacks by being designed to be almost impossible to analyze. Thus, the series of ciphers from Quadibloc 20 to 22 shows a gradual increase in complexity, with Quadibloc 22 being an attempt to return to the levels of complexity and security found in most of the other Quadibloc ciphers.
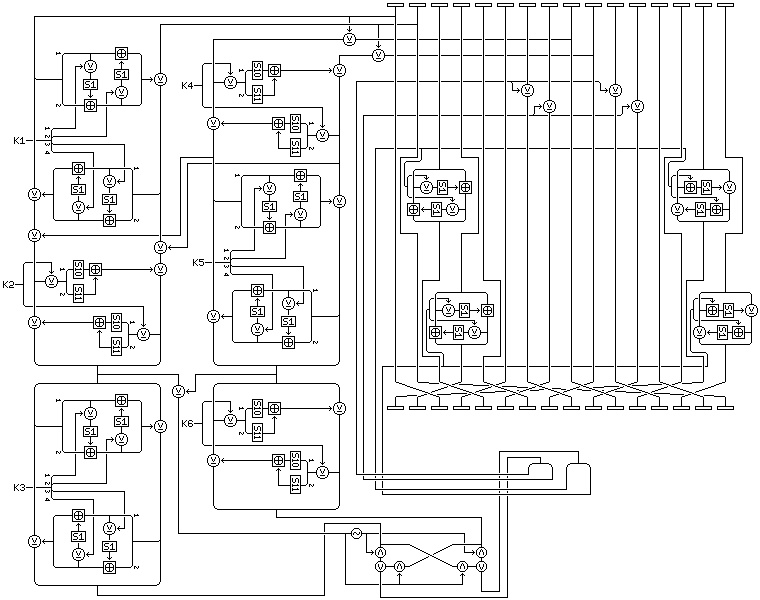
The basic Quadibloc 22 round is shown below:

Quadibloc 22 consists of only eight cycles of encipherment, with each cycle consisting of eight rounds. These cycles will be in pairs. The first, second, fifth, and sixth cycles will consist of rounds of the type shown above.
After the first seven rounds in the first, second, fifth and sixth cycles, as shown in the diagram, the 16-bit subblocks of the block will be moved from the order:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
15 4 1 6 3 8 5 10 7 12 9 14 11 16 13 2
After the first and fifth cycles, the 16-bit subblocks of the block will be moved from the order:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
4 15 6 1 8 3 10 5 12 7 14 9 16 11 2 13
as done between all cycles in Quadibloc 21.
The illustration below shows how the Quadibloc 21 round is modified for purposes of decipherment:
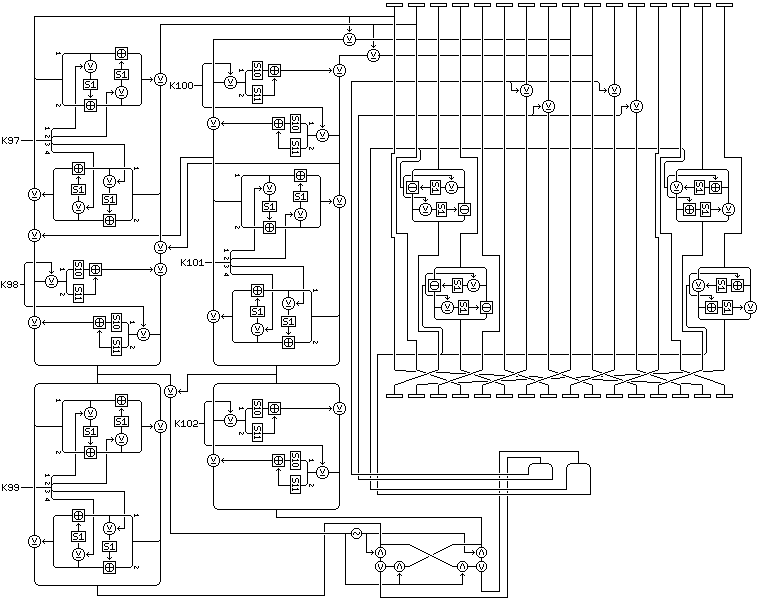
The round itself is only modified very slightly; only the combiners used to modify the third, fourth, fifteenth, and sixteenth 16-bit subblocks are changed. The reearrangement of blocks after the first seven rounds of a deciphering cycle is changed, however, to the inverse of that used in encipherment; thus in that case, the subblocks are moved from the order:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
3 16 5 2 7 4 9 6 11 8 13 10 15 12 1 14
and, at the end of a deciphering cycle which is followed by another deciphering cycle, the rearrangement becomes from the order:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
4 15 6 1 8 3 10 5 12 7 14 9 16 11 2 13
Quadibloc 22 is designed so that only a change in key schedule is required to decipher. Hence, deciphering rounds are used during encipherment as well; the third, fourth, seventh, and eighth cycles are composed of deciphering rounds. Thus, during those cycles, the rearrangement within deciphering rounds is used, and the rearrangement between deciphering cycles is used after the third and seventh cycles.
In order that the deciphering rounds do not invert the encipherment produced by the enciphering rounds, the rearrangement at the transition between enciphering and deciphering rounds consists of a transpose of the sixteen 16-bit subblocks, shifting them from the order:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16
and this is used after the second, fourth, and sixth cycles.
While twice as many subkeys are needed per round in this cipher, only one-quarter as many rounds are required by it as by Quadibloc 21, so Quadibloc 22 uses 384 subkeys, each 32 bits in length, from K1 through K384.
For decipherment, the order of the subkeys taken in groups of six is reversed, with the order of subkeys within each group of six remaining unaffected.
The key schedule will be very similar to that of Quadibloc 21.
Once again, to simplify implementation, the cipher itself will be used to produce its own key schedule; a very simple key schedule produced directly from the key will be used for that process.
The 256-bit starting value:
55 33 0F AA CC F0 55 55 33 33 0F 0F AA AA CC CC F0 F0 0F 1E 2D 3C 4B 5A 69 78 87 96 A5 B4 C3 D2
will be repeatedly enciphered by cycles composed of enciphering rounds. The 256-bit value at the end of the first cycle will be used as K1 through K8, the 256-bit value at the end of the second cycle will be used as elements 0 through 15 of S-box S10, the 256-bit value at the end of the second cycle will be used as K9 through K16, and the alternation will continue until S-box S11 is filled. Thus, at the end of the sixty-third cycle, the 256-bit value will be used as K249 through K256, and at the end of the sixty-fourth cycle, the 256-bit result will be used as elements 240 through 255 of S-box S11.
Note that after S-boxes S10 and S11 are filled by the steps above, they will be further modified. Also, this S10 and S11 will be stored separately from the S10 and S11 used during the rounds which are used to generate key material. This will be explained further below, after the setup of the keys used for the rounds generating key material is explained.
Following the sixty-fourth cycle, remaining cycle results are only used as subkeys, so the sixty-fifth cycle produces subkeys K257 through K264, the sixty-sixth cycle produces subkeys K265 through K272, and so on until the eightieth cycle produces subkeys K376 through K384.
The key material used for the rounds that produce the key schedule will be produced from the key as follows: a copy of the key, followed by the inverse of its first byte, followed by a copy of the key in which every byte is XORed with the counter value 1, then a copy of the key, followed by the inverse of its second byte, followed by a copy of the key in which every byte is XORed with the counter value 2, and so on; then, when it is time to return to the inverse of the first byte again, that inverse is incremented by one.
Thus, this key schedule essentially involves two counters, one which is incremented by one after each occurence of a copy of the key, a single byte, and a modified copy of the key, and one which is incremented after as many occurrences of this cycle as there are bytes in the key.
Initially, the entries of S10 and S11 will be filled as follows: the first byte of each element of S10 will be filled with the corresponding element of S1; thus, the N-th byte will be S1(N). The second byte will be S1(S1(N)), the third byte S1(S1(S1(N))), and this pattern will continue through the bytes of the elements of S11.
During subkey generation, the intermediate results of the first seven rounds in each cycle will be used to modify the contents of these temporary S10 and S11 boxes, by being XORed with them, starting with the first four elements of S10. Both boxes will have been modified once in their entirety at the end of the second round of the 19th cycle; each time this modification begins again with the first four elements of S10, the procedure will alternate between modifying groups of elements in consecutive order, and modifying groups of four elements in the area formed by the concatenation of S10 and S11 using a step size of thirty-six elements (thus skipping 32 elements between every 4 elements modified). This takes into account the fact that a single round does not modify all the elements of a 256-bit block.
Note that separate storage is required for the S10 and S11 used in key generation and the S10 and S11 it produces for use in the cipher.
At the conclusion of key generation, the temporary S10 and S11 are used to modify the actual S10 and S11 and the key schedule as follows: the entries of the temporary S-boxes are taken in pairs. The first item of the pair indicates, by its two bytes, an element of S10, and an element of S11, to be swapped. The second item of the pair is then XORed with the elements of S11 and S10 having the same positions as the elements of S10 and S11, respectively, that were swapped, and, in addition, the two bytes of the second item of the pair are used to indicate two subkeys in the range that extends from K1 through K128 and from K257 through K384 to swap, where the byte values represent subkeys in the following manner:
Byte value Subkey 0 K1 1 K2 2 K3 ... 126 K127 127 K128 128 K257 129 K258 130 K259 ... 254 K383 255 K384
This further scrambles the two weakest groups of subkeys; the ones generated earliest from the constant value, and the ones generated after successive single cycles, instead of pairs of cycles with a value taken for the S-boxes in between. Doing so heightens the resistance of the cipher to slide attacks, and the multiple use of internal S10 and S11 values for such very different purposes should not create a usable weakness.
Note also that the swaps of S10 and S11 values are between elements of two different 256-element arrays, and so always result in movement, while the swaps of subkeys take place within a single group of 256 subkeys, and thus no swap takes place if both bytes of the 16-bit value used to govern the swap are the same.
Next
Start of Section
Skip to Next Chapter
Skip to Next Section
Table of Contents
Main Page