If one hearkens back to the schemes of previous chapters, such as the Hagelin machine, or the Vernam two-tape system, and allows the use of more key than is needed to achieve a given level of security, one can use the constructs we have met in this chapter to achieve, I believe, a fairly high level of security.

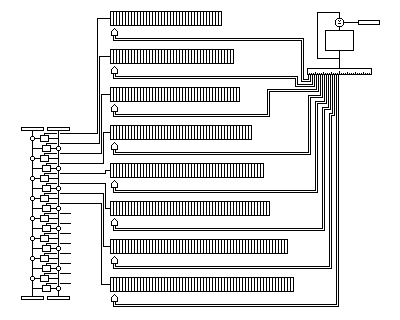
The diagram above is illustrative of the concept involved.
The diagram shows, however, a scaled-down version of the cipher. A more specific description rests on the following principle: the number of bits used to control the stepping of all the lists must equal or exceed the number of bits in a block. In this way, the stepping alone is enough, or at least nearly enough, to cause any plaintext block to become any possible ciphertext block, making it hard to obtain information about the subkeys in the lists. (In turn, the randomness and secrecy of the list contents make it hard to obtain information about the stepping sequence.)
A specific construction would run like this:
With a large key, key management is a problem. The key comes in four main parts:
The last item on the list is only needed as part of the key if one is going to start up the encipherment operation several times with the same lists of subkeys, but it is reasonable to do so, since that part of the key is very large and difficult to set up.
The first two items can be regarded as semi-permanent, while the last two should be changed with every message. However, the last two must be kept secret, not sent in the clear, otherwise attacks on the contents of the lists of subkey values can become possible if there is enough traffic for the same values of the first two items in the key.
With a key too large to send inside a public-key block, and such a high level of security as to be wasted by any practical method of key distribution, perhaps I have only solved the problem of cryptanalysis for the case when another solution to that problem already exists! However, one could use a one-time-pad to encipher the key distribution keys, and use this cipher with those keys for key distribution. That would avoid too great a loss of security.
The long-term portions of the key need to be couriered, of course, combined with encrypting them by some other, weaker, method. Sending two different couriers, by two different routes, with an XOR-split key may be appropriate here.
Although the design above already provides far more security than required for any practical purpose, against the kind of computing power that exists today, the possibility that a practical quantum computer might be constructed might be felt to be worthy of consideration. If the obstacles to constructing a quantum computer can be overcome, such a computer could essentially try all the possible keys to a block cipher at once, in a circuit the size of the conventional circuit used to apply a single key, and output the value of the key for the one case where some known plaintext is matched.
To protect against a threat like that, one would like a design that requires an inordinate amount of known plaintext before any facts about the key can be derived with certainty. A design like what we've just seen is perhaps a step towards that kind of cipher. This design can certainly be elaborated further, with yet another level of indirection, where a second block cipher produces the 64 bits that control the subkeys of the block cipher used to encipher plaintext. Further on, a diagram will show that type of design, but instead of the final block cipher enciphering plaintext, it will be used to encipher previous ciphertext to produce a 64-bit output used to encipher a single byte of plaintext.
Perhaps the second block cipher might be 32-round Blowfish, or even a modified Blowfish changed to use 48-bit subkeys and an expansion permutation along these lines:
23 32 9 18 1 2 3 4 5 6 7 8 31 8 17 26 9 10 11 12 13 14 15 16 7 16 25 2 17 18 19 20 21 22 23 24 15 24 1 10 25 26 27 28 29 30 31 32
so that the four S-boxes can each have 4,096 entries. To keep the time required to generate the S-boxes within some semblance of reason, though, I propose to use just 4-round Blowfish, rather than 32-round or 16-round Blowfish, for filling them.
Since I am going to extremes, instead of LUCIFER, let's let the 128-bit block cipher be the 40-round variation of Quadibloc II, using one of the more complicated variant round types. The stream cipher can consist of the XOR of the output of an expanded version of Gifford's cipher with the output of an elaborate MacLaren-Marsaglia construct.
Another preventive measure would be to use an enciphered random initialization vector that modifies the key in use for the next block of the message with message blocks that are always shorter than the size of the key, so that there is never enough known plaintext to attack any one key. Of course, the relationship between different message blocks and their initialization vectors can still be attacked; this device has been tried with simple ciphers and has not made them invincible. Applied to a sufficiently complex cipher, the gain in difficulty by using that trick, however, may, just possibly, be enough to provide some resistance to quantum computer attack.
This can be taken still further in the direction of wretched excess, in order to obtain increased security on the principle of an elephant giving birth to a gnat, by making use of the cipher-feedback principle of stream cipher design:
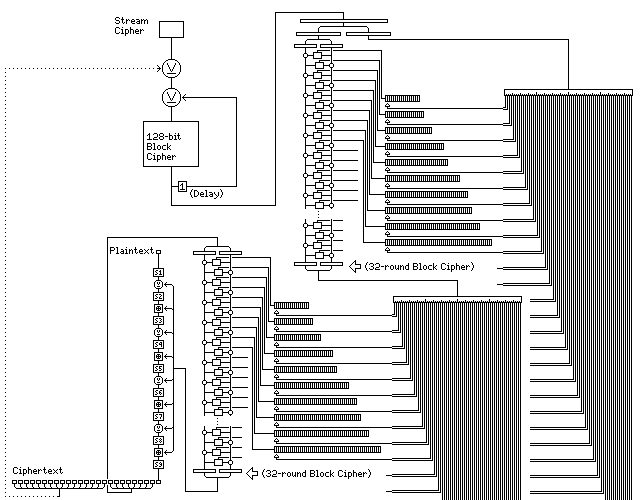
Here, we do not gain the advantages of limited error-propagation that a pure cipher-feedback design can offer; in fact, we not only have a large internal state, but previous ciphertext even influences that state, for the messy worst case of the autokey.
To encipher a single byte of the plaintext, we use the preceding twenty-four bytes of the ciphertext as input to the process. Sixteen bytes are XORed to the output of the initial stream cipher, which might as well be something elaborate, such as Panama or my modification of it; this is recirculated through a 128-bit block cipher.
Half of the result controls the subkeys for a 64-bit block cipher which enciphers the other half of the result.
The output of that cipher then controls the subkeys for another 64-bit block cipher which operates on the remaining eight bytes of preceding ciphertext.
And finally, that eight-byte output is applied to the one byte of plaintext being enciphered, being alternately added and XORed to it a byte at a time through eight layers of substitution.
Here we are: a truly secure symmetric-key cipher! And so it is, but it is outrageously excessive and wasteful. But perhaps the schematic diagram above will brighten a cubicle at the NSA and give some of the people there a chuckle.
Unless, of course, somebody actually implements this, and they would have liked to decrypt his traffic.
But, as noted, even the fact that this design is likely to produce (once the details are filled in) a genuinely secure cipher is not, in itself sufficient to mean it is suitable for practical use: a rough estimate of the time enciphering a message would take by this method is 64 times as long as it would take to encipher it with DES. Presumably, genuine security can be obtained at a somewhat lesser cost in computational resources.
Although wildly impractical in the specific form shown, before abandoning this design completely, some things should be noted:
An article in Cryptologia entitled The Aryabharata Cipher discussed the following idea for a cipher:
To encipher a message, generate a random series of letters as long as the message. Encipher the message with that series of letters by means of Vigenere.
Then, send the random series of letters in enciphered form, and also send the enciphered message, again enciphered as well.
Since both the pad and the message are sent, the absolute security of the one-time-pad is not obtained. But the pad and the message can each be enciphered in different ways, and because both are random, the cryptanalyst can only make progress by working on both together.
Perhaps doing so would be more difficult than cracking a simple double encryption, using the two ciphers applied to the two pieces of the message as expanded in sequence on the message instead. And perhaps not; it is hard for me to say for certain.
But it does seem as though forcing the cryptanalyst to relate different messages to crack a cipher creates a problem, although this happens anyways with modern ciphers of any difficulty. Thus, the scheme is of interest even if there is some question about whether this is the method referred to in the Indian classic.
Thus, I came up with the following scheme, which prevents progress from being made through attacking a single message in a different way, which also shows an alternate way of making effective use of a large key.
The following is a schematic diagram of how the scheme operates:
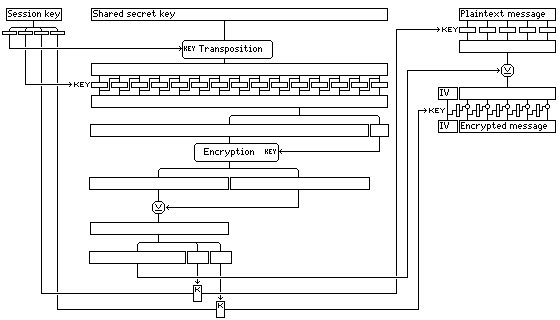
The steps involved in the encryption are described below:
The specific possibility for the additional encryption noted in the steps above is shown explicitly in this expanded version of the diagram:
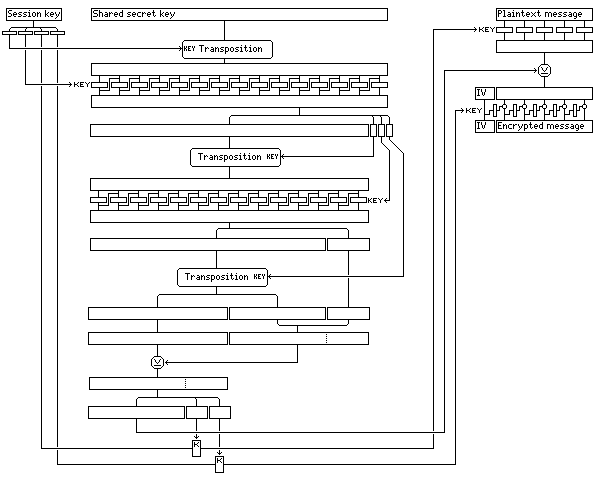
and although it is based on a different principle, the same concept that it is more difficult for a cryptanalyst to correlate multiple messages than to directly solve a single one is used as was used in the Aryabharata cipher. Of course, the possibility of still performing such correlations is exactly what allows modern ciphers to be attacked, through such things as differential cryptanalysis. As I propose using block ciphers currently considered secure in this, I hope it at least compounds the problem they create.
Note, too, that the message segment itself is encrypted first in ECB mode, to ensure that it goes through the block cipher, then by being XORed with bits that are a function of part of the session key and of the long secret key, then in CFB mode. So good error-propagation characteristics are still retained for the message segment.
In addition to error-propagation, the modes used mean that, since the encryption of the large shared secret key can be performed ahead of time, as long as a time lag between session keys and their use is present, and sufficient processing power is available, this method is not limited to off-line uses such as E-mail, but could be used on a continuous basis, even for a digital voice transmission or a similar application, since the plaintext need only be delayed by the simple operations directly performed on it.
Some additional discussion of ideas suggested by the "Aryabharata" cipher is on this page.
This cipher could be developed further. Instead of performing a transposition based on the session key first, before that, a simple stream cipher could be applied to the shared secret key. This way, a shared secret key with repeated bytes in it would not be weaker.
Also, a larger shared secret key could be used, so that the result of the encipherment operations performed on it could be used as input to a cipher like the large-key example which began this page.
If a one-time-pad is not available for transmitting session keys, perhaps something involving a large shared secret key could be worked out for that. With some further thought, it might be possible to develop a cipher that, while not posessing true information-theoretic security, might posess some degree of resistance even to attacks from quantum computers.
Next
Skip to Next Chapter
Chapter Start
Table of Contents
Main Page