The era of computers and electronics has meant an unprecedented freedom for cipher designers to use elaborate designs which would be far too prone to error if handled by pencil and paper, or far too expensive to implement in the form of an electromechanical cipher machine.
There are rumors that the secret cipher machines of the 1960s and beyond involved the use of shift registers, and, more specifically, that they used nonlinear shift registers, since it is known that a linear feedback shift register produces a sequence which, while it has a long period and an appearance of randomness, is not itself a secure additive key for a cipher. Since it is very difficult to guarantee that a shift register whose feedback is nonlinear will always have a reasonably long period, I think I will continue to doubt these rumors until the facts finally become declassified. (However, since the mathematical theory does exist by which the conditions for maximum period of the quadratic congruential generator are known, I definitely could be wrong.)
Well, I was wrong. Whether or not shift registers with nonlinear feedback were used in actual cipher machines, shift registers of that type with a guaranteed long period do exist. A recent paper by A. H. Chan, R. A. Games, and J. J. Rushaman, explained how a maximum-period binary linear-feedback shift register can be modified, by adding to it an additional "device" consisting of the XOR of a tap at one point to the AND of that tap and another tap as an additional term in the feedback function, with the resulting nonlinear-feedback shift register having the same period after the modification.
I can't provide a link to the paper, however - at the moment, I can't even find any indication online that it even exists!
However, some published papers use the term "nonlinear shift register" to describe a stream cipher system which has a linear feedback shift register at its heart, but which has as its output a nonlinear function of the shift register's state. Since it is trivially possible to produce any output sequence with the same period as the underlying LFSR in this way, (Proof: use the outputs from all the cells in the LFSR as inputs to the address lines of a one-bit wide ROM programmed, in a suitable order, with the desired sequence) I have no problem accepting the existence of nonlinear shift register designs in this sense.
Publicly known designs based on shift registers instead use linear shift registers, but do such things as combining the output from several, controlling the stepping of one shift register with another, as was done with the pinwheels in some of the more secure telecipher designs of the last chapter, or using one shift register to select between the outputs of two other shift registers.
But the main thrust of the computer era has been in the development of block ciphers, starting with the LUCIFER project at IBM, which was the direct ancestor of DES, the Data Encryption Standard.
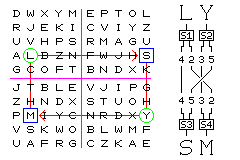
As a block cipher obtains its strength from operating on a large group of bits of fixed size, it belongs to the class of polygraphic ciphers, such as Playfair. The Four-Square cipher, being more uniform than Playfair, can be easily illustrated as a substitution-permutation network:

The most common case of Playfair, where the two letters are neither in the same row or column, would also have the same structure, but the other possible cases make it more complicated.
The substitution-permutation network was one of the basic concepts behind block ciphers, as it directly implemented Claude Shannon's concepts of confusion and diffusion.
Skip to Next Section
Table of Contents
Main Screen
Home Page