Some of the major integrity-aware modes discussed on the preceding page, IAPM and OCB modes, may be percieved as at least conceptually difficult to understand, even though they are still efficient. Couldn't a genuinely secure integrity-aware mode be based upon the type of relatively simple constructs found in the original basic encryption modes, or in PCBC, IGE, ABC, and DCTR modes? Actually, one existed, XECBS-XOR mode, described on the preceding page, of which I had been unaware when working on many of the modes described on this page.
This page contains several attempts on my part to achieve such a mode. My first attempt was occasioned by the publication of a paper which showed DCTR mode to be insecure.
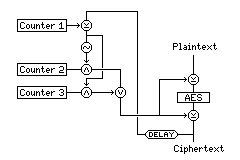
While the mode I then proposed, Triple Counter Cipher Feedback (TCCFB) mode, may still be of some interest, though, I now realize that it fails to fulfill the goals that DCTR mode was intended to achieve; unlike DCTR, it is not parallelizable. It still uses fewer block encryptions than IAPM, but if one is willing to perform multiplication, one can use CWC mode, which, unlike TCCFB, is proven to be secure if the underlying block cipher is secure.
This mode is illustrated below:

The name TCCFB is something of a misnomer, since the mode is probably more similar to Cipher Block Chaining than to Cipher Feedback mode, but I had chosen that name because it seemed to me that what I added to the original submitted mode, which was just called Dual Counter Mode, was similar to what was in CFB mode, while what resembled CBC mode had already been there.
Have three counters, all of which are (at least) double the block length in size.
Each counter is advanced by means of a mixed congruential PRNG.
The initial values of the counters, and their coefficients, are all secret. (Thus, in a system where keys for a message are derived from a public key method, they are included with the session key. Where public-key techniques are not used, or at least not used for every message, they are communicated with each message enciphered under a key-exchange key.)
The PRNG parameters must meet the conditions for maximal period. As well, the coefficient used multiplicatively is restricted to being in the range 01000...0001 to 10111...1101 to ensure a more varied sequence. (If, alternatively, a quadratic congruential generator is used, a similar condition, modified as appropriate to reflect the first condition, should be imposed on the coefficient used to multiply the quadratic term.)
A random IV, which need not be kept secret, is also sent with each message, and is treated as the block of ciphertext preceding the first one for purposes of carrying out the operations of the mode.
Encipherment of a block of plaintext proceeds as follows:
Of course, it might be claimed that this is much too complicated and elaborate to be called a mere cipher mode, but it seemed to me at the time that this is what it would take to be certain that weaknesses of the type found in DCM will not be a problem.
The entire value from each counter is completely changed from block to block, and the relationship between one value and the next is not known. As well, the use of previous plaintext creates a fundamental irregularity which makes it more difficult to find related blocks for purposes of mounting any kind of an attack.
Note, though, that the value XORed with the block before and after encryption is still definitely not cryptosecure, since by itself, it is vulnerable to a correlation attack, of the kind used against the Geffe generator, to get at the underlying linear sequences of the second and third counters. Although it is not cryptosecure, qualifying this as a cipher mode and not a new cipher in its own right, it should still be fully adequate when used in this mode with a block cipher in the middle.
However, performing three 256-bit multiplications per 128-bit block enciphered may be found unattractive. Can the counters safely be replaced by something simpler than truncated mixed congruential generators?
If the counters are not longer than the block, then at least the initial values for Counter 2 and Counter 3 must be chosen so that one is even and one is odd. But the result of that is that some of the bits of the value XORed with the plaintext and ciphertext vary in a regular way.
If one goes further, and uses a shift register in the fashion used for DCTR mode, obviously the retention of so many bits between encipherments at least seems dangerous. On the other hand, we can now get relatively prime periods by using shift registers of different lengths.
As a minimal precaution, though, the shift registers used for Counter 2 and Counter 3 should move in opposite directions. (Applying a bit transpose to Counter 1 before use, so that it effectively moves in a "third" direction, is attractive at least in hardware.)
Another way to drastically simplify the counters would be to make them counters; instead of a mixed congruential generator, just add an odd number to them each time, but at least have that odd number random and secret. Perhaps this could be mixed with shift register use; counter 1 could be of this type, while counters 2 and 3 were shift registers going in opposite directions. This would represent about the maximum possible simplification of this mode, and there is even the possibility that it would remain somewhat secure.
Or a mixed congruential generator could be used for counter 1 which was one byte wider than the block size, with a fixed multiplier of 100000001 (binary), to keep arithmetic very simple and yet retain some degree of unpredictability. The increment, as well as the initial value, would be variable and secret, and the increment would have to be odd. This, combined with two fixed maximum-period shift registers moving in opposite directions, might not be too bad. But there would still be strong correlations in the bits of the value generated to apply to plaintext and ciphertext, which could somehow be usable to a cryptanalyst seeking a way to interfere with message integrity.
Another simplification that might be tempting to some is not to simplify the counters, but to eliminate the use of the preceding block's ciphertext. This would make it possible to do encryption of multiple blocks in parallel. This might be safe, or it might suggest replacing the three counters by some rapid, but secure, keystream generator.
Of course, one could simply decide to be very elaborate, and go with something like the one shown in the following diagram, which I will call Quintuple Counter Cipher Block Chaining:
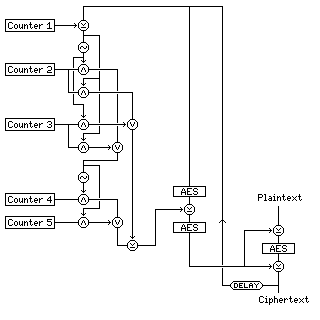
a triple-AES mode, using five counters, arranged in a construction I will discuss later in the section on hardware stream ciphers.
The first counter, XORed with the ciphertext of the previous block, is used to switch bits between the next two counters, to create two values, one used to select bits from either counter 4 or counter 5, the other used as a value to XOR with those selected bits.
Using five counters this way reduces vulnerability to correlation attacks.
The value so produced is XORed to the previous ciphertext between two additional AES encryptions.
Considerably later, I again turned my attention to constructing a simple encryption mode that would preserve message integrity, and my attempts to do so are chronicled below; my first attempt was based on Carl Campbell's Infinite Garble Extension mode, and I called it Offset IGE with Alternating Checksums (OIAC).
To encrypt a plaintext message P of length n blocks, the i-th block of which is denoted by P(i), proceed as follows:
Generate two random blocks of data, P(-1) and P(0), considered as being prepended to the message.
C(-1)=E(P(-1),k) and C(0)=E(P(0),k)
that is, these first two random blocks of data are enciphered using ECB mode encryption.
For all the blocks of the message proper, that is, for i=1 to n, and also for i=n+1 and i=n+2 as well, with the values for P(n+1) and P(n+2) to be defined later,
C(i)=P(i-1) XOR E(P(i) XOR C(i-2),k)
Thus, the encryption mode used for the main part of the message is the one illustrated below:
| | |
|---- |---- |----
| | | | | |
--> XOR | --> XOR | --> XOR |
| | | | | | | | |
| ----- | | ----- | | ----- |
| | AES | | | | AES | | | | AES | |
| ----- | | ----- | | ----- |
| | | | | | | | |
----> XOR ----> XOR ----> XOR -
| | | | | |
- | ----- | ----- | -----
|/ |/ |/
/| /| /|
------ |----------- |----------- |------
| | |
In addition, during encipherment of the message proper, that is, for i=1 to n, two 128-bit checksums, U and V, will be maintained. Initially, these checksums will have the following values:
U(0) = P(-1) V(0) = P(0)
When each block of the message is enciphered, again, for i=1 to n, these checksums are modified as follows:
U(i)=P(i) XOR V(i-1) V(i)=C(i) XOR U(i-1)
Note that the two checksums are swapped after the encipherment of each block.
Appended to the message, and enciphered in the same way as the body of the message, are two checksum blocks; these checksum blocks are the two checksums above, at the values they have after the message proper has been enciphered, as follows:
P(n+1)=V(n) P(n+2)=U(n)
The basic encipherment mode for each block of the message involves the plaintext of the immediately preceding block, and the ciphertext of the second block preceding, which is why the order given, and not the reverse order, is used.
The following diagram gives an overview of the encipherment of a complete message:
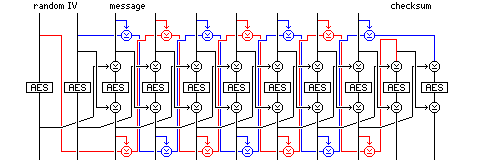
One may protest that the encryption mode involved is anything but simple. However, it involves no computation except one AES encryption for every message block, plus two extra ones at both the start and the finish of the message, plus a number of block-wide XOR operations. No Galois field arithmetic whatsoever is employed. And the checksum is twice the blocksize, the length required for equivalent security against collisions.
Any attempt to alter any part of the ciphertext of a message enciphered in this mode would affect both U and V, and it would affect one of them in a way that an attacker, not knowing the key for the block cipher, could not predict. And, in addition, U and V are both encrypted before being sent at the end of the message, and the encryption mode ties each one to the opposite chain of ciphertexts of the two ciphertext chains of odd and even ciphertexts each of which influences its successor through the message.
Is this mode secure? The first thing to note is that the checksums, U and V, are accumulated by simple XOR. Couldn't someone transpose the blocks of the cipher, and leave the checksums the same?
Because the encryption is not performed using ECB mode, the values of preceding blocks, in this case, the two blocks which precede any given block, affect encipherment. So if a ciphertext block is moved to a different location in the received message, it would decrypt to a different plaintext block, changing the checksum, despite the fact that it is nothing more than an accumulated XOR.
Unlike CBC, the plaintext, as well as the ciphertext, of earlier blocks affects encryption. So it isn't possible to XOR a bit vector with one ciphertext block, and make a controlled change to a following plaintext block, at the cost of garbling a block.
In thinking of how to make a simple encryption mode that could be proven, provided the block cipher used is secure, to provide message integrity, I noted that if one combines PCBC mode with a counter, as in the following diagram:
| CTR
| |
|------> XOR --->
| |
------- |
| AES | |
------- |
| |
|---------
|
then one obtains an output value that one can prove one can't duplicate by XORing the ciphertext value with any value, or by exchanging blocks between different points in the cipher; if the block cipher is secure, the only way for the XOR of the input and the output to bear any relationship to the XOR of a second input and output is if both the first and second inputs are identical, and if the counter is always changing, those identical values encountered in a different position in the cipher will produce a different final output from the construction shown above.
However, if one just uses PCBC mode with a counter, the fact that moving a block to a different position produces a different output can be balanced by XORing another value with the change caused by the change in position. Instead, to ensure that simply changing the value in any way causes a result that can't be cancelled out in a fashion that doesn't require one to have broken the block cipher used, one would have to apply it between two block encryptions. This seems to imply that one would need a double-AES mode, which would no longer provide the goal of integrity with single-pass encryption.
But CBC mode is a mode of encryption that can be thought of as providing multiple successive encryptions of data, although it does still allow the opportunity of cancelling out the results of changes of position, since the input and output of every block encryption is used directly: remove any number of blocks, and all one does is garble one block. The following construction attempts to eliminate any opportunity to change the positions of blocks:
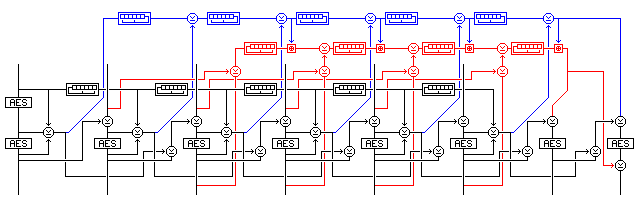
The encryption mode combines PCBC mode, CTR mode, and CBC mode as follows:
The input and output of the AES encryption of block i-2 are XORed together, and XORed with a counter.
The result of this is XORed to the ciphertext of block i-1.
The result of that XOR is then XORed to the plaintext of block i before it is subjected to AES encryption, which produces the ciphertext of block i.
The mode, as illustrated, involves two blocks of initialization vector, since blocks i-2 and i-1 are used in the encryption of block i. The first random block is encrypted an extra time, so that its original value can provide the initial value for the counter, which is a shift register.
Incidentally, when a shift register is used as the method of counter stepping, a measure needs to be taken to ensure the counter is not initially loaded with the all-zero value. One possibility is simply to use an initial counter value consisting of 127 bits of the first random value, with a 1 bit appended.
Two checksums are calculated by a simple CRC. One checksum is of the values formed from the XOR of the plaintext of block i-1 and the ciphertext of block i; the other is of the PCBC-CTR output values. These two checksums are calculated using shift registers moving in opposite directions, and they are then encrypted at the end of the message. Note that the PCBC-CTR output is summed using a shift register stepping in the opposite direction to that used for the counter, while the other checksum, isolated from the counter by two block cipher operations, goes in the same direction. To further prevent manipulations of the checksums, the first checksum also has the value of the second checksum added to it by modulo-2^128 addition. Also, this first checksum is XORed to the output value of the block cipher for the last block.
This mode is claimed to be immune from manipulation on the basis that if block i of the ciphertext is moved from another position, and it is attempted to XOR a value with block i+1 of the ciphertext (and hence block i+2 of the plaintext) to compensate for this move, one has irrevocably and uncontrollably changed the PCBC output value for the block cipher operation in block i+1.
With known plaintext, one has a set of block cipher inputs and outputs; with a secure block cipher, one cannot extend that set to other inputs and outputs. The requirement to compose a message in this mode, other than a message already encountered, would be to work backwards from the last block, using a known encryption for the last checksum block. Note also that it is still intended to keep the two IV blocks, in their original unencrypted form, locked within the encryption device. That, and the extra AES encryption of the first IV block, eliminates the one possible attack that seems to remain available: modifying a message by truncating its first few blocks, based on the fact that the relationship between successive counter values is known.
In my efforts to find an encryption mode that would provide integrity-awareness that I would also find satisfyingly simple, in the sense of avoiding advanced mathematics, allowing Galois field arithmetic in only grudgingly in the very limited form of making use of linear-feedback shift registers, I came up with a very complicated mode, of which a considerably simplified version is presented below:
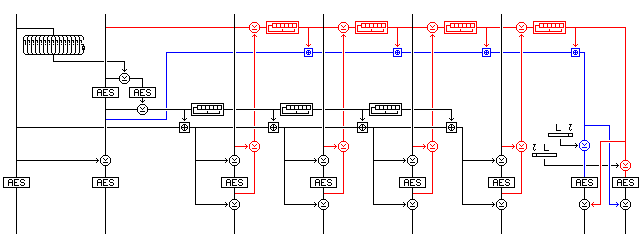
This illustration shows how Dual Checksum Counter-Whitening mode might work.
Incidentally, a detail addressed in the definitions of XECBS-XOR mode and CWC mode, among others, also applies to this mode. Encryption and decryption will work if ciphertext stealing is used for a last partial block, but if information about this is not somehow embedded in the integrity check, it would be the same as for a plaintext that is an integral number of blocks, of which the last block happens to partially match the ciphertext of the previous block in the appropriate way.
Because the counter is applied to the block both before and after encryption by an XOR, as in DCTR mode, and unlike what is done in XECBS-XOR, with sufficient known plaintext it is possible to detect collisions in the block cipher input and output with about 50% probability; if the XOR of a corresponding plaintext and ciphertext block are the same, this means the XOR of the block cipher input and output has that value as well, and, in a random codebook, when it does happen, it will usually happen only about once or twice. This is why a nonlinear counter with a 256-bit state is used, so that information about isolated counter outputs does not give information about the counter's complete state, and so that counter state collisions are rare enough to avoid birthday attacks.
Thus, although the mode employs the modulo-2^128 addition of XECB, it is actually more closely related to OCB mode in principle, if not in design decisions. This also suggests that additional security could be obtained by changing "XOR before and after" to "add before and XOR after" while retaining only one counter. That, however, does not work. It is true that one can no longer identify incidents where the input and output to the block cipher are the same by merely calculating the XOR of the plaintext and ciphertext. But if the difference between the inputs equals the XOR of the outputs, one has detected a likely coincidence.
If the value is applied to one side only, then coincidences can be detected by looking at the side not modified; with XECB, where the result is applied to the output by addition, one uses known plaintext. Two independent values are needed.
The scheme shown in the (anti-aliased by hand!) diagram below would just barely work,
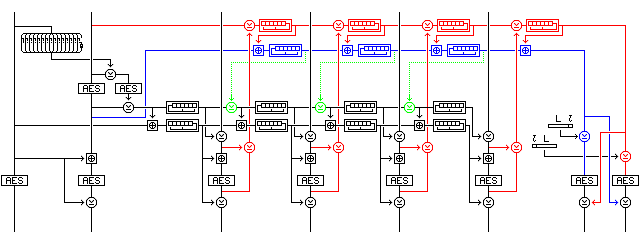
if the first XOR applied to the plaintext block before encryption were not present, because if one puts both a and b through a shift register, then a-b is not altered in a consistent way, and because a coincidence in the following block would be required to relate the two values used. Of course, adding considerably more complexity in the form of a second counter would be productive of an even greater degree of confidence.
It adds other complexity that is potentially useful; by performing shift register iterations on the accumulators, since these belong to GF(2) and are not closely related to the group formed by modulo 2^128 addition, the second-level checksum and the counter are now at least weakly cryptographic in nature themselves. If one uses the optional XOR indicated by the green portion of the drawing, the mode ceases to be parallelizable, and becomes strictly serial, but it would appear that an additional level of security is gained.
The extra block encryptions over XECB or OCB in this kind of mode may be put to use by using a different key for the IV and checksum portions of the mode; then, it may be that key extension can be obtained, as with DESX. Note, also, that if key extension of this sort can be obtained with this mode, then this mode would also have the useful property that, if the block cipher were used with a key of more than the block size (if AES, if AES-192 or AES-256 were used instead of AES-128), then the codebook attack, which involves collecting from known plaintext the entire 2^128 possible encipherments for a given key, would be barred, making the block cipher genuinely as strong as its key. Since a changing amount is applied to the inputs and outputs, differential attacks should also be made harder.
As for the shift registers in the diagram, starting from top to bottom, suggested values for them in the case of a 128-bit block cipher are:
The CRC checksum uses a shift register that moves to the right, and which is in Galois configuration, based on the polynomial:
128 120 112 104 96 88 80 x +x +x +x +x +x +x + 72 64 56 48 40 32 24 16 x +x +x +x +x +x +x +x + 12 9 7 5 2 x +x +x +x +x +1
thus, after the register is shifted one place to the right, XOR it with the hexadecimal constant:
A548 8080 8080 8080 8080 8080 8080 8080
if the bit shifted out is a 1.
The intent is to have one tap every eight bits, with the last few taps moved to create a primitive polynomial with no two adjacent taps; this is the principle used to find all the polynomials here, the next one after the goal which has no two adjacent taps is chosen.
The accumulating checksum of intermediate values of the CRC checksum uses a shift register that moves to the left, and which is in Galois configuration, based on the polynomial:
128 124 118 110 103 92 80 x +x +x +x +x +x +x + 74 66 61 51 45 38 31 21 x +x +x +x +x +x +x +x + 11 9 7 x +x +x +1
thus, after the register is shifted one place to the left, XOR it with the hexadecimal constant:
1040 4080 1001 0404 2008 3040 8020 0A81
if the bit shifted out is a 1. Here, there is also one tap every eight bits, but the positions of the taps are based on the octal expansion of pi.
The counter uses a shift register that moves to the left, and which is in Galois configuration, based on the polynomial:
128 126 124 122 108 106 x +x +x +x + ... +x +x + 103 101 99 97 75 73 x +x +x +x + ... +x +x + 70 68 64 62 18 16 x +x +x +x + ... +x +x + 12 8 4 2 x +x +x +x +1
with terms omitted whose exponents differ by 2; here, the first part of the polynomial has taps in alternating locations, except for two breaks where there are two spaces, instead of one, without a tap between taps.
The hexadecimal constant to be XORed with the register, if the bit shifted out is a 1, is:
5555 54AA AAAA AA55 5555 5555 5555 1115
Finally, the accumulator, to which counter values are added, uses a shift register that moves to the right, and which is in Galois configuration, and is based on the polynomial:
128 124 121 116 111 106 104 x +x +x +x +x +x +x + 101 99 96 92 89 84 79 75 73 x +x +x +x +x +x +x +x +x + 68 65 60 55 52 48 43 41 39 x +x +x +x +x +x +x +x +x + 34 32 29 24 20 x +x +x +x +x + 17 11 9 7 5 3 x +x +x +x +x +x +1
thus, when the regitster is shifted to the right, if the bit shifted out is a 1, the hexadecimal constant to XOR into the register is:
9550 4884 A150 8908 4851 0848 94A1 0848
Here, the number of spaces between adjacent taps in the polynomial is determined by adding one to the digits of the base-4 expansion of Euler's constant; this works down to the x^20 term, after which terms are shifted to find a primitive polynomial without adjacent taps. This primitive polynomial was a bit harder to find than the preceding ones, indidentally: all the others turned up in the first 32 primitive polynomials after the initial target, but this one was not even in the first 128 primitive polynomials generated.
To attempt to prove this mode is secure, provided the underlying block cipher is secure, one would need to proceed along the lines used in the proof of security for XECB.
If the underlying block cipher is secure, then the only block encryptions that can occur in the encipherment of a forgery are encryptions that have been seen previously in messages with known plaintext, unless it is not cared what either the input or the output of the encryption is. Since a forgery consists of a complete ciphertext, and the checksum involves every part of the plaintext, there can be no such "don't care" encryptions.
The forgery tactic involving taking an encryption involving ciphertext stealing, and expanding it to separate blocks (perhaps guessing at the bits that are enciphered twice, if there are few of them) or taking an encryption not involving ciphertext stealing, but with a last plaintext block that coincidentally matches the preceding ciphertext block in the right way as the basis for producing the message with ciphertext stealing, is forestalled by the use of the message length in the message digest.
A forgery involving chopping off the last few blocks of the plaintext requires a coincidentally appropriate set of block encryption examples to be available, because the checksum is not formed in the same way as blocks are encrypted (thus, a chosen plaintext with the last two blocks all-zero, for example, doesn't allow forgery of the message produced by encrypting all but the last two blocks, using the last two blocks of ciphertext as the checksum).
In the serial variation, it is true the checksum enters into the encryption of the blocks, but still in a way very different from the way in which it is used to produce the checksum. So neither the checksum, if a block is removed, zero or not, nor the block encryption of any block, has any way of resembling the checksum of a different message.
Note that the second block of the IV has the first block involved in its final encryption so as to prevent detecting either that its once-encrypted form is zero, or that it equals the first block, or that it equals the second block in any other message where the first block is not also equal. This makes detectable second-block coincidences as rare as both-block coincidences, provided a second-block coincidence is not somehow detectable from the way the message is encrypted.
Even if a proof of security following the lines of the XECB proof, as sketched above, were possible, it might only prove the presence of a lesser degree of security than is hoped for from this mode, which had the length of its IV and checksum chosen to maintain the full security of the underlying cipher. That is, until close to 2^128 blocks of known plaintext are available, the mode should hold its security, making it truly a "use-and-forget" mode, since no special limitations on its security would exist beyond those on the original cipher.
To show that the mode would benefit the security of AES-192 or AES-256 by preventing codebook attacks, or, if it won't, to find a mode that would, involves yet another order of difficulty, because now we would have to show that having known or chosen plaintext does not, in fact, enable one to compile a dictionary of block encryptions. The nonlinear nature of the counter and accumulator with its secret starting point makes it possible, but hardly certain, that this might be the case: the initial proof of security, for simplicity, assumes the opposite as a worst case.
This discussion may perhaps clarify the security goals I seek to achieve. I would like to develop a cipher mode that could be called a "perfect" cipher mode, one where any attack on the security or the integrity of messages is always as difficult as a brute-force search against the key. This is the security that is naïvely hoped for from encryption, since something in cipher seems to be a hopeless jumble to which nothing useful to an adversary could be done. Of course, the mode above would, even if it was fully successful in every way I might hope, due to the length of the integrity check and the IV, not achieve this if the block cipher has a key longer than 256 bits, or two blocks.
This design, though, is largely just a minor modification of XECSB-XOR, whose designers seem to have similar security goals. Can I come up with anything more original?
Here is a cipher mode that may be of some interest:
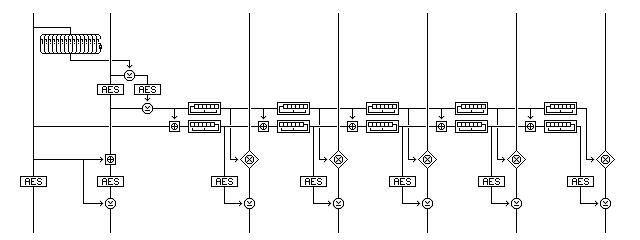
I was going to call this mode Galois Counter Mode (GCM), but that name has already been taken.
The proposed mode with a similar name is actually Galois/Counter Mode, or G/CM, but that is at least identical when spoken.
If the underlying block cipher is secure, then the message is clearly securely encrypted; it is XORed with a counter whose values have been enciphered using the block cipher. The use of a simpler earlier stage of the counter in the mode doesn't compromise this security, But what does it contribute?
The answer is complete immunity to bit-flipping attacks, as the multiplication shown is Galois Field multiplication over GF(2^128), which distributes over the exclusive-OR operation.
Given that the block cipher is secure, then any starting point value for the first level of the counter is as possible for any other for any message. Thus, the relationship between successive counter values is not useful for a bit-flipping attack. Or an existential forgery. Note that Galois Field multiplication of necessity involves whole blocks, and so this can't be treated like counter mode or output feedback mode; if the last block is incomplete, although it doesn't itself go through a block cipher operation, full ciphertext stealing must be performed.
Since the block cipher is secure, all we know about the outputs it produces from given inputs, if we do not know the key, is that if we give it the same input, we will get the same output, and if we give it different inputs, we will get different outputs. We will not know, from the output encrypted IV value, where in its fixed sequence the base counter starts. Will we be able to tell if, during the course of a single message, the second counter has a repeat, causing the encrypted value XORed with the blocks to be the same? Note also that enciphering the IV so that coincidences in the base counter aren't visible from the IV without a total coincidence is valuable here.
Even if this mode is theoretically perfect, if Galois Field multiplication requires 128 operations for every block, it may be less than practical. Specialized hardware might make such a multiplication as fast as regular multiplication, but that is no consolation for implementations on ordinary computers.
And, of course, 2^128 is hardly a prime number, which eliminates one possible alternative way of achieving full decorrelation.
No provision for a checksum is made; it is presumed that a simple XOR of the blocks in a message, encrypted as the last block, would serve as a checksum if the encryption mode were truly as perfect as intended.
I have since been informed that this mode, with such a checksum, is subject at least to existential forgery in the case of a known plaintext containing more than one all-zero block: so the encryption is not quite perfect.
Assuming one uses a simple modular polynomial, such as:
128 7 2 x +x +x +x+1
can we speed matters up?
The fact that the taps other than the first all fit in one byte allows a table with 256 16-bit entries to be used in reducing the raw product to one modulo the polynomial; this takes 16 steps. However, using four shifts and four XORs that are 136 bits wide, only one table lookup is needed. But the raw product still seems to require 128 shifts followed by a conditional XOR.
Still, this may perhaps be near the theoretical minimum required for any operation which must meet the goal that every bit of its result must depend on every bit of its inputs, or even one of those inputs. At least if one insists on operating on one of them one bit at a time. A multiplication table with 65,536 16-bit entries is an obvious optimization. One could even bring together two halves of the raw product in one operation, so that one avoids using 16-bit values at positions not aligned with 16-bit boundaries: and that optimization could make implementations doing a nybble-based multiplication practical as well: remain byte-aligned until one has to make just one shift of four bits at the end.
Of course, looking at the mode I have called Galois Counter Mode here suggests that the following mode, returning to the previous type of construction somewhat, would be secure:
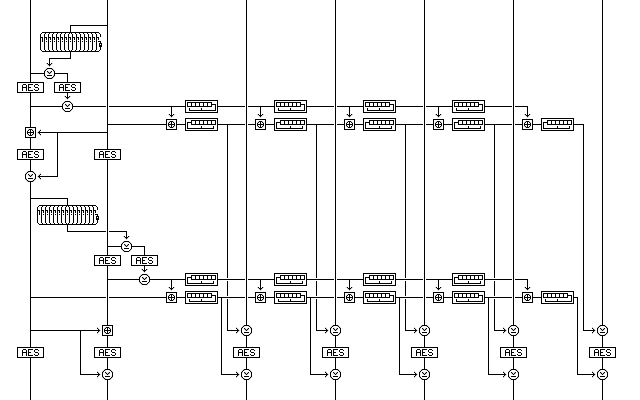
but with an overhead of eight additional block encryptions, even if secure it would seem to have little to commend it.
Of course, if one really wishes to get elaborate, for example, in the case of a block cipher with a 512-bit key, and if efficient algorithms are available for Galois Field multiplication and division by arbitrary values, there is always something like this:
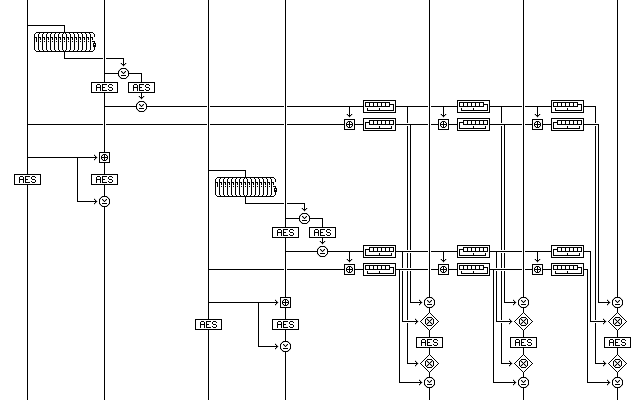
where we start with four random blocks. Addition modulo 2^128-1, with the out-of-range value 2^128-1 not altered, combined with a fast algorithm for the exponential and logarithm in the Galois field, or the operation of a * b xor b replacing a * b, would be other ways to provide full decorrelation.
Examining all these alternatives, upon reflection it seemed that a few minor changes to the Dual Checksum Counter-Whitening mode noted above would improve it:
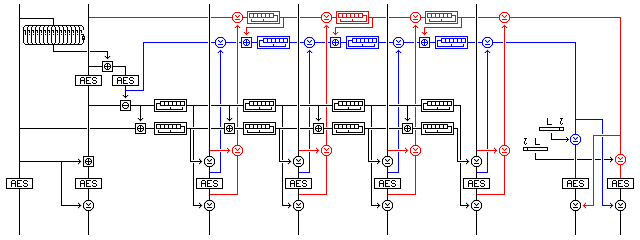
The process of enciphering a block is simplified. While 128-bit addition is still used at some points, it appears not to be necessary to follow XECBS-XOR in using it to apply a counter value in every encryption, since two different values are being applied to the block before and after encryption. A 128-bit addition is still done for every block, but only the one required to prevent the accumulating counter from being simple to analyze.
While a 128-bit addition is removed, an exclusive-OR is added to the checksum calculation, so that the accumulating checksum incorporates additional information about the message rather than simply incorporating additional information about intermediate values of the CRC checksum. The starting value for this checksum is also changed to make it more independent of the starting value of the other checksum.
Also, since the two checksums are going into an encryption that joins them, the last iteration of the interaction between them is not required. Note that the two-block encryption operation at the end has the weakness that if one block is the same in the input, that block in the output reflects the change in the bits of the other block. Because of the way the counters enter into the checksum, however, this weakness is not relevant to this mode; looking for collisions among 2^64 messages with an identical one-block chosen plaintext, for example, won't work as an attack.
While this mode is still related to OCB mode and XECBS-XOR mode, the relationship is no longer, therefore, as uncomfortably close as before, particularly in the latter case. Also, the four block encryptions used with the two-block IV are being employed almost as fully as possible to make the four starting values for the checksums and counters independent of one another; this independence is messy and imperfect in order to also guarantee that the starting value of the first counter is nonzero.
For each of the 2^128 possible starting values of the CRC checksum, there are only 2^120 possible starting values for the accumulating checksum, but, because the block cipher is secure, they are not related in a systematic fashion.
For each of the 2^128 possible starting values of the accumulating counter, the number of possible starting values for the shift register counter is not strictly determined, but should normally be of the order of 2^126. That number can never exceed 2^127, however, when an XOR is used to make the two block cipher inputs different, because each pair of inputs can occur in two orders. There are only 2^120 distinct distributions of these starting values, it must be admitted.
Two things remain the case, however: since the starting value for the CRC counter is produced based on an input of 248 random bits, nearly all the possible 2^128-1 values should occur, and for any one of those values, on average about 2^127 values, which will be, for all practical purposes, random, because the block cipher is secure, will be possible for the accumulating counter.
A nonce mode will also be defined. If instead of using a 256-bit random IV, it is desired to send a message number with each message that will be distinct for every message sent, then:
the message number may be up to fifteen octets (or 120 bits) in length,
and the counter and accumulator values used with the message shall be determined by the process for decrypting a message sent with the encrypted 256-bit random IV which consists of:
one octet containing the number of octets used to represent the message number, followed by
as many repetitions, with a possible partial repetition at the end, of the message number in most-significant octet first representation, as is required to fill the 256-bit area.
Note that the message number as repeated may contain leading zero octets, but it is permissible for an implementation to avoid leading zero octets and vary the number of octets used to represent the message number as well as using a fixed-length representation. While this avoids always having to test the message number for leading zero octets, it also means the encryption of a message depends on how the message number is, or is deemed to be, represented, and this does create a potential for confusion.
Perhaps always using the variable-length representation, and requiring implementations that do not wish to cope with testing leading octets for zero to begin assigning message numbers with the one having the value 1 in the most significant octet, thus losing 1/256th of the possible message numbers of a given length, is preferable, thus ensuring that every message number gives rise to a unique type of encryption for a given key.
The concern that leads to nonce versions of modes being defined is that many programs that use modes requiring a random IV do not generate a true random IV, but use a pseudo-random function to produce the IV, sometimes with a limited admixture of true randomness, for example, along the lines of ANSI X9.17.
However, while a nonce mode does provide security when real randomness is not available, attaching nonces to messages in this fashion may be felt to provide traffic analysis information in some cases. In a networked setting, where messages are encrypted at the time of transmission, using a timestamp as the nonce would add no information, but where messages are being encrypted by an application off-line, a message number would give information about other messages that, being sent at irregular intervals, might not have been intercepted. Thus, in addition to a nonce mode, a pseudorandom-IV mode, which could also be called a hidden-nonce mode, is also needed. This mode will require extra block encryptions; the mode of encryption itself is identical to encryption with a truly random IV, but the initial random value is replaced. I propose that it can be replaced by one produced by encrypting a 256-bit counter by means of the construction shown in the following diagram,
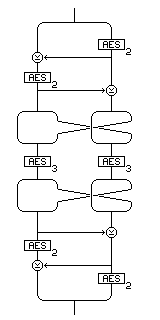
incorporating features from the Outerbridge construction and other methods of enlarged block encryption, using two other encryption keys. Messages in this mode do not need to be labelled to distinguish them from messages with real random IV values.
It is my belief that the attacks proposed against the DCTR mode were in part invalid because that mode was implicitly intended to be used in what is explicitly described in the XECB paper as the "stateful" mode of operation.
From two random blocks of data, an elaborate procedure is defined to produce four starting quantities for the mode, which involves four block encryptions. If, as may happen, one is encrypting data with the block cipher after using public-key methods to establish a key for the current message only, it may happen that we have surplus key material available, for example, if Diffie-Hellman key establishment is used.
For this case, where there is a large amount of key material unavoidably available, I propose that in addition to the session key, seven blocks of key material be put to use as follows:
Two blocks are taken as the two initial random values; they are subjected only to two block encryptions, not four, along with the nonzero function being applied to the first of them, in order to produce the guaranteed-nonzero starting value for the counter.
Three blocks are taken as the starting values for the accumulator, the CRC checksum, and the accumulating checksum; so these blocks are now independent of each other and the two blocks used to produce the counter start value.
An additional two blocks are used to XOR with the two-block integrity check at the end of the message.
If one is using RSA instead of Diffie-Hellman, one might wish to lengthen the message only by a minimal amount, and to generate only two blocks of random data, not seven. In that case, one can simply generate the two random blocks as are normally used, and use them to produce the four starting values used in the mode. The two random blocks can be sent with the message, and so again only two block encryptions, rather than four, are needed for the first two blocks of the message.
Also, if the fact that the nonzero function has only 2^120 possible output values, instead of the ideal 2^128-1 possible output values, is a concern, it is possible to increase this by modifying the nonzero function by making use of the same principle involved in the use of its value.
If the first fifteen octets of its input are all zero, then the negation of their XOR will be 255, and therefore not zero. Instead of using this value as the sixteenth octet of the nonzero function, the sixteenth octet of the input could be involved as well in this manner: take both the substitute of that sixteenth octet, and the substitute of the value produced by taking the one's complement of the XOR of all the other octets, and performing an exclusive-OR between them and the sixteenth octet, in a fixed S-box of some type, and XOR the two outputs together to produce the sixteenth octet of the result.
This result is guaranteed to be nonzero when the XOR of the first fifteen octets is nonzero, and guaranteed to be zero when that XOR is zero. When it is nonzero, its value also depends on the sixteenth octet, so the number of possible outputs of the nonzero function is increased from 2^120 to a value that can approach, but never exceed, 2^127, even for an ideal S-box.
The original and modified versions of the nonzero function are illustrated below:
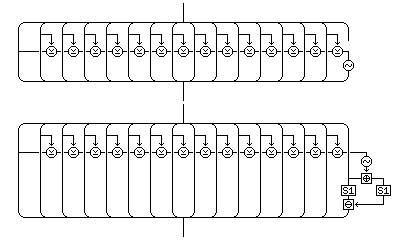
Incidentally, if XOR is used to differentiate the two S-box inputs, the S-box from Rijndael itself would be a very good S-box to use here, since its "flat XOR profile" is precisely the property desired to maximize the number of different possible outputs for any nonzero input from the other fifteen octets as the sixteenth octet varies through all of its possible values.
When addition is used, as shown in the diagram, the possible number of different possible outputs increases, but a different principle of S-box design is required; perhaps one that is much simpler? If the outputs are combined by subtraction instead of exclusive-OR, then indeed we have a classical problem. And if we were dealing with a prime number, instead of with 256, a circular slide rule would suggest the obvious solution. Could a table of Galois Field exponentials serve here, with XOR in the second position, then? Or would another approach work better, since the addition is modulo-256, not modulo-255?
If we try just a simple decimation, we get differences like this:
0 1 3 6 2 7 5 4 --------------- 1 3 6 2 7 5 4 0 1 2 3 4 5 6 7 4 3 6 2 7 5 4 0 1 3 5 7 1 3 5 3 5 6 2 7 5 4 0 1 3 6 1 4 7 2 1 4 7 2 7 5 4 0 1 3 6 2 6 2 6 6 2 6 2
which fall short of what we seek, which is to have every row like the first one, with exactly one duplicate.
If we subtract one from powers of 2, modulo 9, how well does that sequence behave? Unfortunately, 9 isn't a prime number.
0 1 3 7 6 4 2 5 --------------- 1 3 7 6 4 2 5 0 1 2 4 7 6 6 5 3 3 7 6 4 2 5 0 1 3 6 3 5 4 1 6 4 7 6 4 2 5 0 1 3 7 5 1 3 7 4 7 6
An interval method rotor wiring sequence isn't what is needed here either, even though it seems at least related:
2 1 0 3 7 6 5 4 --------------- 1 0 3 7 6 5 4 2 7 7 3 4 7 7 7 6
And then there's always Gray code; but that, with a difference of one, and an XOR output, would only give the single bit combinations, so it would be almost the opposite of what is sought.
Using a computer program to search through all the permutations of the numbers from 0 through 7 turned up no sequence with an ideal score of 7, but the first sequence with a score of 6, indicating at worst two duplicates, and one omitted difference, in any row, that turned up was this one:
0 1 3 2 7 5 6 4 --------------- 1 3 2 7 5 6 4 0 1 2 7 5 5 1 6 4 3 2 7 5 6 4 0 1 3 1 4 3 7 7 6 5 2 7 5 6 4 0 1 3 2 6 2 4 5 3 3 7 7 5 6 4 0 1 3 2 7 4 3 2 1 3 5 6 5 6 4 0 1 3 2 7 5 5 1 6 2 6 4 3 6 4 0 1 3 2 7 5 6 3 5 7 4 5 1 1 4 0 1 3 2 7 5 6 4 7 6 1 3 2 7 2
so using subtraction instead of XOR in the second step does not appear to make it a neat and tidy problem.
Still, if one squints enough, one might be able to make oneself imagine that one sees a sort of pattern. Perhaps the next step would be the sequence:
0 1 3 2 7 5 6 4 15 11 13 9 14 10 12 8
How well would this sequence behave when slid against itself?
0 1 3 2 7 5 6 4 15 11 13 9 14 10 12 8 ----------------------------------------------- 1 3 2 7 5 6 4 15 11 13 9 14 10 12 8 0 1 2 15 5 14 1 14 11 13 2 12 5 12 2 12 8
That seems obviously not to be the right extension.
Trying the other orders from 5 to 7 gives the following sequences, all of which have a score of one less than the ideal:
0 1 2 4 3 0 1 2 4 5 3 0 1 2 4 6 5 3
If one uses XOR instead of taking the difference between the two outputs, for order 8, the best score shrinks to 4 from 6, and it appears that even for a random S-box instead of one designed to maximize the score, subtraction is better for this purpose.
The following table, for order 8, of the scores for the 7! distinct cases, bears this out:
score Subtraction XOR 1 376 6,904 2 3,072 11,520 3 6,912 12,288 4 20,224 9,216 5 9,216 0 6 512 0 7 0 0
In any case, this mode really cannot claim to be any simpler than CWC or XECB. Is there such a thing as a simple mode that is integrity-aware, as it seems there should be?
What about combining Cipher-Feedback mode with a counter?
This wouldn't be parallelizable, of course. And it has, in fact, been suggested.
In any event, it seems that integrity-aware encryption is difficult. However, conceptually simple modes of integrity-aware encryption exist. For example, this kind of mode would work just nicely:
counter plaintext
| |
----- -----
|AES| |AES|
----- -----
| |
-------> XOR
|
-----
|AES|
-----
|
ciphertext
but it requires three block encryptions for every message block.
The complexity of integrity-aware encryption modes, therefore, is really caused by not being able, at least when one is using a hardware implementation of a block cipher, to apply a counter value to the block being encrypted after, say, half the rounds have been performed.
Next
Chapter Start
Skip to Next Chapter
Table of Contents
Main Page