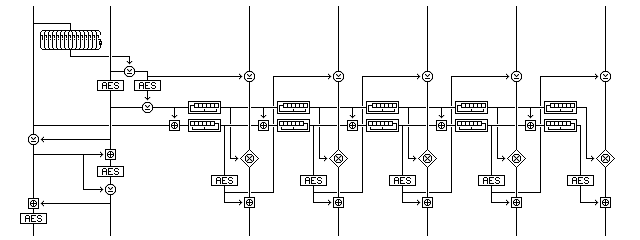
The following diagram illustrates an encryption mode that grew out of a failed attempt at a simple encryption mode that does not include any integrity checking in its definition, but which is intended to provide a nearly perfect "wrapper" around the plaintext, allowing almost any form of checksum to serve as an integrity check.

The mode operates as follows:
Two random blocks, R and S, are generated; their raw values are not disclosed to any untrusted parties, but are kept internally in any encryption device implementing this mode as if they were key material.
A block cipher, E(p,k), is used, with four encryptions of overhead, and one encryption for block of plaintext. Ciphertext stealing can be used for a short block at the end of a message, since the operations applied to each block depend only on the key and the counter state.
A value that is guaranteed to be nonzero is produced from the two random blocks as the initial value of the first counter, A, as follows:
The XOR of the first fifteen bytes of R is calculated, and a sixteen byte value consisting of those first fifteen bytes followed by the binary one's complement of that XOR is therefore nonzero, and is called N.
A is calculated as the result of E(S,k) XOR E(S XOR N,k); since N is nonzero, and E(x,k) is bijective, A cannot be zero.
The block pair (R, E(S,k)) is subjected to further encryption before being transmitted as the initialization vector for this encryption mode.
The first block is changed by having the current value of the second block XORed with it.
The second block has the first block added to it, modulo 2^128.
The second block is encrypted in the block cipher with the encryption key in use.
The second block is changed by having the current value of the first block XORed with it.
The first block has the second block added to it, modulo 2^128.
The first block is encrypted in the block cipher with the encryption key in use.
The first random block, R, is used as the initial value of the second counter, B.
The counters are advanced as follows before the encryption of each block:
The second counter, B, has the current value of the first counter, A, added to it by modulo 2^128 addition.
The first counter, A, is modified by being shifted one place to the left, and if the first bit shifted out is a one, it is XORed with the constant:
1040 4080 1001 0404 2008 3040 8020 0A81
thus, it is stepped through one of the Galois-configuration shift registers used in the mode described on the previous page.
The second counter, B, is modified by being shifted one place to the right, and if the last bit shifted out is a one, it is XORed with the constant:
9550 4884 A150 8908 4851 0848 94A1 0848
thus, it is also stepped through one of the Galois-configuration shift registers used in the mode described on the previous page.
A plaintext block is encrypted to produce a ciphertext block as follows:
It is XORed with the encrypted version of the previous value of the second counter;
It is subjected to a multiplicative operation with the current value of the first counter (which is never zero);
It has the encrypted version of the current value of the second counter added to it using modulo 2^128 addition.
In the case of the first block, there is no previous value of the second counter, so in the first step, the value XORed to the plaintext block is instead S xor N, which is also a value suitably protected by encryption.
What is the multiplicative operation? It must be an operation that provides decorrelation with either the preceding XOR or the following modular addition.
Since 2^128 + 1 is not a prime number, one prime candidate for the multiplicative operation, multiplying the input plus one by the current value of the first counter modulo 2^128 + 1 and then subtracting one from the result is eliminated, because it will not always be invertible.
An ideal multiplicative operation, Galois field multiplication, is certainly possible; this would decorrelate with the preceding XOR operation. But this is not a standard operation in computer arithmetic units, and so it might be unnecessarily slow.
Another possibility would be to use multiplication modulo a prime number below 2^128 for most values. Simply making no change to the block for the few cases where either the plaintext or the counter exceeded the limit would seem to pose little risk. The largest prime number below 2^128 is apparently:
340,282,366,920,938,463,463,374,607,431,768,211,297
which is 2^128 - 159.
Since addition with carries across subblocks resembles addition without such carries, another option is simply to split the block and the counter into 16-bit portions, and use multiplication modulo 2^16 + 1, which is prime, in each portion. Add one to the 16-bit counter segment, as well as to the input, and the fact that not every 16-bit subblock is not guaranteed to be nonzero is not a problem; the trouble taken to provide nonzero 128-bit counter values is only relevant to the case where Galois field multiplication is used as the multiplicative operation.
While this would still block bit-flipping quite effectively, there would now be a one-in-65,536 probability that some minor changes in either the plaintext or the ciphertext that leave one of the two checksums in the integrity-aware mode below unchanged would also leave the other checksum unchanged, thus using such a multiplicative operation would seriously limit the security of the mode against existential forgeries.
It may also be possible to make use of the fact that 2^127 - 1 is a Mersenne prime, leaving only one bit out in the cold, or that while the Fermat number 2^128 + 1 is not a prime, it does have only two factors, being
59,649,589,127,497,217
times 5,704,689,200,685,129,054,721
as discovered in 1975 by Morrison and Brillhart.
This is a mode that provides secrecy only. The intent of the multiplicative operation, that decorrelates with either the addition or the XOR operations used, is to provide certain other desirable security properties, so that adding integrity awareness will not be too difficult.
However, to achieve true integrity awareness, a degree of care, and some modifications to the mode, are still required. An integrity-aware mode based on the mode above can, I believe, be provided like this:
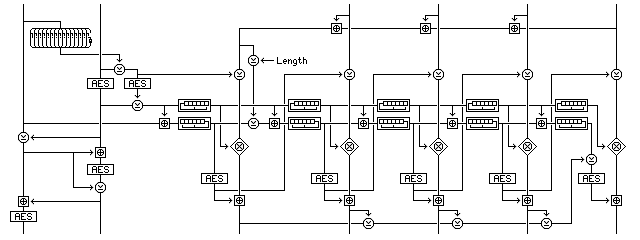
Here, ciphertext stealing may not be possible in a simple fashion; there may be a safe way to do it, but I have not attempted to determine the precise procedure for it at this time.
At first, looking at the diagram, one may find it impossible to credit the claim that this mode is integrity-aware. I begin by simply appending to the beginning of the message a modulo 2^128 sum of all the plaintext blocks of the message. I end by using a simple XOR checksum of all the ciphertext blocks of the message except the last. Since both of these checksums are left unaltered by rearranging blocks, or by many other manipulations, how can existential forgeries possibly be prevented?
For one thing, the blocks are not encrypted by a simple XOR. Thus, switching two plaintext blocks, or adding something to one plaintext block and subtracting it from another plaintext block, does not have the result of switching two ciphertext blocks, or XORing something to two ciphertext blocks. The multiplicative operation makes it particularly difficult to leave both checksums unchanged by a manipulation.
The relationship between successive values of the first counter is known, but its intial value is not, being kept behind a layer of encryption. Thus, even the relationship between succeeding values of the second counter is not known, and it is only used after being encrypted. It is, though, the weaker of the two counters that goes into the multiplicative operation.
For another thing, the first checksum, after having the message length XORed to it, is XORed into the second counter, modifying it, and the values of the second counter are encrypted when used, and the second checksum is XORed with the final second counter value before it is encrypted. Since both checksums end up being reflected in the final message in an encrypted form, provided the block cipher is secure, attempts to produce even an existential forgery by changing either checksum in a known way are not possible, only attacks involving simultaneously preserving both checksums can be made.
It may be noted that, except for the fact that 128-bit wide Galois Field multiplication, the ideal multiplicative operation for this mode, may be impractical, making it of theoretical interest only, and that the AES encryption of the counter value for the last block is not parallelizable, being dependent on the previous checksum, this mode has the same desirable properties as CWC mode. Unlike my previous attempt at an integrity-aware mode, it seems as though this mode is not entirely a thinly-disguised version of that mode, but actually contains some small glimmering of originality.
As noted above, there is one difficulty with these modes. Galois Field multiplication is not a standard operation for which microprocessor arithmetic-logic units are wired. Regular multiplication has the distributive property needed for decorrelation, but it does not seem to be available for this mode when used with block ciphers of appreciable size, because 2^128 + 1 is not a prime number.
However, there is a way around this, as the diagram below illustrates:

This performs the multiplications in a fashion reminiscent of a block cipher having rounds of the Feistel type, so that they do not need to be invertible for the same reason that the f-function of a Feistel round need not be invertible.
The three rounds involved allow each of two blocks to be decorrelated with its own multiplying factor. The last two rounds illustrate the basic principle clearly for the factor applied to the second block; if the second block is changed by one, then first the preceding block is changed by one when the value of the second block is added to it, and then the following block is changed by the multiplying factor when the first block, subjected to the multiplicative operation, is added to it.
The first round, however, seems to be operating differently. But that is because it takes the subsequent rounds into account. A change in the first block by one becomes a change in the second block by the multiplying factor. The second round then propagates that change to the first block. These similar changes don't tend to cancel out, however, because the third round propagates the change in the first block back to the second block. The fact that the multiplying factor is never zero ensures that the net multiple of the change in the first block may be three, but it is never two, a value more dangerous than zero since the ciphertext checksum is produced by an XOR rather than an addition.
If the total number of blocks involved is odd, the last block is then decorrelated with the involvement of the preceding block instead of the following block, so that single blocks, rather than block pairs, remain the fundamental unit of the encryption mode.
Similarly, again because the counter values are needed for decryption, the plaintext checksum with the length indication XORed to it can only be applied to the accumulating counter after it has already been used for the encryption of the first two blocks. As ciphertext stealing is defined for this mode, the length indication will consist of a 121-bit number of whole blocks in the message, followed by a seven-bit number from 0 to 127 of the number of bits in the final partial block; this number will be 0 if no partial block is present.
Also, because of the way in which the decorrelation now works, ciphertext stealing, which should be possible without compromising the integrity-checking properties of the cipher, has to be done in a somewhat unusual manner. If the final plaintext block is short, it can be padded by taking ciphertext not from the ciphertext block corresponding to the preceding plaintext block, but from the ciphertext block preceding that, in order that the final two ciphertext blocks remain untouched, permitting the value of the last plaintext block to be determined, which then releases the stolen ciphertext to allow the remaining portion of the message to be decrypted.
In addition, the stolen ciphertext cannot be included in the initial additive checksum of the plaintext, since that enters into the computation of the counter used for encipherment from the outset. In this case, the last, partial plaintext block must be considered to be padded on the right with zeroes for purposes of computing the additive checksum.
As well, since the decipherment of the last block, containing the stolen ciphertext, requires accurate knowledge of the ciphertext checksum, the stolen ciphertext must be excluded from the ciphertext checksum. Note also that, in order to permit the initial counter values to be recovered prior to attempting to recover the stolen ciphertext, the message length illustrated in the diagram, three full blocks plus one partial block, is the minimum permissible length for a message containing a partial block.
As the necessary procedure for ciphertext stealing for this mode is somewhat involved, it is illustrated in the diagram as well.
Let us make the multiplications in the diagram multiplications modulo 2^128, for the maximum in speed and efficiency. And let us say that someone were able to create an existential forgery. If so, what would that prove?
Given that the block cipher in use has a 128-bit block size, we will assume it has a 128-bit key, and is thus vulnerable to a brute-force search of order 2^128. Can an existential forgery be obtained more quickly against this mode?
We begin by noting that this mode is initialized using two random blocks, each 128 bits long. Thus, a birthday attack aimed at finding two messages with both random blocks identical would require 2^128 messages to be sent. The assumption is that the sum total of all legitimate message traffic could never generate that many messages, because 2^128 block encryptions are impossible to achieve.
Therefore, we can eliminate from consideration attacks based on having such a coincidence available.
What if just one of the two blocks matches? This is not detectable from the initialization vector, since only a function of both blocks goes into the two AES encryptions.
Also, if only one block, or the first block or the initial first counter value, matches between two messages, this does not prevent the sequence of values going into AES encryptions before being XORed and added to the blocks from being completely changed.
The sum of the plaintext blocks goes appears in the message as a modification of the second, accumulating, counter, whose values go through an AES encryption before use. The XOR of the ciphertext blocks goes through an AES encryption before modifying the final block. Thus, if the block cipher is secure, neither of these values can be altered. This mode doesn't yield any obvious plaintext-ciphertext pairs to substitute anywhere.
But it has an obvious weakness: the checksums allow rearrangements and reciprocal modifications of their inputs to take place.
Exploiting this "weakness" is what the decorrelation layer makes impossible. Because a weak counter is used as the input to the multiplicative operation, it is guaranteed that over the entire message, provided the message is shorter than 2^128 - 1 blocks, the multiplier never takes the same value twice. Because a secure counter mode cipher is applied both before and after the multiplication, different messages with the same initial value for this weak counter (and, therefore, different starting values for the other counter) are not detectable.
Two other weaknesses might be considered.
What about an attack involving 2^64 messages with chosen plaintexts such that the sums and lengths of all those plaintexts are identical? Wouldn't that help, somehow, in a birthday attack against only half of the initialization vector?
The modified decorrelation used here discards non-decorrelated information in the other block that is involved in the process so that the multiplicative function doesn't have to be invertible. Doesn't this leak information somehow?
Neither of those weaknesses look promising. One can't just change single bits in blocks to probe for information without being faced with a completely different pair of initial counter values.
But this is just a handwaving argument, showing that the obvious frontal attacks on the cipher are blocked. It is not a proof that any existential forgery implies the block cipher is broken.
Dividing existential forgeries into two cases, those where the two checksums being fed into encryption, and the two blocks of the initialization vector are the same in the forgery as in an existing known-plaintext or chosen-plaintext message, and those that are not, as was done in the beginning of the argument above, is at the heart of the proof of security for one of the encryption modes proposed by recognized researchers described in previous sections.
Since the counter used in this cipher has a 256-bit state, if the four AES encryptions which serve as overhead operate with a 256-bit key different from the 128-bit key used for the main part of the cipher, another question is whether the result has an effective 384-bit key, or whether it remains vulnerable to attacks of order 2^128. Even if the mode is secure, and provides essentially free message integrity, attempting to use it to obtain a free increase in key length may prove to be insecure.
Next
Chapter Start
Skip to Next Chapter
Skip to Next Section
Table of Contents
Main Page