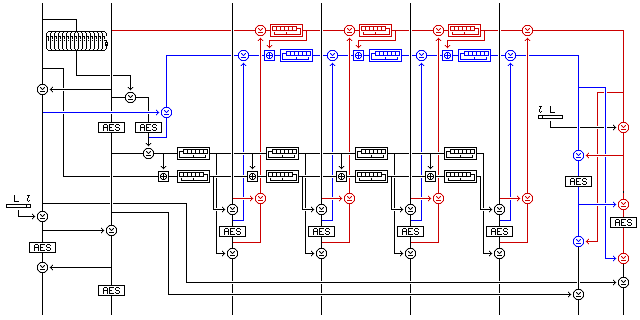
The following diagram illustrates a further attempt of mine at an integrity-aware encryption mode.

This short diagram illustrates the most basic case of the mode. This longer diagram illustrates the mode more fully, including all the possible options it provides:
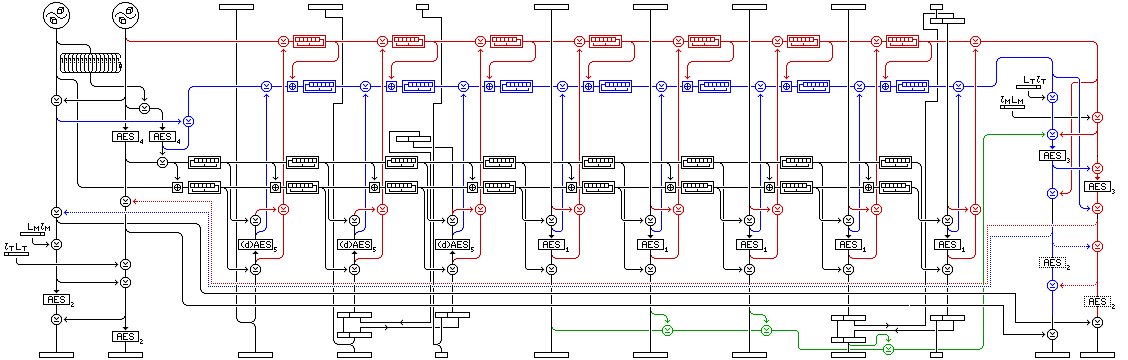
This diagram illustrates five extra things about the mode in the most general case.
Note that although information about the length of the message and the tag field are embedded in the mode, to provide protection against forgeries, the message itself does not provide this information.
The length of the transmitted message as a whole, as well as the length of the tag field and the length of the message as a whole, can be sent as side information without any integrity check, since the integrity checking of the message will validate these parameters of the message.
Their format is not specified, since in some applications the length of the tag field will be known to be zero, and in others all messages will have a fixed format.
It is permissible to embed this information in the protected tag field in an agreed-upon format for a given application as well, but as noted, the protection this provides is not required.
Also note that, although this is not illustrated in the diagram, if the initialization vector and the integrity check are jointly encrypted, the encrypted initialization vector, instead of being transmitted at the beginning of the message, is transmitted immediately before the integrity check, so that its calculation will not delay the transmission of the message. (It will delay its decryption, but as the security of this mode against forgeries requires that the plaintext of messages which fail the integrity check not be displayed to parties not entrusted with the keys, this does not actually add a delay to communications.)
The intent of this mode is to provide an integrity-aware encryption mode that does not require an understanding of advanced mathematics such as Galois field arithmetic to implement, which requires, in addition to the minimum of one block cipher operation per block of message, a fixed number of additional block cipher operations (which is larger than the number required by some other proposed modes), and some simple arithmetic and logical operations for each block of message.
As well, the messages come with a 256-bit initialization vector, and their integrity is protected by a 256-bit field, so that a birthday attack on the integrity check is of the same order of difficulty, 2^128, as a brute-force attack on the underlying block cipher.
Many of the basic concepts of this mode are similar to those of the existing XECBS-XOR proposal, as well as other proposed integrity-aware encryption modes.
Each message enciphered in this mode is accompanied by two blocks of random data that is kept secret. The random bits are sent with the message, but only in an encrypted form.
Two blocks, rather than one, are used for three reasons.
The two random values are used to produce two random starting points for two counters. They are also used to produce two initial values for two checksums.
The first of the two counters is initialized with a value that is guaranteed to be nonzero.
This first counter is stepped by means of a shift register involving a left shift in Galois configuration. This ensures that the first counter has a period of 2^128-1 blocks without repetition. Messages sent in this mode are limited to 2^121-1 blocks due to the format of the length field. (Slight changes to the rules governing that field could allow messages of up to 2^121 blocks and 127 bits in length to be sent.) This limit applies separately to both the tag segment and the encrypted message segment of a message.
The second counter accumulates values of the first counter through modulo 2^128 addition, and then also experiences a shift register step from the encryption of one block to the next. Thus, its values do not relate in a simple, linear fashion to each other, and, because the starting point of the first counter is not sent in the clear, the relationship between successive values of the second counter is not known in advance of cryptanalysis.
The second counter is, however, still just a counter. It is not a secure keystream generator; it simply avoids being trivially linear and predictable.
Two 128-bit checksums are formed as each block is encrypted. Shift register steps involving shifts in opposite directions are used to ensure that moving a block from one location to another in a message has an effect on the checksum.
The two blocks of the initialization vector are jointly encrypted, so that a birthday attack on individual halves of the initialization vector is forestalled, and the two blocks of the final integrity check are also jointly encrypted. The method used is a simple one which would not provide security above that of two isolated block encryptions in the known-plaintext case, but it is satisfactory because it is being applied to values which are internal to the encryption process.
Optionally, the integrity check and the initialization vector can be jointly enciphered; this would provide additional security by hindering an attempt to find messages, other than messages with identical text, that have the same initialization vector. However, an identical initialization vector can also be detected when both plaintext and ciphertext match in two messages, and this can also lead to detection of cases where the state of the two counters is repeated, possibly at a different position in a message. This latter case, however, will not help in determining the initial state of the two checksums which must be matched to accomplish even an existential forgery.
Also note that, since the method is intended to protect against forgery, only chosen plaintext attacks, not chosen ciphertext attacks, are available; thus, the secondary counter is applied to the plaintext on input to the block cipher. Since the tag field is treated as ciphertext, and is also subject to choice, the use of the two counters is reversed for the tag field, which is otherwise treated as if it were ciphertext.
For some implementations, deciphering in addition to enciphering with a given key would involve overhead similar to that required for using more than one encryption key. Because this might be an excessive overhead in some cases, the option is provided for using AES encryptions instead in modifying the running checksums in response to the tag field where AES decryptions would be required to treat the tag field as identical to ciphertext.
In this case, the sequence of operations to which tag field contents are subjected is identical to that to which plaintext is subjected; first an XOR with the second counter, then an encryption, then an XOR with the first counter. But different elements from the process are used in producing the checksum, at points analogous to producing the tag field from encipherment.
If it were not for the fact that the length of the initialization vector protects it from birthday attacks, and that the checksum is encrypted before being used as an integrity check, this could conceivably lead to attacks based on choosing, as plaintext, a message identical to a previous message, except with the first block of plaintext replaced by an additional block of the tag field, containing the ciphertext corresponding to that plaintext. It is because this option does not lead to a genuine compromise of security that it is provided, although it is preferred to use the decryption operation where possible.
As well, although the XOR and shift-register operations for the counter and the checksums need to be performed serially, the time-consuming block cipher operations can be paralellized in this mode.
The block cipher mode described here, and termed double-counter double-checksum mode, provides integrity checking for a tag field which may be either 0 bits in length (that is, not used), or from 128 bits in length to 2^128 bits in length, and encryption and integrity checking for a message field which may either be 0 bits in length (that is, not used), or from 128 bits in length to 2^128 bits in length.
The authorized decryptor of a message must know the lengths of the tag field and the message field of any given message; no means of conveying this information is specified as part of this mode, since the mode inherently protects this information from falsification, and since what portion, if any, of this information is required to be transmitted with a given message is application-dependent.
The tag field will be considered to consist of 128-bit blocks T(1), T(2), T(3).... T(NT), and the message will be considered to consist of 128-bit blocks M(1), M(2), M(3)... M(NM). In addition, either or both of the tag and message fields may include a final short block, TP for the tag field, and MP for the message field. NTB equals either NT or, if a partial tag block is present, NT+1; NMB equals either NM or, if a partial message block is present, NM+1.
Up to five encryption keys may be used with this mode, K(1) through K(5). When less than five encryption keys are used, and the given keys are GK(1) through GK(NK), then K(1) through K(NK) are equal to GK(1) through GK(NK) respectively, and K(NK+1) through K(5) are equal to GK(1). Thus, if two keys are given, K(1) is the first of them, K(2) is the second of them, and K(3) through K(5) are all set equal to K(1).
E(x,k) is, of course, defined as the block produced by applying AES with key k to the block x, and D(x,k) is defined as the block produced by decrypting block x using AES with key k.
The process of applying this mode begins with the generation of two random 128-bit blocks, R(1,0) and R(2,0). The second subscript is used to distinguish the original values of these blocks from later values derived from them.
They are used to supply initial values for the two counters, C(1,0) and C(2,0), and initial values for the two checksums, S(1,0) and S(2,0), as follows:
S(1,0) is set to the value of R(2,0).
C(2,0) is set to the value of R(1,0).
nonzero(R(1,0)) is calculated. This value is defined as the first fifteen bytes of R(1,0), followed by the bitwise negation of the single byte XOR of these first fifteen bytes. If those first fifteen bytes are all zero, this last byte will be 11111111 in binary, and thus this function is guaranteed to be nonzero.
R(1,1) is calculated as the XOR of R(1,0) and R(2,0).
R(2,1) is calculated as E(R(2,0),K(4)).
The temporary value T(1) is calculated as E(R(2,0) xor nonzero(R(1,0)),K(4)).
C(1,0) is set to R(2,1) xor T(1). Since R(2,0) is guaranteed to be different from R(2,0) xor nonzero(R(1,0)), and since E(x,K(4)), the block cipher AES with key K4, is bijective, C(1,0) is guaranteed to be nonzero.
S(2,0) is set to R(1,1) xor T(1).
The process of encrypting the two random values which form the initialization vector for transmission proceeds as follows.
R(1,2) is normally set to R(1,1); it may be set to R(1,1) xor II(1,5), to be defined later, if joint encryption of the initialization vector and the integrity check is selected.
R(2,2) is normally set to R(2,1); it may be set to R(2,1) xor II(2,5), to be defined later, if joint encryption of the initialization vector and the integrity check is selected.
R(1,3) is R(1,2) xor the concatenation of the number of whole blocks in the message field, as a 121-bit unsigned binary integer, and the number of bits in the partial block at the end of the message field, or zero if there is no partial block, as a 7-bit unsigned binary integer.
R(2,3) is R(2,2) xor the concatenation of the number of bits in the partial block at the end of the tag field, or zero if there is no partial block, as a 7-bit unsigned binary integer, and the number of whole blocks in the tag field, as a 121-bit unsigned binary integer.
R(2,4) is R(2,3) xor R(1,3).
R(1,4) is E(R(1,3),K(2)).
R(1,5) is R(1,4) xor R(2,4).
R(2,5) is E(R(1,4),K(2)).
The encrypted initialization vector to be transmitted will consist of R(1,5) followed by R(2,5). These will be the first two blocks sent, unless joint encryption of the initialization vector and the integrity check is selected; in that case, the encrypted initialization vector will be transmitted after the tag field and the encrypted message field, and before the integrity check.
Advancing the two counters used to mask the block cipher operation used for both encryption and integrity checking of the message field and integrity checking of the tag field is performed as follows:
Given C(1,i) and C(2,i), C(1,i+1) and C(2,i+1) are produced by these steps:
C'(2,i) is set to the sum, modulo 2^128, of C(2,i) and C(1,i), where each is considered to be a 128-bit unsigned binary integer.
C(1,i+1) is equal to C(1,i) shifted one place to the left, and, if the bit shifted out of the leftmost position is a 1, XORed with the hexadecimal value
5555 54AA AAAA AA55 5555 5555 5555 1115
chosen to approximate a simple pattern of alternating bits, while still corresponding to a primitive polynomial.
C(2,i+1) is equal to C'(2,i) shifted one place to the right, and, if the bit shifted out of the rightmost position is a 1, XORed with the hexadecimal value
9550 4884 A150 8908 4851 0848 94A1 0848
in which the spacing between powers used in the polynomial which the value represents is derived from the base four expansion of Euler's constant, except for the lowest-degree terms in the polynomial, which are altered to make it primitive.
A block of the tag field, that is neither the last block if it is a partial block, nor the whole block immediately preceding a partial block, is protected by means of the following steps applied to that block itself (the steps involving the checksums will be described below):
TI(i,1) is the XOR of T(i) and C(2,i).
TI(i,2) is either D(TI(i,1),K(5)) or E(TI(i,1),K(5)). The latter involves less overhead when K(5) equals K(1), but in that case the former may be slightly more secure.
TI(i,3) is the XOR of T(i) and C(1,i).
For purposes of modifying the checksums, U(i) is equal to TI(i,1) xor TI(i,3), and V(i) is equal to TI(i,2).
As the tag field is not encrypted, it the original values T(i) are the ones sent with the message.
When a partial block is present in the tag field, ciphertext stealing is carried out as follows:
T'(NT+1) is formed from the concatenation of TP and the last 128-length(TP) bits of T(NT).
T'(NT+1) is then subjected, for i equal to NT+1, to the process described above for the T(i) values corresponding to unaffected whole blocks.
T'(NT) is formed from the concatenation of the first length(TP) bits of T(NT) and the last 128-length(TP) bits of TI(NT+1,3).
T'(NT) is then subjected, for i equal to NT, to the process described above for the T(i) values corresponding to unaffected whole blocks.
A block of the message field, other than the last block of the message, if it is partial, and, in one minor respect, the whole block immediately preceding the final partial block, is encrypted by means of the following steps:
MI(i,1) is the XOR of M(i) and C(2,i+NTB).
MI(i,2) is E(MI(i,1),K(1)).
X(i) is the XOR of MI(i,2) and C(1,i+NTB).
For purposes of modifying the checksums, U(i) is equal to M(i) xor MI(i,2), and V(i) is equal to MI(i,1).
The values X(i) constitute the encrypted text that is to be transmitted.
When a partial block is present in the message field, ciphertext stealing is carried out as follows:
The last full block, M(NM), is encrypted as described above for unaffected message blocks M(i) for i equal to NM, but X'(NM), the formation of which will be described below, instead of X(NM), is transmitted with the message.
M'(NM+1) is formed from the concatenation of MP and the last 128-length(MP) bits of X(NM).
M'(NM+1) is then encrypted using the process described above for unaffected message blocks M(i) for i equal to NM+1, but X(NM+1) is not transmitted with the message as an unbroken block.
X'(NM) is formed from the first length(MP) bits of X(NM) and the last 128-length(MP) bits of X(NM+1), and is transmitted with the message, followed by the first length(MP) bits of X(NM+1).
The process of updating the checksums on which the integrity check is based proceeds as follows:
CI(1,i,1) is the XOR of C(1,i-1) and U(i). (Note that U(i) can come from either protecting a tag field block or encrypting a message field block, and the U(i) values produced from the processing of partial blocks and the blocks that precede partial blocks are included.)
C(1,i) is C(1,i,1) shifted one place to the right, and, if the bit shifted out of the rightmost position is a 1, XORed with the hexadecimal value
A548 8080 8080 8080 8080 8080 8080 8080
CI(2,i,1) is the XOR of C(2,i-1) and V(i). (As for the U(i) values, these are produced from whole or partial tag or message blocks.)
CI(2,i,2) is the sum, modulo 2^128, of CI(2,i,1) and C(1,i).
C(2,i) is CI(2,i,2) shifted one place to the left, and, if the bit shifted out of the leftmost position is a 1, XORed with the hexadecimal value
1040 4080 1001 0404 2008 2040 8020 0A81
which is derived from the octal expansion of pi, but adjusted to correspond to a primitive polynomial.
The final checksum values, C(1,NTB+NMB) and C(2,NTB+NMB), are encrypted as follows for transmission with the message:
II(1,1) is set to C(2,NTB+NMB).
II(2,1) is set to C(1,NTB+NMB).
II(1,2) is the XOR of II(1,1) and the concatenation of the number of whole blocks in the tag field, expressed as a 121-bit unsigned binary integer, with the number of bits in the last partial block of the tag field (or 0, if no partial block is present), expressed as a 7-bit unsigned binary integer.
II(2,2) is the XOR of II(2,1) and the concatenation of the number of bits in the last partial block of the message field (or 0, if no partial block is present), expressed as a 7-bit unsigned binary integer, with the number of whole blocks in the message field, expressed as a 121-bit unsigned binary integer.
II(1,3) is the XOR of II(1,2), II(2,2), and, optionally, the XOR of all whole transmitted encrypted blocks corresponding to the whole blocks of the message field only, as an additional security measure against chosen plaintext attacks.
II(1,4) is E(II(1,3),K(3)).
II(2,3) is the XOR of II(2,2) and II(1,4).
II(2,4) is E(II(2,3),K(3)).
II(1,5) is the XOR of II(1,4) and II(2,1).
II(2,5) is the XOR of II(2,4) and II(1,1).
Note that the preceding two steps mean that the operations performed on II(1,1) and II(2,1) are not invertible.
If joint encryption of the initialization vector and the integrity check is not specified, then II(1,7) is equal to II(1,5) and II(2,7) is equal to II(2,5).
If joint encryption of the initialization vector and the integrity check is specified, then an additional invertible encryption step is performed on II(1,5) and II(2,5), used in modifying the initialization vector in that case, as follows:
II(2,6) is the XOR of II(2,5) and II(1,5).
II(1,6) is E(II(1,5),K(2)).
II(1,7) is the XOR of II(1,6) and II(2,6).
II(2,7) is E(II(2,6),K(2)).
Whether or not joint encryption of the initialization vector and the integrity check is specified, the process of preparing the integrity check for transmission concludes as follows:
I(1) is the XOR of II(1,7) and R(2,2).
I(2) is the XOR of II(2,7) and R(1,2).
I(1) and I(2) constitute the two-block integrity check to be sent with the message.
It can be seen fairly simply that this mode is a valid method of encrypting data.
The counter values used as a wrapper for the actual message encryption depend only on the random IV generated internally; they do not depend in any way on the message contents. As a result, in the absence of the integrity check, the encryption is secure if electronic codebook mode encryption is secure.
Does the integrity check compromise the security of the mode? The raw integrity check blocks are both subjected to the block cipher used for encryption before being transmitted. The XOR of the raw blocks, which produces a masking making the operation a non-invertible hash function, does so without leaking information about the raw blocks, because each raw value is XORed with an encrypted block cipher output.
Allowing the assumption that the underlying block cipher is secure, does the ability to create an existential forgery with this mode contradict that assumption? This is what a formal proof would require; what follows is not a full formal proof, but does indicate portions of what one might contain, as well as giving security-related reasons for some of the design decisions in this mode.
An existential forgery, in the case of the block cipher being secure, would need to involve no novel AES encryptions. Each AES encryption would have to have been one encountered in a preceding actual message. This is true despite the fact that in an existential forgery, one does not care about the content of the encrypted message, because all these potential "don't care" values are included in both of the two checksums that enter into the encrypted integrity check. The input and the output of every AES operation in this mode enters in some way into the computation of an output block, as can be seen by inspection of the diagram showing how the mode operates.
Could an existential forgery still involve a novel initialization vector value, by having the AES encryptions that encrypt the initialization vector match those in some other portion of a previous message with known or chosen plaintext?
Although it is believed that having known or chosen plaintext will not actually allow one to determine the actual input and output to any AES operation performed in producing that message, this cannot be assumed. If we do not make this assumption, is this kind of forgery impossible?
To accomplish this, one would have to choose two output values for the final two AES encryptions in that process such that the input values would lead to the two AES encryptions involving the original second half of the initialization vector, and the AES encryption involving that XOR the nonzero function of the first half of the initialization vector, both being non-novel. Since this is a new combination of encryption operations, there is no a priori reason for such a match to exist.
The probability of being able to obtain such a match for a given pair of codebook entries equals the square of the fraction of the possible 2^128 block values that are in one's codebook. Since one can use any two items in one's codebook in an attempt to achieve such a match, its probability is equal to the fourth power of the number of items in one's codebook divided by 2^256.
Thus, with a codebook approaching 2^32 entries in size, this might be possible.
But one then has a novel set of initial values for the two checksums and for the two counters which is strictly determined by the coincidence one has found. These have to lead to at least one block encryption for either a message field or a tag field, and two block encryptions in the integrity check, that are non-novel.
Because one can arbitrarily choose the message contents, it is potentially possible to make all but the last two block cipher operations non-novel directly.
This determines two independent checksums, which need to lead to the final two block cipher operations being non-novel.
This clearly becomes easier the longer the message one wishes to forge is, since from one's pool of codebook entries, more possible values can be produced. With a codebook of 2^32 entries, a message containing six blocks lets one produce 2^192 combinations for the last two blocks, enough to find one for which both encryptions are in the codebook.
Thus, if there is some method to form a codebook of encryptions from known or chosen plaintexts, this mode would not be secure against piece-by-piece construction of a forged message if more than about 2^16 messages are sent with a single key.
It is, of course, unclear that this is possible. The random initialization vector used is never sent in the clear, and it is used to produce a counter whose values, and the relations between the values for half the counter, are unknown, and used to mask the encryption operations in the message body for which the input and output could both become known.
If the existential forgery uses the same initialization vector as an existing message with known or chosen plaintext, then there are a number of possibilities to enumerate.
Truncating a block from the end of a message leads to the encryptions which form the integrity check being novel with overwhelming probability.
The same applies to adding a block to the end of a message, but if one has a codebook, one might be able to search for possibilities.
Interchanging two blocks in a message, with suitable adjustments to them to make the encryptions correspond for the changed counter values, will also alter the checksums. This is despite the fact that the checksums and the counter are similar in structure, and there is a 6.25% probability that the differing primitive polynomials in the shift registers will not be invoked at all. This is because of the presence of an accumulating checksum among the two checksum blocks. This accumulating checksum will now see one fewer occurrence of one of the two blocks, and one more occurrence of the other, if the two blocks are adjacent.
What appears to be the weakest link of this cipher against an existential forgery is the possibility of taking an existing message, and then sending one which is substantially similar, except that the tag field in the new message is expanded to include the first block of the message field in the old message. But this results in the final two encryptions used to protect the initialization vector having to be novel, as a minimum consequence, because the length information to the message is placed in that part of the process. The encryptions which protect the integrity check would also be novel for the same reason. If the operation used for the tag field is an encryption, although this makes it easy to produce a non-novel encryption without having to have an explicit codebook, because the values entering into the checksum are taken in a different order, that is changed. If a decryption is used instead, as recommended, the reversed order in which the counters are used forces the use of a codebook to find a matching block value; the fact that the intermediate results now enter into the checksums in the same order, relative to the sense of the encryption operation, is made difficult to exploit because the mask values are wrong.
What would, however, give a tighter bound on the security of this mode is some way to determine the difficulty of obtaining useful codebook entries from known or chosen plaintext. An accumulating counter, with an unknown starting point, appears to eliminate some potential attacks on the mode, but can one be sure it does not merely complicate them slightly? Consistently placing the accumulating counter in the path preceding the encryption, where an attacker might choose tag field values and plaintext, precludes a birthday attack aimed at making the encryption of identical blocks detectable by a shift-register pattern in the output. A pair of blocks in chosen plaintext can, however, be chosen so as to make one particular value in the first counter visible, even when the initial value of the second counter is unknown. So the fixed relationship of items in the first counter can be exploited, but because this exploitation only works for one value of the first counter at a time, one does not even have a birthday attack. That this exploitation obtains a codebook for the initialization vector is not particularly useful, because there are 2^256 entries, rather than 2^128, to accumulate. Its real danger is that it allows an extract from the codebook for the encryption operation to be formed, although that extract is displaced by an unknown amount, and that amount transformed for successive items, due to the unknown starting value for the accumulating counter.
If a codebook with 2^32 entries is dangerous to this mode, were it the case that it requires 2^128 effort to obtain any codebook entries would mean that this mode provides as much security against an existential forgery as the underlying block cipher itself provides against reading messages. Then, this mode would achieve its ambitious goal of providing a free integrity check fully as secure as the underlying cipher, which is not met by modes with only a single block used for the initialization vector and the integrity check.
Given that "whitening", as used with DESX, is generally thought to be a valid means of increasing the key length, it would seem that this mode might provide a means of increasing the keyspace over which brute force would be required to read messages without increasing the time required to encrypt each block of the message.
Even if this is true, there is at least one limitation to this.
If one knows the plaintext of the first two blocks of a message, and wishes to read the rest of the message, then one can always do so with a brute-force search of order at most 2^256, even if K(1), K(2), and K(4) are all independent. This is because once you have assumed a value for K(1), and for one of the two counters, the value of the other counter required for a given plaintext/ciphertext pair can be derived directly.
Adding four 128-bit blocks to every message might be felt to be excessive.
One way to reduce this to two 128-bit blocks might seem to be the following: form an integrity check, two blocks in length, that depends only on the transmitted blocks, not the initialization vector. Then, combine that with the initialization vector.
The decryptor would then compute the integrity check from the message, and deduce the initialization vector. After using that to decrypt the message, however, the message would have to be accepted. An integrity check that depends on both plaintext and ciphertext would, necessarily, depend on the initialization vector if one was used.
Getting the initialization vector wrong would, though, guarantee a garbled message, which is another form of integrity awareness, even if less strong than security against existential forgery.
Next
Chapter Start
Skip to Next Chapter
Table of Contents
Main Page