In some ways, the cipher systems outlined in this chapter are disappointing, compared to what we had seen in the previous chapter.
This reflects the difficulty of manipulating binary signals with simple electromechanical devices, and it may also involve the psychological effect of overconfidence in the security of a system based on new and unfamiliar principles.
The M-228 is an exception to both halves of this generalization; it is secure, but it isn't entirely new, being largely based on a rotor mechanism.
Of course, it is true that I could have described the T-52 in more detail (at least in words, for those who cannot recieve the schematic diagrams included in that section, which do accurately describe it). It is certainly very complex. But the complexity and expense of the machine are beyond those of the SIGABA, while the security may well be less even than that of the Enigma. (Yes, it was broken less often than the Enigma; but there were fewer intercepts, and the more restricted distribution of the machine makes it likely that it was more carefully used.) Had the routing of signals to the various inversion and swapping relays changed with every character, instead of merely being a static part of the key, the system might have been significantly more secure. Of course, even more important would be the change to pinwheels instead of cams.
It is interesting that one wire in the Swedish SA-1 seems to hold the key to the security of that machine. That wire is the one from the first pinwheel bank which controls the stepping of the second pinwheel bank. But can something that contains only a single bit of information per five-bit character really provide security?
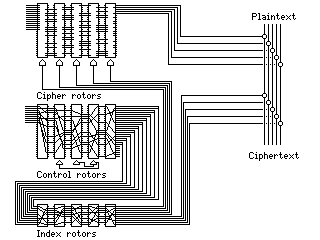
The M-228 is interesting, and as noted in the section on it, apparently a newer machine existed that was like a SIGABA, except that the cipher rotors were used to encipher teletypewriter signals in the fashion of the M-228.
The following diagram:

illustrates an interesting idea for taking that concept even further. The cipher rotors work like the old M-228, in order to XOR the message with unbiased individual bits. The control rotors are also simplified, so that they can produce five extra signals, which are also XORed with the message.
This appears to strengthen the machine, since bits from two essentially independent sources are XORed with the plaintext. Can we be sure that the bits from the cipher rotors completely mask those from the control rotors, though, or could this design have a weakness, by offering a "window" to the control rotors?
However, while the SZ-40 and the TC-52 may have had their weaknesses, the SA-1 showed that despite the relatively simplistic nature of this kind of telecipher machine, that approach has at least some life in it. Thus, a construction like the one below:
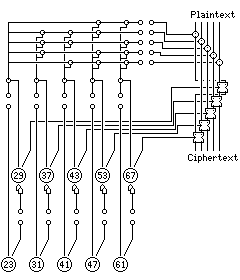
with still only ten pinwheels, but including a smaller version of the TC-52 relay bank, and three plugboards, might offer some security.
In the diagram, the two sets of five pinwheels supply bits which are XORed together, and then which are mixed together in a relay bank before being XORed with the plaintext. The relay bank must correspond to an invertible matrix to ensure all 32 possible values can be XORed with the plaintext.
The second tap from the first set of five pinwheels controls the double stepping of the pinwheels in the second set; the second tap from the second set of five pinwheels is used to control bit swapping.
A further extension of this design can run as follows:
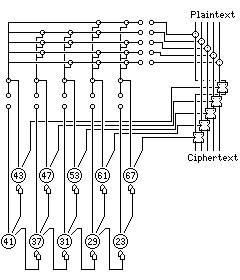
Here, the first bank of pinwheels are all smaller than the second bank; this ensures, since the sizes of the pinwheels in the second bank are all prime, that the number of active pins in the pinwheels in the first bank must be relatively prime to the sizes of the pinwheels whose movements they control.
Only two plugboards are present, but note that a second tap has been added to four of the five pinwheels in the first bank, so that they control each others' movements.
Here, larger pinwheels control smaller ones, but since each pinwheel controls the next smaller, as long as the number of active pins is about half the total, again that number is relatively prime to the size of the pinwheel controlled.
Of course, since it is double stepping the pinwheels are controlling, it is not really the number of active pins that needs to be compared.
If the 41 pinwheel had only two active pins, then as 41 characters are enciphered, the 43 pinwheel would step once 39 times and it would step twice 2 times, thus eliminating a factor of 43 from the period.
The 37 pinwheel would have to have 10 active pins, and the 31 pinwheel would have to have 22 active pins, to encounter this sort of problem; the 29 and 23 pinwheels are both too small, being less than half the size of the pinwheels they control.
Just as 2 is very far from half of 41, 10 is much smaller than half of 37, and 22 is much larger than half of 31, so again, staying out of trouble is not too difficult. Of course, having five pinwheels arranged so that each one controls the next involves five time delays, which poses its own design problems, but the result is a very irregular sequence of bits.