Main : Index : The Computer Era : Quadibloc : Quadibloc 2002

Quadibloc 2002

Quadibloc 2002 is a block cipher designed to incorporate the ideas introduced in several of the other ciphers in the Quadibloc series.

This diagram illustrates the Quadibloc 2002 round.

It has some resemblance to the round in Quadibloc XI.

In addition to embodying the principle of indirection, as illustrated in Quadibloc IX and Quadibloc XI, it uses bit swaps which, by directing bits between inputs which were formed through different algorithms to outputs which are used for different purposes, make the cipher's algorithm variable in a data-dependent way, recalling Quadibloc III and VIII, but without creating vulnerability to timing or power consumption monitoring attacks, and it uses pools of subkeys as did Quadibloc VII; also, the distinction between the input to a Feistel structure and its subkeys is employed in a manner reminiscent of Quadibloc IV.

Thus, it can be said to sum up the lessons learned from the Quadibloc series of ciphers, except that I never seemed to learn the lesson that ciphers should be simple and fast rather than large and elaborate.

Because the elaborate f-function of this cipher only modifies 32 bits of the 128-bit block, diffusion is slow enough that 16 rounds are required.

Round Overview

In a Quadibloc 2002 round, the 128-bit block is considered to be divided into four 32-bit subblocks.

First, the leftmost subblock is changed by alternately applying two different transformations, one three times and the other two times. This leads to that subblock having four intermediate values, which are used in other parts of the round.

Then, the second and third subblocks are used as input to a form of the standard Quadibloc f-function. The two intermediate results are also used; in one case, the second one is XORed with the input to the f-function (the value of the second subblock) and in the other case, the first one is XORed with the final f-function output.

The first of the intermediate values of the first subblock is used to select subkeys from subkey pools for these f-functions, as well as for some of the later manipulations. Because of this, the first subblock must be transformed before the two f-functions are performed, the reverse of the order required by some of the variations of Quadibloc XI, such as Quadibloc XI HD.

The intermediate result values are then transformed, using operations similar to those used on the first subblock. In one of them, instead of using the constant S-box S4, key-dependent S-boxes S8 and S9 are used.

This leaves us with six values; for each of the second and third subblocks, an f-function output, and two scrambled intermediate results. The algorithm used to scramble the first intermediate result of the second subblock is used to scramble the second intermediate result of the third subblock, to create an additional degree of diversity in the algorithms which produced each value.

The second intermediate value of the first subblock is then used to control an ICE-style bit swap, between the scrambled first intermediate result of the second subblock and the f-function output of the third subblock. The two outputs of this bit swap are each used to control two further bit swaps, one between the f-function output of the second subblock and the scrambled first intermediate result of the third subblock, and the other between the two scrambled second intermediate results (but each one is scrambled by a different algorithm, and only one second intermediate result was XORed with the initial input).

These four results, together with the third and fourth intermediate values of the first subblock, are used to produce the f-function output of the round as a whole by means of two four-round Feistel structures. The first of the last two bit swaps directed bits between the subkeys of the first two rounds of the first structure and the input to the second structure; the second of those bit swaps directed bits between the input to the first structure and the subkeys of the last two rounds of the second structure. The two intermediate results were used as subkeys for the last two rounds of the first structure, and the first two rounds of the second structure.

The outputs of the two Feistel structures are then applied to the fourth subblock using a combiner similar to that used with Quadibloc XI, in which each 32-bit input is used as subkeys for four small-scale Feistel rounds that produces subkeys for two small-scale Feistel rounds acting on half of the 32-bit subblock.

Because of the heavy use of key-dependent S-boxes, and because the bit swaps vary the algorithmic function of bits of disparate algorithmic origins, this round is highly resistant to analysis.

After each round except the last, subblocks are interchanged using the same tire-rotation pattern as in Quadibloc XI.

The Rounds In Detail

The 128-bit block to be enciphered is split into four 32-bit subblocks for the purposes of this block cipher.

The first, or leftmost, subblock is subjected to five transformations.

The first transformation proceeds as follows:

The 32-bit subblock is split into a 16-bit left half and a 16-bit right half.
The right half is modified by being XORed with an f-function of the left half. This f-function is calculated as follows:
- A copy of the left half is XORed with the left half of subkey K1 (in the first round, K8 in the second round, and so on, to K106 in the sixteenth round).
- The left-hand byte of the result is used as an index into key-dependent S-box S10.
- The right-hand byte of the result is used as an index into key-dependent S-box S11.
- The values found in S10 and S11 are added together using modulo 65,536 addition. The result is the value of the f-function.
The left half is modified by being XORed with an f-function of the right half. This is the same f-function as previously used, but in this case the right half of subkey K1 is XORed with a copy of the modified right half of the subblock to begin.

The value of the leftmost subblock after this transformation is the first intermediate value.

The second transformation proceeds as follows:

The 32-bit subblock is divided into a left and right half, each 16 bits long.
The right half of the subblock is modified by being XORed with an f-function of the left half, calculated as follows:
- The input to the f-function (a copy of the left half of the subblock) is split into its left and right bytes.
- The right byte is modified by being XORed with an f-function of the left byte, calculated as follows:
  - The input to the f-function (a copy of the left byte) is XORed with the leftmost, or first, byte of subkey K2 (in the first round, K9 in the second, K107 in the sixteenth).
  - The result is used as an index into S-box S4, which is the S-box designated as S4 in the page on Euler's Constant and the Quadibloc S-boxes.
  - The value found in S4 is the output of the f-function.
- The left byte is then modified by being XORed with the same f-function of the modified right byte, except that the second byte of subkey K2 is XORed with the copy of the input to the f-function at the beginning.
The left half of the subblock is then modified by being XORed with the same f-function of the modified right half as was originally used in the other direction, except that the third and fourth bytes of subkey K2 are used in place of its first and second bytes in the two internal f-functions.

The value of the leftmost subblock after this transformation is the second intermediate value.

The third transformation is identical to the first transformation, except that subkey K3 (K10, K17... K108) is used instead of K1.

The value of the leftmost subblock after this transformation is the third intermediate value.

The fourth transformation is identical to the second transformation, except that subkey K4 (K11, K18... K109) is used instead of K2.

The value of the leftmost subblock after this transformation is the fourth intermediate value.

The fifth transformation is identical to the first transformation, except that subkey K5 (K12, K19... K110) is used instead of K1.

The value of the leftmost subblock after this transformation is the value on exit from the round.

The second and third subblocks are not modified by the round, but they are used as inputs to a calculation, along with the first two intermediate values of the first subblock, which produces six values which are then used to derive four values, which along with the second two intermediate values of the first subblock to calculate two 32-bit values which are used to modify the fourth subblock.

The process for deriving three values from the value of the second subblock proceeds as follows:

A copy of the value of the second subblock is used as input into a version of the standard Quadibloc f-function. This function proceeds as follows:

The input into the f-function, a copy of the second subblock, is XORed with the value from subkey pool SP1 (in the first round, SP9 in the second, SP17 in the third, to SP121 in the sixteenth round) indicated by the first or leftmost nybble of the first intermediate value of the first subblock.
The result is divided into four bytes. These bytes are then replaced by their substitutes found in S-boxes S1, S1, S1, and S2 respectively, where S1 and S2 are the constant S-boxes derived from Euler's constant so designated on the page previously mentioned in connection with S-box S4.
The bits of the result, considered to be numbered from 1 (most significant bit of the first, leftmost byte) to 32 (least significant bit of the last, rightmost byte) following the pattern in DES, are to be transposed to lie in the following positions:

 1  2 27 28 21 22 15 16
 9 10  3  4 29 30 23 24
17 18 11 12  5  6 31 32
25 26 19 20 13 14  7  8

The current value of the result is the first intermediate result (of the second subblock).
The result is XORed with the value from subkey pool SP2 (in the first round, SP10 in the second, SP18 in the third, to SP122 in the sixteenth round) indicated by the second nybble of the first intermediate value of the first subblock.
The result is divided into four bytes. These bytes are then replaced by their substitutes found in S-boxes S1, S2, S2, and S2 respectively, where S1 and S2 are the constant S-boxes derived from Euler's constant so designated on the page previously mentioned in connection with S-box S4.
The bits of the result are transposed according to the transposition previously described.
The current value of the result is the second intermediate result (of the second subblock).
The result is XORed with the value from subkey pool SP3 (in the first round, SP11 in the second, SP19 in the third, to SP123 in the sixteenth round) indicated by the third nybble of the first intermediate value of the first subblock.
The result is divided into four bytes, each of which is then replaced by its substitute found in the key-dependent S-box S8.
The current value is the output from the f-function.

The first temporary value is calculated by forming the XOR of the input to the f-function and the second intermediate result.

The second temporary value is the first intermediate result.

The first temporary value is transformed by means of a transformation identical to the first transformation applied to the first subblock except that subkey K6 is used in place of subkey K1 (and so on for later rounds).

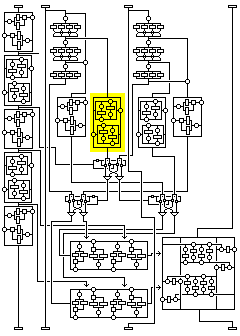
The second temporary value is transformed by means of a transformation identical to the second transformation applied to the first subblock, except that a value obtained by using the fourth nybble of the first intermediate value of the first subblock as an index into subkey pool SP4 is used instead of K2 (a value from SP12 used instead of K9 in the second round, and so on), and with key-dependent S-box S8 used instead of the constant S-box S4.

A similar calculation is then performed on a copy of the value of the third subblock, but with some important differences.

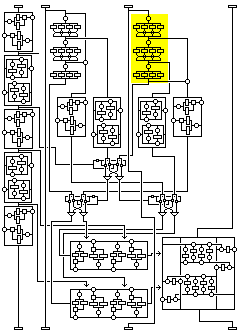
First, it is subjected to the same version of the standard Quadibloc f-function as used with the second subblock. However, the subkeys are different: now, the fifth, sixth, and seventh nybbles of the first intermediate result are used as indexes into SP5, SP6, and SP7 respectively (instead of the first, second, and third nybbles into SP1, SP2, and SP3), again using later subkey pools in later rounds.

The first temporary value is now formed from the second intermediate result of this f-function of the third subblock alone; the second temporary value is the XOR of the first intermediate result and the f-function output.

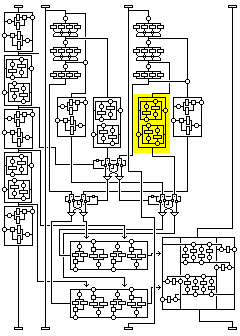
Now, the first temporary value is transformed by means of a transformation similar to the second transformation applied to the first subblock. But instead of K2, the value selected from SP8 by the eighth nybble of the first intermediate value of the first subblock is used, and instead of S-box S4 (or S8), the key-dependent S-box S9 is used.

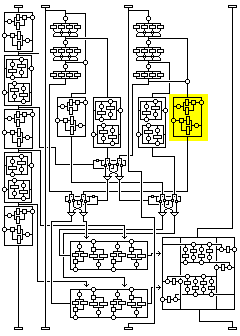
And it is the second temporary value that is transformed by means of a transformation identical to the first transformation applied to the first subblock, except that subkey K7 is used instead of subkey K1.

We now have six values; the f-function output, the transformed first temporary value, and the transformed second temporary value, from the second subblock, and the f-function output, the transformed first temporary value, and the transformed second temporary value, from the third subblock.

The second intermediate value of the first subblock is used to control a bit swap of the type pioneered by the block cipher ICE, wherein bits in the two other inputs corresponding to bits having the value of 1 in this control input are exchanged between them. The two inputs consist of the transformed second temporary value from the second subblock, and the f-function output from the third subblock. The outputs after swapping shall be called the first and second swap outputs (thus, the first swap output consists of those bits of the transformed second temporary value from the second subblock corresponding to zero bits in the second intermediate value of the first subblock, and those bits of the f-function output from the third subblock corresponding to one bits in the second intermediate value of the first subblock).

The first swap output is used as the control word for another ICE-style bit swap, whose two inputs are the f-function output from the second subblock and the transformed second temporary value from the third subblock, and whose two outputs will be the third and fourth swap outputs.

The second swap output is used as the control word for another ICE-style bit swap, whose two inputs are the transformed first temporary value from the second subblock and the transformed first temporary value from the third subblock, and whose two outputs will be the fifth and sixth swap outputs.

These swap outputs, together with the third and fourth intermediate values of the first subblock, are used to calculate the primary f-function value for the round in two 32-bit halves by the following procedure:

Each of the two final 32-bit output values is created by means of four Feistel rounds similar to the two Feistel rounds which made up the first transformation applied to the first subblock.

For the first 32-bit final output value, the input is the fifth swap output, for the first two rounds, K1 is replaced by the fourth swap output, and for the last two rounds, K1 is replaced by the third intermediate value of the first subblock.

For the second 32-bit final output value, the input is the third swap output, for the first two rounds K1 is replaced by the fourth intermediate value of the first subblock, and for the last two rounds K1 is replaced by the sixth swap output.

The two final output values are then applied to the fourth subblock, changing its value, by means of a combiner similar to that seen in some of the later variants of Quadibloc XI.

The application of the final output values to the fourth subblock proceeds as follows:

This transformation consists of two rounds.

In each round, one half of the fourth subblock is used as input to four Feistel rounds, keyed by the input to be combined with the value being modified. The output of those Feistel rounds is then used to supply subkey input to two more Feistel rounds of the same type which modify the other half of the subblock. Thus, the input functions as a subkey in a cipher that produces a subkey.

The first round proceeds as follows:

First, four Feistel rounds are performed to serve as an f-function, enciphering a copy of the first two bytes of the subblock to produce a 16-bit value to be used as a subkey to later modify the last two bytes of the block, as follows:
- A copy of bytes 1 and 2 of the subblock is made.
- Byte 1 of the input is XORed with the copy of byte 1 of the subblock to produce a value used to index into key-dependent S-box S9, without the copy of byte 1 being changed for subsequent use.
- The value selected from S-box S9 is then XORed with the copy of byte 2 of the subblock, changing the copy (but not the original).
- Byte 2 of the input is XORed with the copy of byte 2 of the subblock as modified. The result of this XOR is used as an index into key-dependent S-box S9, while the copy of byte 2 of the subblock is not changed for subsequent use.
- The byte found in S-box S9 in the previous step is XORed with the copy of byte 1 of the subblock, changing the copy (but not the original).
- Byte 3 of the input is XORed with the copy of byte 1 of the subblock as modified. The result of this XOR is used as an index into key-dependent S-box S9, while the copy of byte 1 of the subblock is not changed for subsequent use.
- The value selected from S-box S9 is then XORed with the copy of byte 2 of the subblock as modified.
- Byte 4 of the input is XORed with the copy of byte 2 of the subblock as modified. The result of this XOR is used as an index into key-dependent S-box S9, while the copy of byte 2 of the subblock is not changed for subsequent use.
- The byte found in S-box S9 in the previous step is XORed with the copy of byte 1 of the subblock as modified.
Then, the output of the f-function, the modified copy of bytes 1 and 2 of the subblock, is applied to bytes 3 and 4 of the subblock, modifying them permanently, as follows:
- The XOR of byte 3 of the block and the modified copy of byte 1 of the subblock are used to index into S-box S8. Byte 3 of the subblock is not altered by this step.
- The byte found in S-box S8 is XORed with byte 4 of the subblock, permanently modifying it.
- The XOR of byte 4 of the subblock as modified, and the modified copy of byte 2 of the subblock are used to index into S-box S8. Byte 4 of the subblock is not altered by this step.
- The byte found in S-box S8 in the preceding step is XORed with byte 3 of the subblock, permanently modifying it.

In the second round, bytes 3, 4, 1 and 2 serve the same functions as bytes 1, 2, 3, and 4 respectively did in the first round, and the four bytes of the second final output value perform the same function as the four bytes of the first final output value performed in the first round. The rounds are performed in place, so there is no interchange of bytes to move them into the positions of the bytes whose roles they now perform.

After each round, except the last, the four subblocks are to be interchanged as follows:

From the order:
1 2 3 4
to the order:
3 1 4 2

The Key Schedule

Quadibloc 2002 uses the following key material:

Seven 32-bit subkeys per round, K1 through K7 in the first round, K8 through K14 in the second round, and so on, for a total of 112 subkeys in all, K1 through K112, each 32 bits long, for a total of 448 bytes of subkey material.
Eight subkey pools per round, each containing sixteen 32-bit subkeys, SP1 through SP8 in the first round, SP9 through SP16 in the second round, and so on, for a total of 128 subkey pools in all, SP1 through SP128, containing a total of 2,048 subkeys, each 32 bits long, for a total of 8,192 bytes of subkey material.
Two key-dependent S-boxes, S10 and S11, each containing 256 sixteen-bit values, and composed of normal subkey material, for a total of 1,024 bytes of subkey material.
Two key-dependent S-boxes, S8 and S9, each containing one permutation of the bytes from 0 to 255.

The methods used to generate normal subkey materials and key-dependent permutations will be the same ones as developed for Quadibloc XI and subsequently applied as an option to several of the earlier ciphers in the series. Using them, first subkeys K1 through K112 will be generated, and then the contents of subkey pools SP1 through SP128. Then, S8 will be generated, followed by the contents of S10, and then S9, followed by the contents of S11.

The key will be a multiple of four bytes in length, and must be at least eight bytes in length.

Once again, the methods used to generate subkey bytes and key-dependent permutations are as follows:

Initialization

Three strings of bytes of different length are produced from the key.

The first string consists of the key, followed by one byte containing the one's complement of the XOR of all the bytes of the key.

The second string consists of the one's complements of the bytes of the key in reverse order, with three bytes appended containing the following three quantities:

The sum, modulo 255, of the bytes of the key, incremented by one by normal addition. (Thus, this produces a number from 1 to 255.)
The XOR of all the bytes at odd numbered positions in the key, where the first byte in the key is considered to be byte 1, and odd.
The one's complement of the XOR of all the bytes at even numbered positions in the key.

The third string consists of alternating bytes, taken from the bytes of the key in reverse order, and then from the bytes of the one's complement of the key, and then that string is followed by the one's complements of the first four bytes of the key.

Thus, if the key is:

 128  64  32  16   8   4   2   1   1   2   3   4   5   6   7   8

then the strings generated from it are as follows:

First string:
 128  64  32  16   8   4   2   1
   1   2   3   4   5   6   7   8
   8

Second string:
 247 248 249 250 251 252 253 254
 254 253 251 247 239 223 191 127
  37 170  93

Third string:
   8 127   7 191   6 223   5 239
   4 247   3 251   2 253   1 254
   1 254   2 253   4 252   8 251
  16 250  32 249  64 248 128 247
 127 191 223 239

Given that the length of the key is 4n, the lengths of the three strings are 4n+1, 4n+3, and 8n+4, and hence all three are relatively prime, since both 4n+1 and 4n+3 are odd, and 8n+4 is two times 4n+2.

Two buffers, each containing room for 256 bytes, are filled by generating bytes from the first and second strings by placing them in a nonlinear shift register.

The form of that shift register is shown in the following illustration, showing its precise form for the first string.

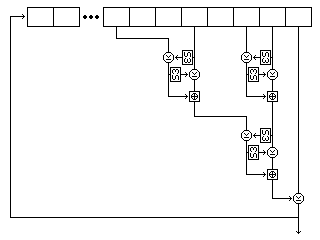
Five bytes are read from the string at each step. For the first string, they are, as shown in the diagram, the eighth-last, fifth-last, third-last, and second-last bytes and the last byte. For the second string, they are the eighth-last, seventh-last, fourth-last, and second-last bytes, and the last byte. For the third string, they are the twelfth-last, tenth-last, seventh-last, and fourth-last bytes, and the last byte.

Each time the shift register produces a byte, it does so as follows:

The second byte read is used to select an entry in S-box S3, and the value of this entry is XORed to the first byte. Then the first byte is used to select an entry in S-box S3, and the value of this entry is XORed to the second byte.
The fourth byte read is used to select an entry in S-box S3, and the value of this entry is XORed to the third byte. Then the third byte is used to select an entry in S-box S3, and the value of this entry is XORed to the fourth byte.
The first and second bytes, as modified, are added together using modulo-256 addition to form a first result.
The third and fourth bytes, as modified, are added together using modulo 256 addition to form a second result.
The second result is used to select an entry in S-box S3, and the value of this entry is XORed to the first result. Then the first result is used to select an entry in S-box S3, and the value of this entry is XORed to the second result.
The two results as modified are added together using modulo 256 addition to form a third result.
The fifth byte read, which is always the last byte in the shift register, is XORed with the third result. The resulting value is output as the byte produced by operating the shift register.
The values in the shift register are modified by removing the last byte, advancing the bytes in the shift register to the next later position, and appending the output result as the new first byte of the shift register contents.

Both buffers contain 256 bytes. The first buffer, called buffer A, is filled with 256 successive bytes generated from the second string by means of the nonlinear shift register filled with the second string. The second buffer, called buffer B, is filled with 256 successive bytes generated from the first string by means of the nonlinear shift register filled with the first string.

Subkey Byte Generation

Once the setup is complete, subkey material is generated one byte at a time, the first byte generated being the leftmost byte of subkey K1, and so on.

A subkey byte is generated as follows:

A byte is generated from the first string by the nonlinear shift register operation.
The byte at the position in buffer A indicated by this value is taken, and called P.
A byte is generated from the third string by the nonlinear shift register operation. In the case of the third string, the shift register operation involves reading the following five bytes: the twelfth, tenth, seventh, and fourth last bytes, and the last byte. The value of the byte thus produced is placed in buffer A, replacing the value taken.
A byte is generated from the second string by the nonlinear shift register operation.
The byte at the position in buffer B indicated by this value is taken, and called Q.
A byte is generated from the third string by the nonlinear shift register operation. Its value is placed in buffer B, replacing the value taken.
The subkey byte generated is the XOR of P and Q and an additional byte generated from the third string by the nonlinear shift register operation. (The use of an additional byte from the third string ensures that all the bytes of the key particpate directly in the key schedule; otherwise, some could be skipped over in a sense by the selection of bytes to use from the buffers.)

The following diagram attempts to illustrate the complete process of subkey byte generation:

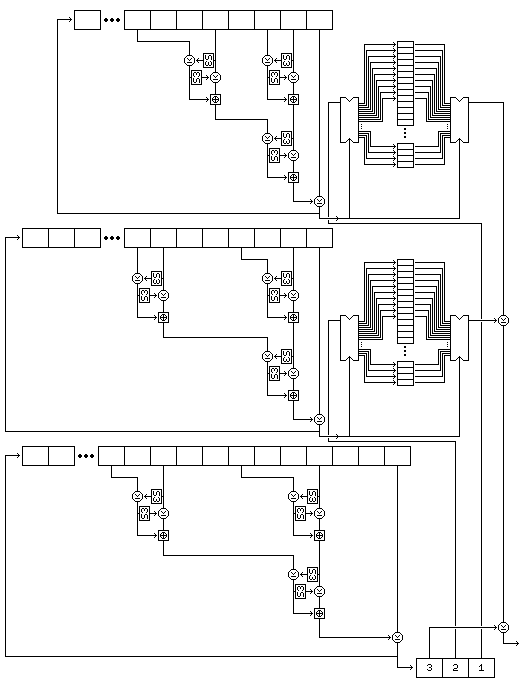
Note that this procedure, since it exercises the two strings used to select bytes, rather than the string used to generate values, results in a small change in the key resulting in large changes in the subkeys from the very beginning.

Permutation Generation

Once all the required 32-bit subkey words are generated, the key-dependent S-boxes S8 and S9 must be generated. To generate each bijective S-box, the following procedure is used:

256 bytes are generated following the same procedure as for subkey byte generation, and these bytes are placed in a 256-byte buffer called buffer C.
A 256-byte buffer called buffer D is filled with the numbers from 0 to 255 in order.
For every i from 0 to 255, if element i of buffer C (hereinafter called C(i)) is not equal to i, swap elements i and C(i) of buffer D.
For every i from 0 to 255, if B(i) is not equal to i, swap elements i and B(i) of buffer D.
For every i from 0 to 255, if A(i) is not equal to i, swap elements i and A(i) of buffer D.

The resulting contents of buffer D are used as the key-dependent bijective S-box intended to be produced. Note that this is a procedure, introduced for Quadibloc X, is more straightforwards than the other two basic procedures used previously to produce S8 in other ciphers in this series.

This procedure, although it uses buffers A and B, leaves them undisturbed; thus, byte generation may continue after one S-box is produced.

Long Keys

The subkey generation procedure given above works well for keys from 64 bits to 1,024 bits in length. When the length of the key approaches 2,048 bits in length, however, the first two shift registers are no longer thoroughly mixed by filling the buffers initially.

Thus, the following modified subkey generation procedure is given for keys which are more than 1,024 bits long. A key must still be a multiple of 32 bits in length.

(1) Divide the key into blocks of 512 bits until the remaining part of the key is from 512 to 992 bits in length.
(2) Use the first block of the key as the key for the normal Quadibloc 2002 key schedule.
(3) Continue to generate enough additional subkey bytes to XOR these with the next block into which the key was divided.
(4) Use the next block, after the XOR, to carry out the Quadibloc 2002 key schedule except:
- The subkey material generated is XORed with the previously generated values of the subkeys;
- When using the second block, the first four bytes of subkey material generated are XORed with K2 instead of K1; after S11 is filled, then go back and generate four bytes of subkey material to XOR with K1. For each succeeding block, start 32 bits later in the key schedule, until one has used one block to modify the subkey material beginning with the last (sixteenth) subkey in subkey pool 56; then, with the next block, begin again from K1. (This ensures that S8 and S9 are always generated relatively late in the sequence.)
- Generate permutations for S8 and S9 in the normal sequence of generation, and then modify the S8 and S9 to be used in the cipher as follows: go through the newly-generated S8 or S9 and the previously calculated S8 or S9 from positions 0 to 255; in a new array, place the value in the new permutation in the position indicated by the value in the original permutation. Once this is finished, the new array is the replacement permutation.
(5) If there are any additional blocks remaining in the key, go back to step 3.

This method ensures that the key schedule is a function of the entire key.

Variations

The first variant of the cipher defined is Quadibloc 2002 ED (Enhanced Diffusion). In this variant, the round is modified by performing the following additional operations:

Prior to being used as an input to the f-function computation, the second subblock is modified by being XORed with the XOR of the first intermediate value of the first subblock and the third intermediate value of the first subblock.

Subsequent to being used as an input to the f-function computation, the third subblock is modified by being XORed with the XOR of the second intermediate value of the first subblock and the fourth intermediate value of the first subblock.

This, at a cost of four 32-bit XOR operations, considerably increases the speed of diffusion in the cipher, as the two subblocks which originally were not changed by a round are now both modified based on the contents of the first subblock. Although the intermediate values of the first subblock are somewhat more exposed by this change by being used in this manner in addition to being used deep within the involved f-function computation, the fact that they are only used this way when XORed in pairs reduces the problem.

Although 16 rounds are still recommended, if it is desired to use the cipher with only 8 rounds, the ED variant should be used.

A second variant of this cipher, Quadibloc 2002 BT (Byte Transpose) attempts, without defining a special round type, to achieve what is achieved by the mixing and whitening phases of Quadibloc VI and VIII, as well as the special rounds at the beginning and end of Quadibloc II and III.

In Quadibloc 2002 BT, after rounds 4, 8, and 12, instead of transposing the four subblocks in the "tire rotation" pattern normally used, the sixteen bytes of the block are transposed from the order

 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16

to the order

 1  5  9 13  2  6 10 14  3  7 11 15  4  8 12 16

Note that this byte transposition is its own inverse. In this way, because the parts of a subblock are thoroughly combined by the outer rounds, the role any bit will be in within the inner rounds is assumed to be obscured by this.

In addition, rounds 1 through 4, and rounds 13 through 16 are of the ED type, while rounds 5 through 12 are normal.

The byte transpose also speeds diffusion, because now even the transformations of the first subblock by itself serve to encipher the block as a unified whole. Think of Square, the predecessor of Rijndael, but with only four rounds (but without the special type of round that allows a specific saturation attack against it). However, since the byte transpose doesn't include the "tire-rotation" transpose of the subblocks as an implicit part, when it is reversed, the phase of the subblock arrangement is changed, and this may seem to be a weakness.

With only eight rounds, a byte transposition in the middle would not strengthen the cipher appreciably, due to the boomerang attack, and in that case making the succession of rounds unbalanced for some bytes, it may even weaken the cipher. But for sixteen rounds, it should strengthen it, and strengthen it appreciably, particularly in terms of its strength under severe weak key conditions.

Why Not Four Rounds?

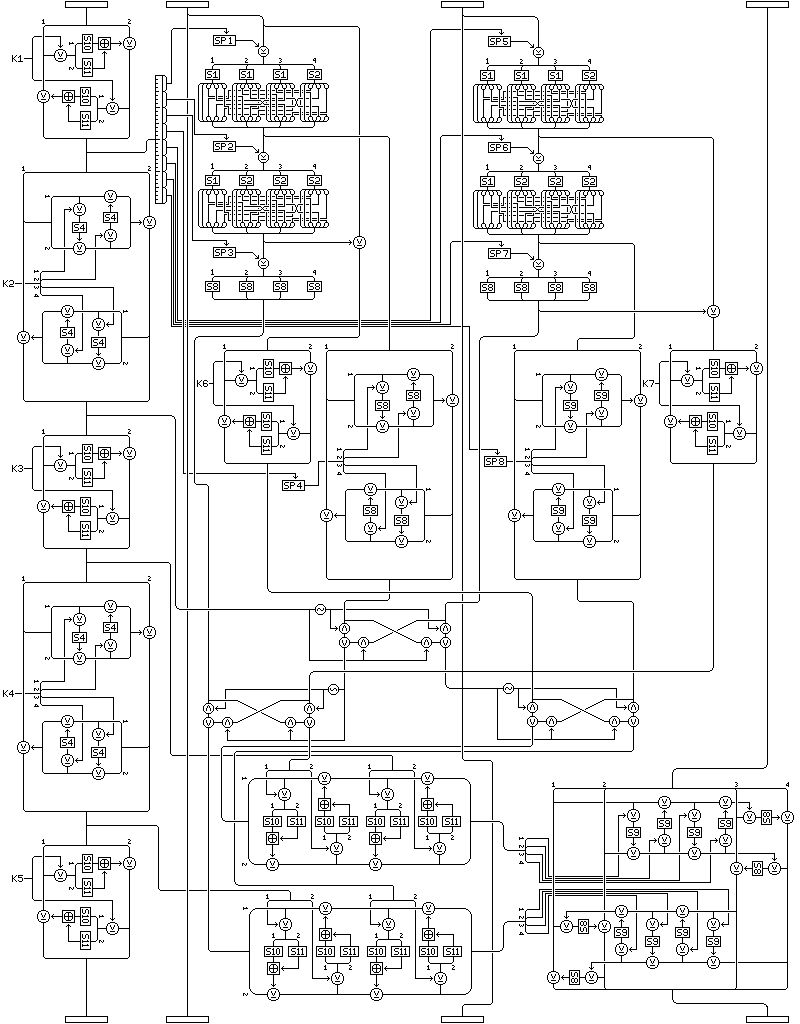
The Quadibloc 2002 round is large and elaborate. Yet, it is proposed that this cipher have 16 rounds, the same number as was used by DES, with its much simpler round structure. Why can't one take advantage of this complexity to still have a secure cipher with only four rounds?

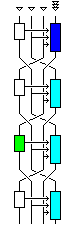
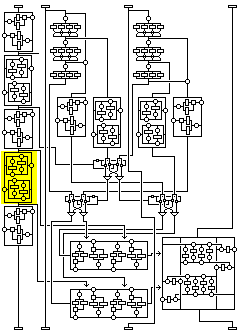
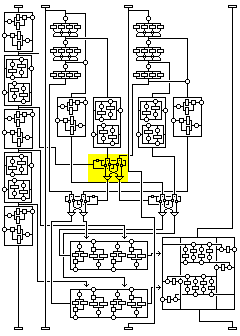
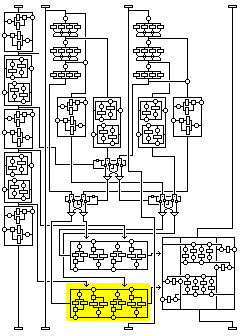
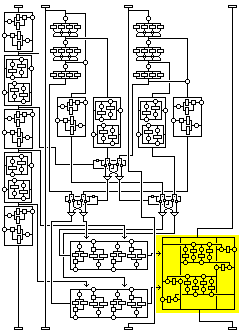
The diagram at right gives a high-level overview of the cipher. And it shows what can happen in the case of a certain kind of chosen-plaintext attack.

Each round is shown here very simply; the first subblock is subjected to a transformation that depends on itself alone (and, of course, the key) and the fourth subblock is subjected to a transformation that depends on all three other subblocks.

If one keeps the first three subblocks constant, in a series of plaintext blocks varying only in the fourth subblock, then the transformation depending on the other subblocks which takes place in the first round, shown in blue, never changes. And the only other time this subblock will change is in the transformation which is independent of the other subblocks, shown in green, that takes place in the third round.

The complicated transformations that the other subblocks undergo, shown in light blue-green, are not a problem. However the other subblocks may change differently because the fourth subblock changed on input, the output subblock corresponding to the fourth subblock, which is the second subblock, will run through all possible values, without duplicates, if one runs through all the values of the fourth subblock on input while holding the other three constant.

If it were not for the fact that the first subblock is changed as a unit in a complicated way, it would not be necessary to mount a saturation attack with 2^32 chosen plaintexts to observe this, since if you look at the combiner operating on the fourth subblock in detail, its fourth byte is the first one modified by the XOR of a value obtained from the three other bytes. Thus, changing that fourth byte by a pattern of bits, while it results in the rest of the subblock changing in a complicated way, and then other subblocks changing in a complicated way in later rounds, has the immediate result of changing that fourth byte in the output by that pattern of bits. (Of course, this "weakness" applies to the entire half of the block being modified in a classical Feistel round cipher.) But because the first subblock does also change, this simpler distinguisher works only after two rounds.

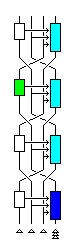
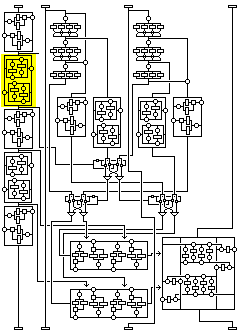
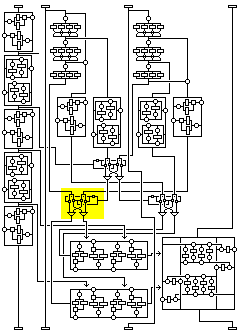
The same thing can be done for the fourth subblock of ciphertext blocks in a chosen-ciphertext attack.

The only time that subblock is changed in a way that depends on the other subblocks is in the fourth round. So if ciphertext blocks are changed only in the fourth subblock, as it is deciphered, it is subjected to the same two transformations; the one in the fourth round that is the same because the other subblocks are constant, and the one in the second round that is independent of the other subblocks.

Thus, the plaintext block output which corresponds to it, the third subblock, is in this case connected to the fourth subblock by a substitution.

What about the other two blocks? The situation is not so simple in their case.

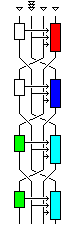
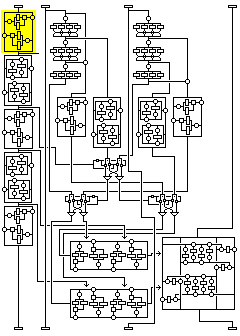
Let us say that one wants to mount a chosen plaintext attack where the second subblock is varied. In this case, the substitution depending on the other three subblocks takes place in the second round, where the second subblock becomes the fourth.

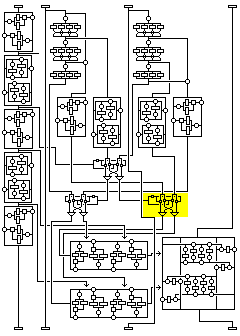
Holding the third and first subblocks constant in the plaintext ensures that the first and second subblocks remain the same in the second round.

But because the second subblock has changed, the fourth subblock, transformed in the first round in a way that depends on the second subblock, in the box shown in red in the diagram, will, as the third subblock in the second round, be different.

However, it is possible to identify its distinct values, since the output from that transformation, which is what we would like to keep constant, only goes through one other transformation, the one in the third round that is independent of the other subblocks.

So, for each input value of the second subblock, we can try to find the value for the fourth subblock that produces a desired constant value of the second subblock on output. For these values, the transformation of the second subblock on input to the first subblock on output will be a substitution.

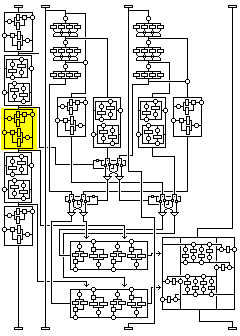
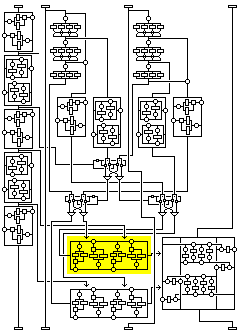
Thus, substitutions for two of the subblocks can be obtained for a particular case in 2^32 tries, and for the other two in 2^64 tries. By themselves, of course, these substitutions won't allow one to decipher any part of blocks corresponding to other cases.

Not shown in the small overview diagram is the fact that there are only 2^64 possible transformations of the fourth subblock in a round; although it depends on the three other subblocks, two 32-bit values are derived from them which alone control how the fourth subblock is modified. This bottleneck also may simplify the process of searching for structure in this cipher for a given key.

None of this makes it easy to read plaintext, even for the four-round version of this cipher; but the fact that there is any visible structure at all, instead of a substitution that is completely opaque, against which nothing can be done short of recording the output for all 2^128 possible inputs, means that the four round version cannot be considered to be completely devoid of weaknesses.

Next
Start of Section
Skip to Next Chapter
Skip to Next Section
Table of Contents
Main Page