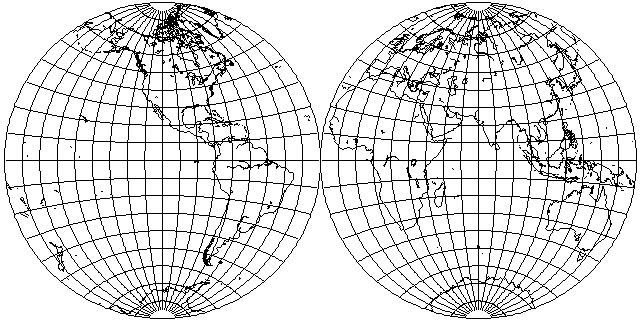
This is a projection that at one time was quite popular in atlases.

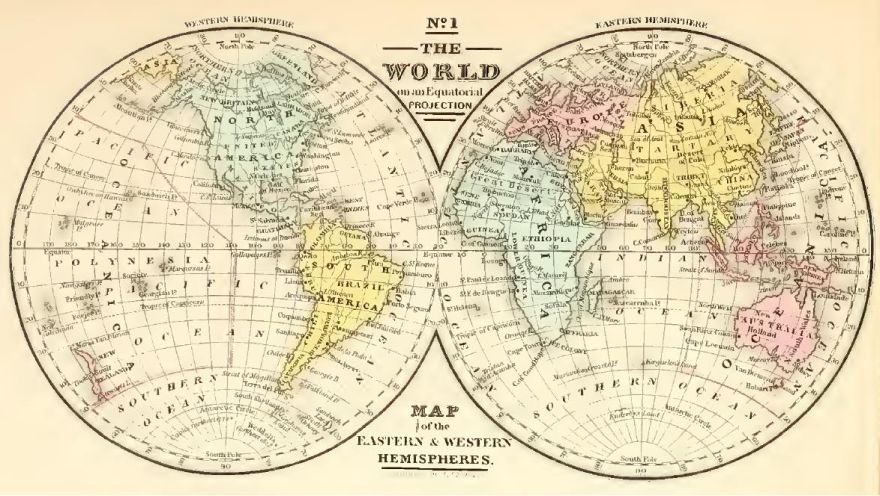
And here is an example of its use in one old atlas:
It is a projection that is very simple to construct with compasses and straightedge, and which approximates the characteristics of the equatorial case of the azimuthal equidistant projection. Thus, when a hemisphere in which a compromise between conformal and equal-area characteristics is desired is to be drawn, it was a natural choice. Today, with computers to do our work for us, projections designed for ease of manual drawing have, though, become less popular.
This projection was devised by Giovanni Battista Nicolosi in 1660, and was a clear improvement on earlier attempts at a conventional projection of a hemisphere by Bacon, Apian, and Fournier. However, this was an independent re-invention of the projection; it had first been described by al-Biruni in one of his works, in which the Azimuthal Equidistant projection is also described, as well as six other map projections, from about the year 995 or 1005.
Some sources, however, appear to state that the projection we are familiar with as the globular projection was not, in fact, re-invented in exactly the form usually used by Nicolosi, but instead a slight revision of what he had invented by Phillipe de la Hire is what produced the same projection as previously devised by al-Biruni. This is surprising, as the difference between this projection and the previous one devised by Georges Fournier (in which the parallels were drawn the same way, but the meridians were ellipses passing through the Equator at equal intervals) is already slight.
As de la Hire did devise a perspective azimuthal projection which also approximated the Azimuthal Equidistant projection for a hemisphere, it is possible that this is what led to confusion.
The construction is simple enough. The equator is divided uniformly into points corresponding to the different longitudes, and the meridians are circular arcs drawn between these points and the poles. The bounding circle and the central meridian of the hemisphere are divided uniformly into points corresponding to the different latitudes, and the parallels are circular arcs joining those points.
While the projection is intended to make a nice-looking hemisphere, simple to construct, but almost as good as an Azimuthal Equidistant, the way in which it is constructed doesn't restrict it to a hemisphere; it could be continued to show the whole world:
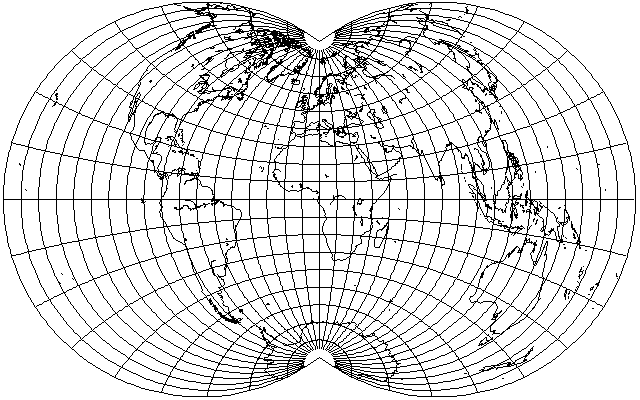
Although it's not particularly attractive as a whole-world projection, this might be useful for extending a hemisphere by a small amount to show a piece of a continent that is cut off.
What if, instead of dividing the border of the hemisphere equally, to make a better projection of the whole world, divide the border of the whole-world map equally?
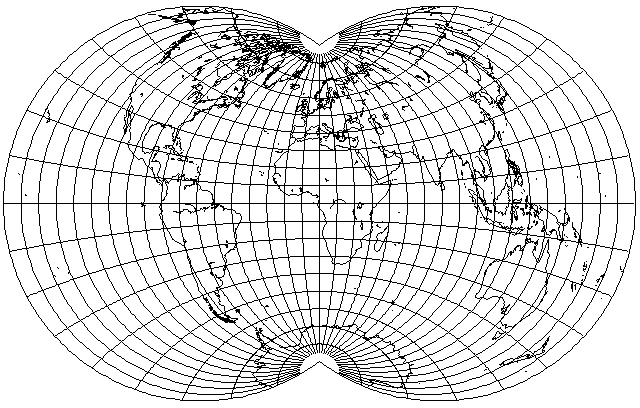
In 1888, Henri Bouthillier de Beaumont, of Geneva, obtained U. S. Patent 400,642 for the map projection that resulted when he asked himself that question, and, indeed, this is an improvement.
The image below is from an atlas with the title "Atlas Designed to Illustrate the Malte-Brun School Geography", from 1834. The author is one S. Griswold Goodrich; it is published by F. J. Huntington, to which the maps are credited.
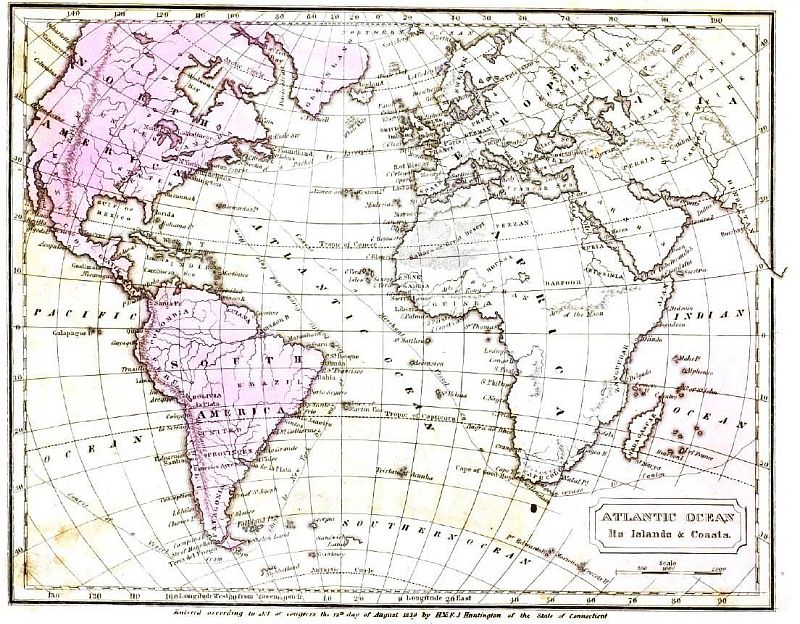
Conrad Malte-Brun was a famous French geographer, and his Precis of Universal Geography appears to have been for a time the standard work on world geography.
This map came to my attention when I saw an image of a map with a somewhat similar appearance in a discussion forum; I looked for more information, and first found images of this map as one offered for sale, and then I found the old atlas from which it came.
Although it looks reminiscent of the Nicolosi Globular projection, I had been informed by the post where I saw what appears to be another example of the same projection, that it wasn't, so I took a closer look and confirmed that.
The following illustration
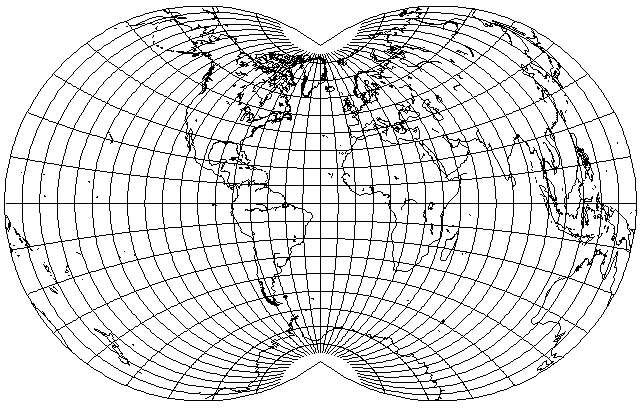
shows an attempt on my part to approximate what the projection of that map might be.
It is constructed almost as the Nicolosi Globular projection is constructed, except that the points on the boundary of a circular hemisphere through which the arcs for the parallels of longitude pass are moved one-quarter of the way, along that circular boundary, from their positions equally spaced in angle from the Nicolosi Globular to positions equally spaced in height from the equator (with the position of the poles remaining constant).
I had first moved the boundary points halfway instead of one-quarter of the way, and as comparing the map to both the Nicolosi Globular and to that guess made it appear that the map's parallels were halfway between the two I came to the conclusion that a three-quarters/one-quarter mix was used.
This is a very simple and straightforward way to modify the Nicolosi Globular projection to render it suitable for depicting areas of a greater extent in longitude.
Incidentally, the shape that is shared by the world-wide form of the Globular projection, the Henri Bouthillier de Beaumont projection, the projection above, and the Van der Grinten IV projection which we will meet shortly, can be worked out,
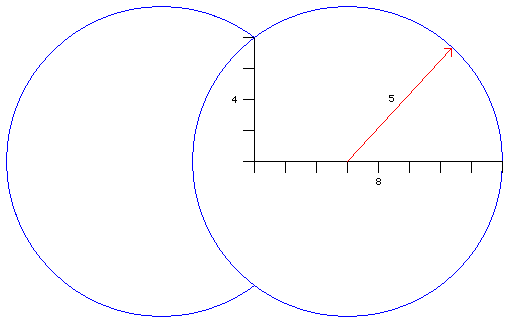
and it turns out to involve the ancient 3-4-5 Pythagorean triangle. So the projections belonging to this family are 1 3/5 times as wide as they are high.
A modification of this projection is referred to in The Study of Map Projections by Steers, apparently invented by the cartographer A. M. Nell (also known from the Nell-Hammer projection, which was inspired by another of his projections, but devised by Hammer). In this, the central meridian and Equator have scales placed on them which are the arithmetic mean of the uniform ones of the globular projection and those of the Stereographic, in which the parallels ane meridians are legitimately circles.
One can view the Globular projection as an attempt to approximate the equatorial case of the Azimuthal Equidistant. Since Airy's minimum-error azimuthal involves a limited expansion of radial scale away from the center, one could also, but it would be rather more of a stretch, view this projection as an approximation to Airy's projection!
Of course, for a closer approximation to something with minimum error, one could take the scale on the central meridian and the Equator from Clarke's minimum-error perspective projection, and still have something very easy to construct!
Speaking of evil shortcuts... a 1943 paper by Richard Edes Harrison, The Nomograph as an Instrument in Map-Making cited in Edwin Raisz' book General Cartography and elsewhere, showed how the graticule of the equatorial case of an azimuthal projection could be used as a tool to draw the same projection in any oblique case.
I tried to illustrate it here, but I'm not sure I really succeeded.
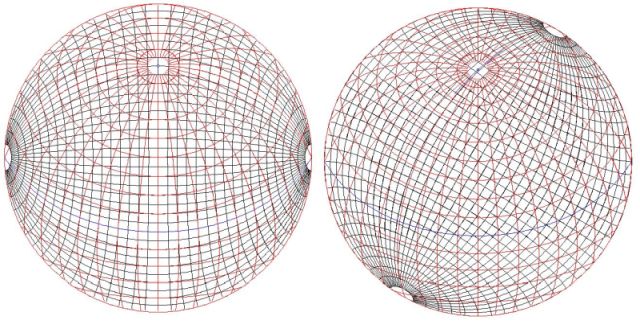
The nomograph bearing the equatorial graticule is shown in black, and the desired oblique aspect is shown in red.
The first step is shown on the left. With the nomograph turned sideways, pick a meridian corresponding to where you want to put the equator, copy that, and also the points where parallels cross that meridian will be the points where meridians cross the equator on the projection, so mark them off. As well, where the meridian on the nomograph 90 degrees away from the one you've used for the equator is located, where it crosses the equator on the nomograph is where to mark the North Pole (or the South Pole, depending on what you're drawing) on the map you're making.
The right half shows how to draw one meridian on the map. Tilt the nomograph so that one meridian on it (of course, the actual meridian you need may be between two meridians on the nomograph) intersects both the point marked on the equator for that meridian's longitude and also the pole on the map you're drawing. That is what you need to trace to draw that meridian.
The globular projection, of course, is not an azimuthal projection, but it resembles the equatorial case of one. What if someone were to use it with this same technique?
No, the results wouldn't be a mess. As the projection being drawn got more and more oblique, the resulting projection would be less and less like the globular, and more and more like the Azimuthal Equidistant, and so rather than it getting worse, the globular projection would be improved if obliqued in this way rather than by a genuine coordinate transformation.
Of course, this means that every map with a different degree of obliquity would be on a different projection.
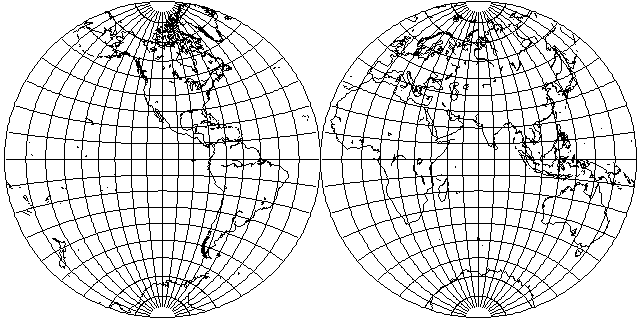
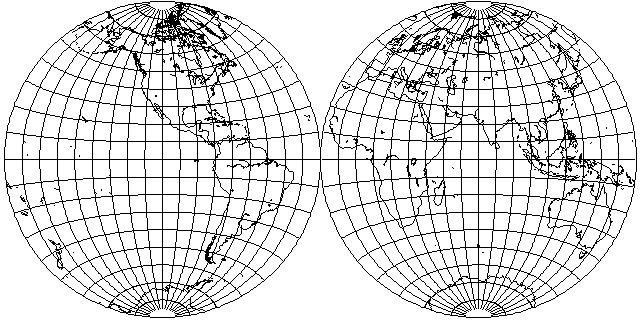
As noted, because the Equator and the central meridian are divided equally in the Nicolosi Globular projection,

it closely resembles the Azimuthal Equidistant projection, at least for hemispheres:
On my page about Bonne's Projection, I discuss such projections as Bartholomew's Tetrahedral projection. As it happens, a map with four lobes proceeding from the Northern Hemisphere was produced by Johann Conrad Hinrichs as far back as 1811.
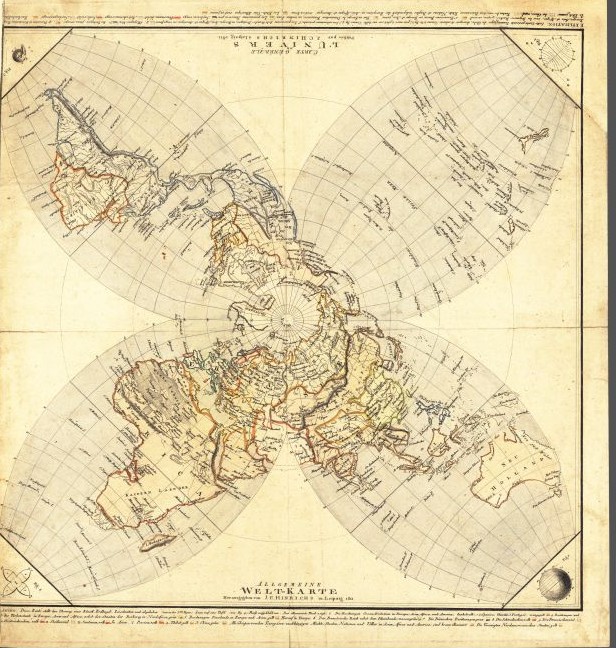
But this map apparently uses the principle of the Globular projection as the basis for those lobes, with 37 degrees North latitude apparently being the boundary between them and the polar azimuthal projection in the center.