Under this heading are classed projections designed to be relatively easy to draw with the aid of drafting tools, but which do not correspond to any of the regular types.
These projections are compromise projections, although different ones choose to strike different balances between the rival goals of being conformal and being equal-area. Thus, the Globular projection is about midway between these two options, while the Van der Grinten projection moves only slightly in the direction of reducing area distortion at the cost of shape distortion.
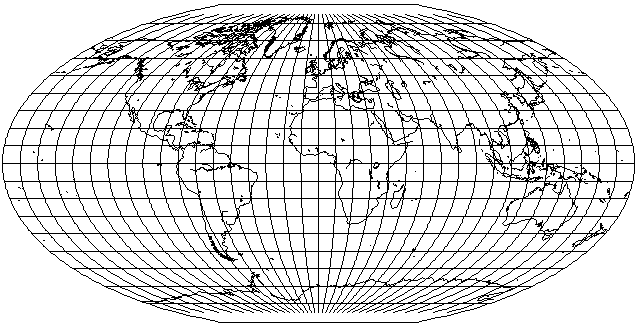
I'm not sure whether the Denoyer Semi-Elliptical Projection should be classed among the pseudocylindrical projections (its parallels are horizontal lines) or the conventional projections (longitude spacing along the parallels is unequal).
Existing mapping programs attempt to replicate it, but their attempts have some of the inner meridians touching when they reach the pole lines, like the Ortelius Oval; the actual Denoyer Semi-Elliptical had the scale decrease quite a bit along the pole lines near the central meridian, but to about an eighth or so of what it was on the edges, not to zero. This is why I thought I would make an attempt:

At the edges, the curve of a meridian is an ellipse with a width of 360 degrees and a height of 190 degrees - a 5 degree excess at the top and bottom, yielding pole lines.
Two other parameters I have left as adjustable, for this attempt, I have set as follows: at the limit at the central meridian, the curve of a meridian is to intersect the central meridian 3 degrees outside the poles at the top and bottom: making this smaller is what allows the meridians to be bunched closer together near the poles. The shape the meridian belongs to, however, will be an ellipse which in height extends 30 degrees above and below the pole lines; this figure was chosen arbitrarily; this is so that, as in the real Denoyer Semi-Elliptical projection, the meridians near the center don't start turning inwards rapidly near the poles, like those of the Mollweide, but instead look more like circular arcs.
Built into the code for the projection, again, to make it resemble what I had seen to be the appearance of the Denoyer Semi-Elliptical projection, the proportion by which any given meridian embodies the characteristics of the border (which has a curve height and an interception location that are the same) and of the limit at the central meridian is calculated as follows:
Let x equal the longitude divided by 180 degrees. The first proportion is x squared. Take one minus the first proportion, and cube it. The result is the proportion to which the central meridian attributes are used, one minus that result is the proportion to which the border attributes are used.
No doubt some simpler, more geometric scheme was actually used by the real Denoyer Semi-Elliptical Projection, but this at least seems to approximate it.
Also, here is an image of the Butterfly projection of B. J. S. Cahill:
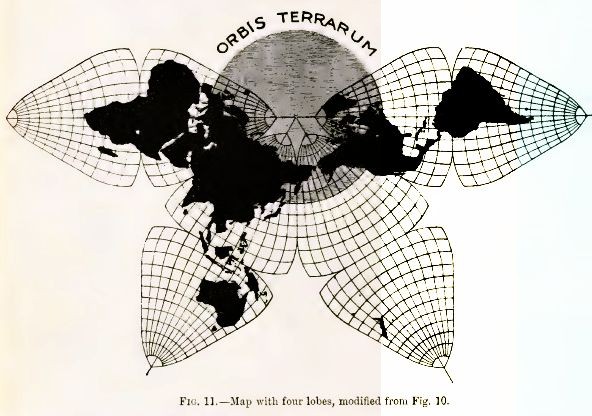
One that I've found that I am able to reproduce, although I was somewhat unhappy with the quality of the original, doing the best I can to enhance it, I think I have achieved something passable.
I have found a better one that I may use, shown below:
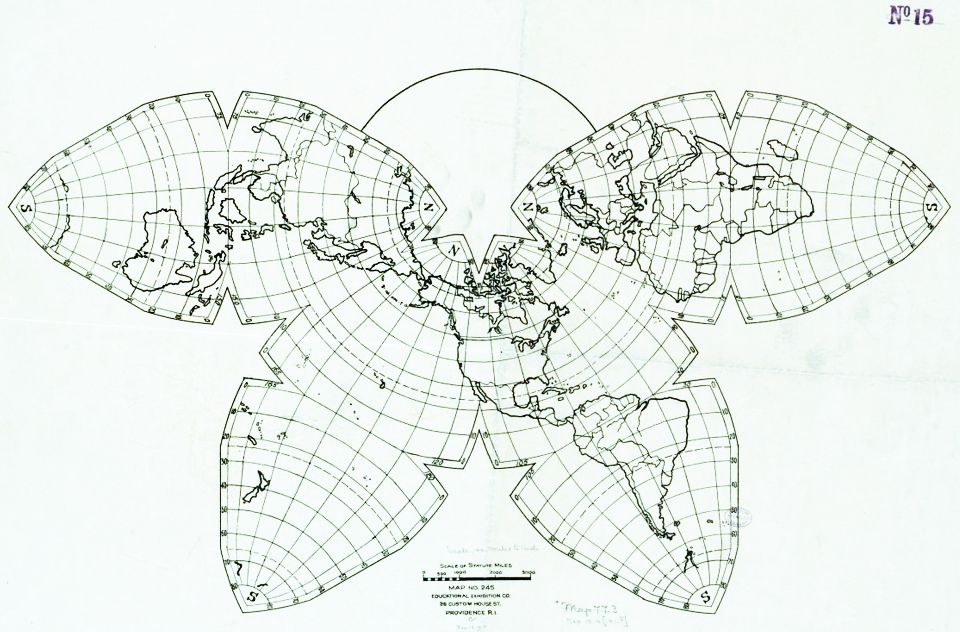
Map reproduction courtesy of the Norman B. Leventhal Map & Education Center at the Boston Public Library
I have performed some image-editing operations on the image above to improve its contrast, and so this is not an exact reproduction of the original.