The polyconic projection, as shown here,

is not particularly suitable to a map of the world.
However, if one scales latitude and longitude both down to one-half their value, one obtains a map like the following:
which looks somewhat more promising.
In the polyconic projection, there are actually a number of different parameters that can be scaled independently. For example, let us begin by only changing one thing: let the radius of the arcs used for the parallels be determined by a latitude one-ninth of the actual latitude:
Because the parallels don't have the correct radii, I class this projection as a conventional projection, even though it is based on the Polyconic projection.
The result, with true scale along the parallels, resembles the sinusoidal, but the curved parallels do mean that it is not equal-area. Now, let us reduce shear by using a latitude that is 3/4ths of the actual latitude to determine the scale of longitude along the parallels:
At this point, we have quite an attractive-looking projection. It is most accurate at the equator, however, with stretch even at temperate latitudes.
Let us shift the intersections of the arcs for the parallels with the central meridian by stretching them, without otherwise stretching the projection, so that those arcs remain circles, by a factor of 1.218188, which will make 48.75 degrees latitude the standard parallel of the projection:
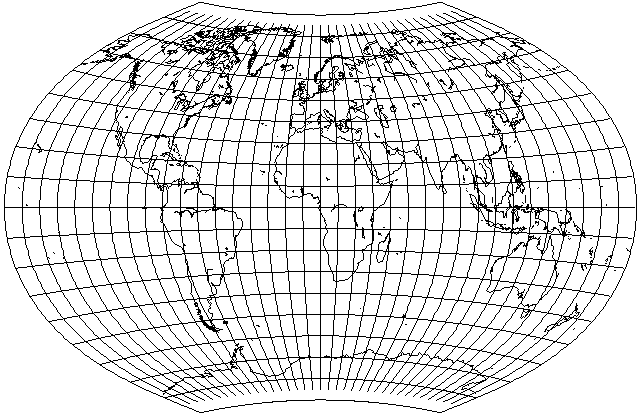
Finally, let's make our standard meridian 32.5 degrees East longitude the standard meridian, but have the projection asymmetrically disposed around the standard meridian, being primarily divided at 120 degrees west longitude, but allowed to extend beyond that range:
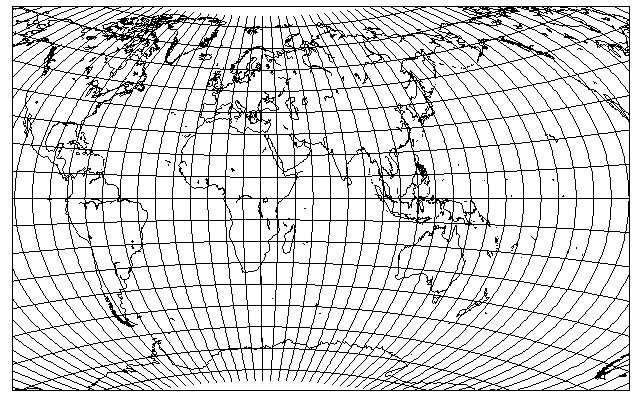
and one obtains an attempt at an approximation to the map projection often seen for maps of the world in Soviet atlases, as devised by one G. A. Ginzburg. This is the Ginzburg VI projection, he has also devised several other projections of different types.
Here, in greatly reduced size, is an actual example from a Soviet atlas of the use of this projection:
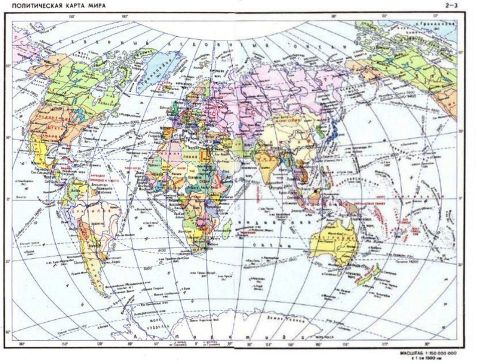
I felt the reduction necessary because of quality degradation in the image due to the steps needed to stitch the two halves of this map, originally on two separate pages, together.
Here is what this projection looks like when rendered by G-Projector:
Let us again let the radius of the arcs used for the parallels be determined by one-ninth of the latitude, but this time, let us have the scale along them be determined by two-thirds (rather than three-quarters) of the latitude. Also, a similar, but rounded-off vertical stretch of one and two ninths, is applied. The result, with 150 degrees East longitude as the standard meridian, is:
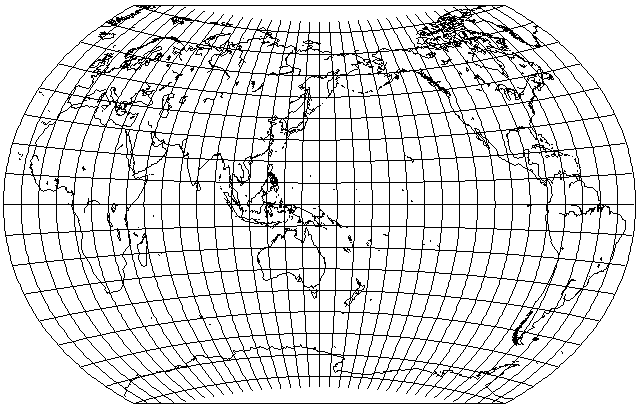
which resembles some maps from the People's Republic of China. Could this be the lost recipe for the Latitudinally Equal Differential Polyconic Projection? However, while it closely matched one older Chinese map having the same general appearance, newer ones with that same general appearance seem to have the spacing of the parallels increasing somewhat as they approach the poles, rather than it being uniform, as here.
Here is this projection as rendered by Justin Kunimune's Map Designer:
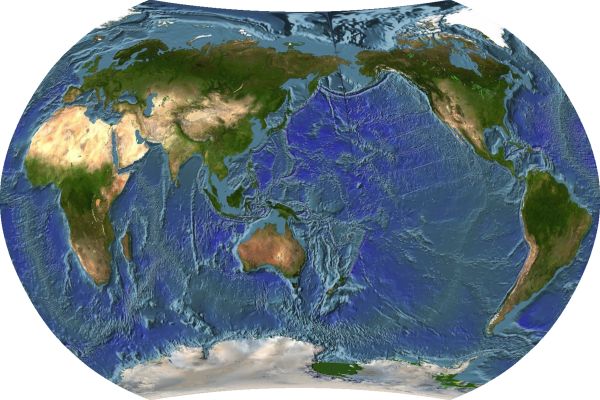
The projection has been more recently been employed in this transverse aspect:
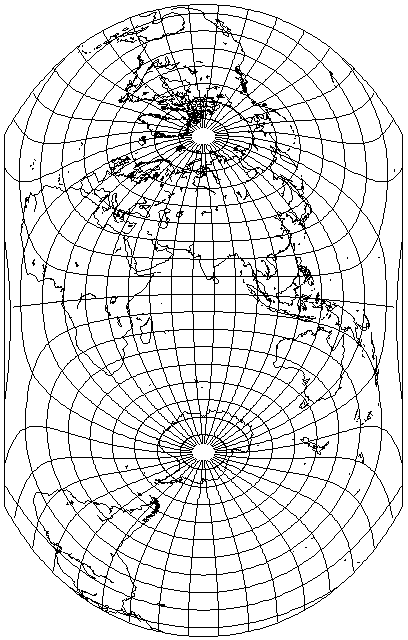
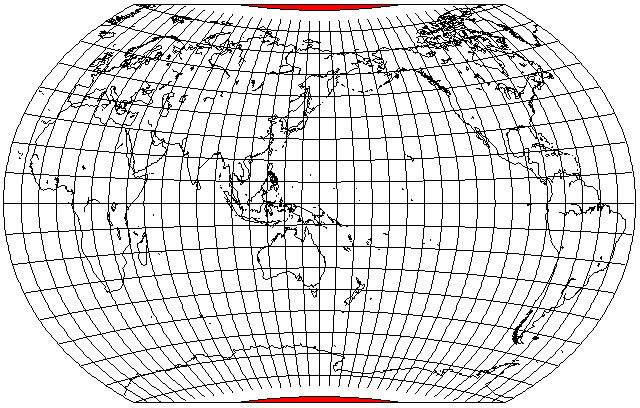
Incidentally, this aspect makes visible the fact that the projection, as usually drawn, shows part of a pole line - but the area beyond the pole line just has the blue color of the ocean (or the white color of Antarctica) continued into it, thus obscuring the fact that some points within the projection don't actually correspond to real points on the globe. This map shows those areas marked in red:
And it was also used in this transverse aspect
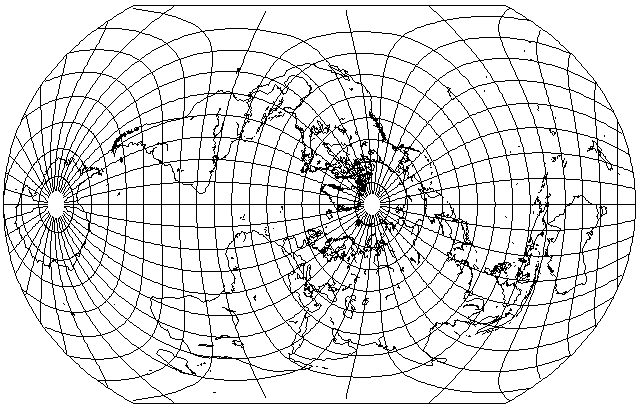
for a news article illustrating the exciting prospect of shorter maritime trade routes from China to Europe and to the Eastern Seaboard of the United States should the North-West Passage become open.
Not only does this aspect resemble Bartholomew's Atlantis projection, but in fact this projection happens to have its lowest angular distortion around the points which, in the conventional aspect, correspond to 30 degrees north and south on the central meridian, so it could actually be usefully employed in the same aspect that John Ian Bartholomew used.
It is only recently that this particular map projection has come into very common use in China, so much so that it almost seems that other world map projections are not used at all. That, though, is unlikely to be the case. In looking for earlier maps from the Chinese mainland, I found one example of a present-day map with an antiqued style, not unlike some National Geographic Society products, which was in a Winkel Tripel projection with a 150 degree central meridian:
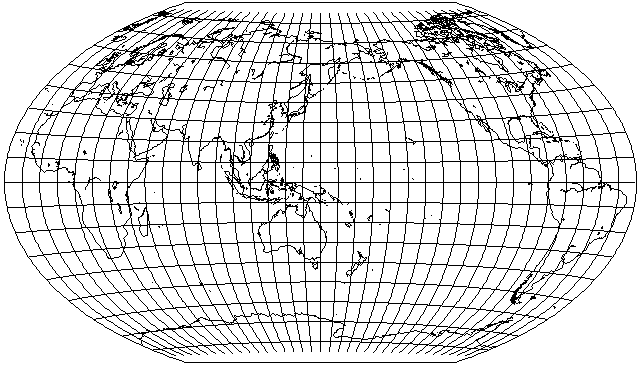
and this resembled something I had encountered in an earlier search: I couldn't find images of the maps of the world used by schoolchilren in North Korea, but a decorative world map on a wall happened to have somewhat of a resemblance to this.
More recently, I made another web search, and I found an actual North Korean world map on Reddit; it turned out to be made with the same map projection as discussed above as being popular in mainland China.
One important point should be addressed before going forward.
It is possible that a naïve reader of this page might look at my illustration of the Ginzburg projection, as used in the Soviet Union, with its center shifted eastwards from the Greenwich meridian towards Moscow, or of maps as used in the People's Republic of China, where the edge of the map is placed in the Atlantic Ocean instead of the Pacific, and conclude from them that this indicates an excessive, and perhaps even insanely paranoid, level of nationalism present in those countries.
This would be to use an unsound basis to draw that conclusion. It is entirely natural that a map of the world should present to its intended viewers accurate information on how the rest of the world is related to them.
Thus, in the democratic and peaceful United States of America, the National Geographic Society has, in the past, published maps that look like this:
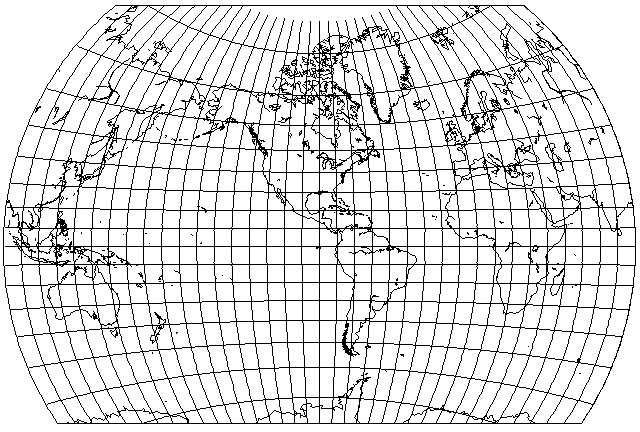
this map being one on the Van der Grinten projection, with its central meridian at 90 degrees West longitude, so as to show the areas closest to the United States in a westward direction on its west, and those closest to it in an eastward direction on its east.
As another example, in Japan, the Mercator projection may be used for a map like the following:
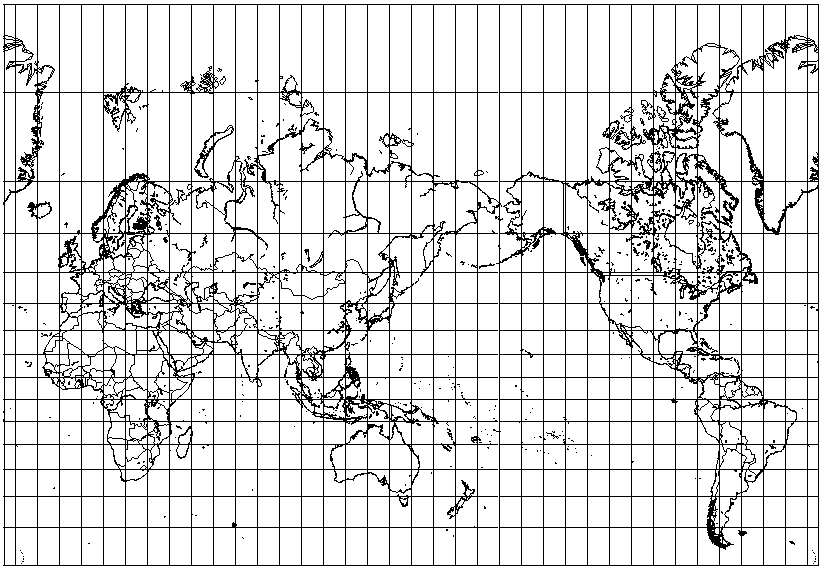
and, again, this only makes sense, given their country's point of view.
Of course, other combinations of parameters are possible. For example, if I allow the parallels to have more curvature, by scaling the latitude to 1/4th of its value for that purpose, and I also choose a shorter pole-line, by using 8/9ths of the latitude to determine the longitude scale along the parallels, I obtain the following:
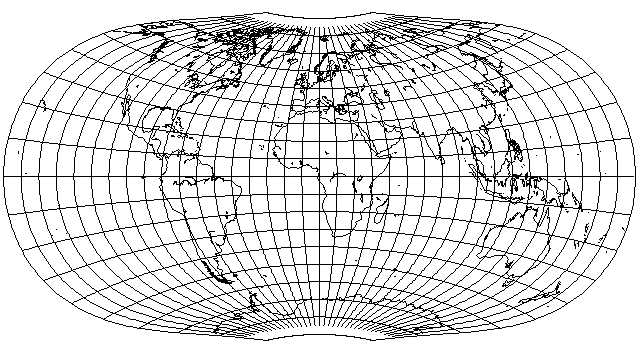
This is interesting, but the pole-line is perhaps a bit too small. However, it is interesting to note that this projection does have a slight general resemblance to the Laskowski Tri-Optimal projection:
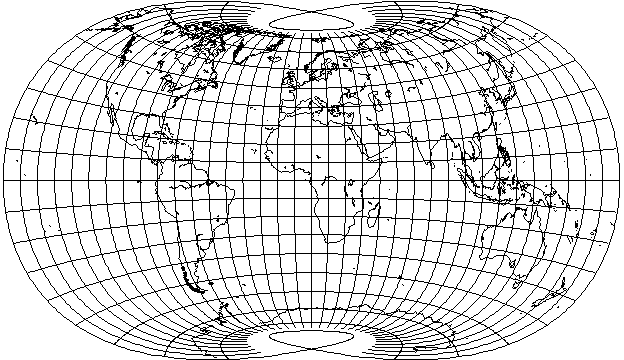
If we try basing the radii on 1/6th of the latitude, and the longitude scale on 5/6ths of the latitude, we obtain:
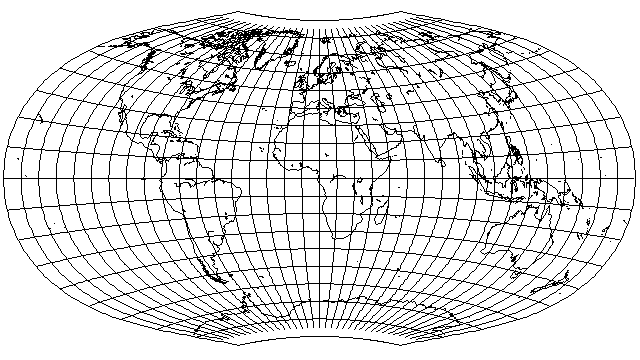
To remove the traces of Bonne's projection-style puckering near the pole line, we can return to basing the longitude scale on 3/4ths of the latitude, but continue to curve the parallels more strongly by basing the radii on 1/6th of the latitude, to obtain:
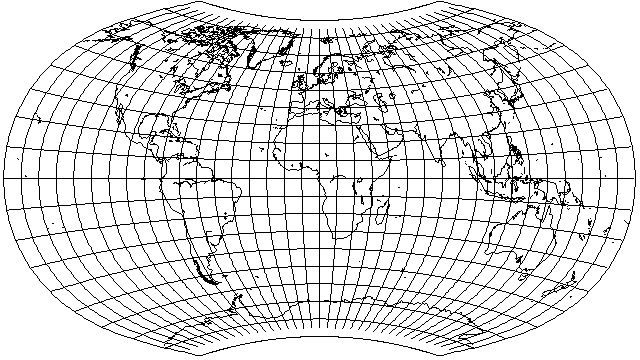
This looks like an attractive projection with no need of vertical stretching. However, if it is desired to make the vertical versus horizontal proportions accurate for, say, 45 degrees of latitude, the required amount of stretching is easy to calculate from the fact that the longitude scale is based on 3/4 of the latitude: simply take cos(33.75°)/cos(45°) as the factor, or 1.1758756... .
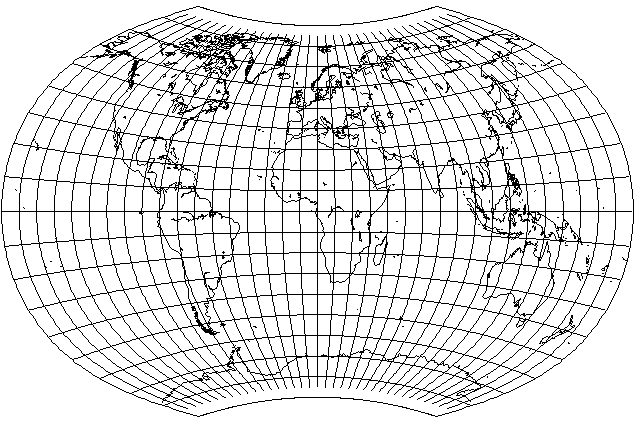
This turns out to be a significant amount of stretching; making the standard parallel 50° instead would have required even more.
To reduce stretching, but still to favor the economically developed areas somewhat, yet with a nod to balance, I thought that perhaps a standard parallel of 35° might be worth a try. Here, the factor of vertical stretch is only 1.09487945... .

This does seem to me to strike a very nice balance.
Another attractive combination of parameters is the one which yields the following:
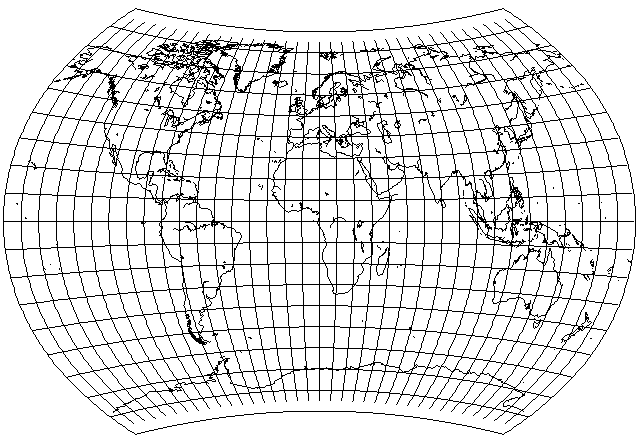
Here, the radii of the parallels are based on 1/12 of the latitude, and the longitude scale is based on 3/5 of the latitude, and there is a final vertical stretch of 1.2. This resembles, but does not quite match, the Polish Army Topographical Service Projection which appeared in the Pergamon World Atlas.
I could not find the original paper by Wiktor Grygorenko describing the projection, but a paper about the atlas in which it was used reproduced one illustration from that paper, giving clues which I used to attempt to approximate the way in which the projection was rounded. I had some difficulty in doing so, but I ended up with this attempt at an imitation:
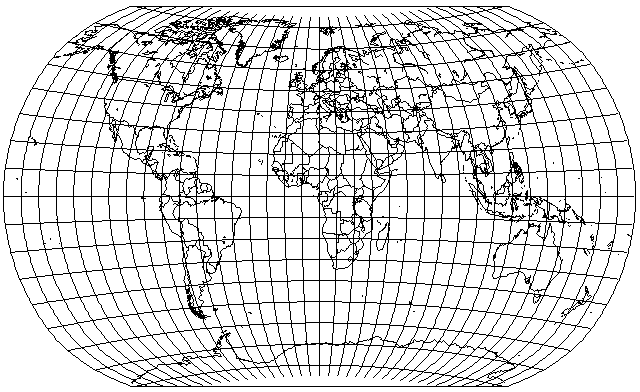
The atlas in which this projection appeared was considered to be one of the world's great atlases. But there is a sad story connected with it: for some reason, an accusation was made by individuals within Poland's ruling Communist regime against those working on the atlas that they were plotting to show Jerusalem, rather than Tel Aviv, as the capital of Israel, leading to the team that worked on it being dispersed, and the materials used to create the atlas becoming in many cases lost, so that Poland lost the opportunity to be the host of one of the world's major publishers of atlases.