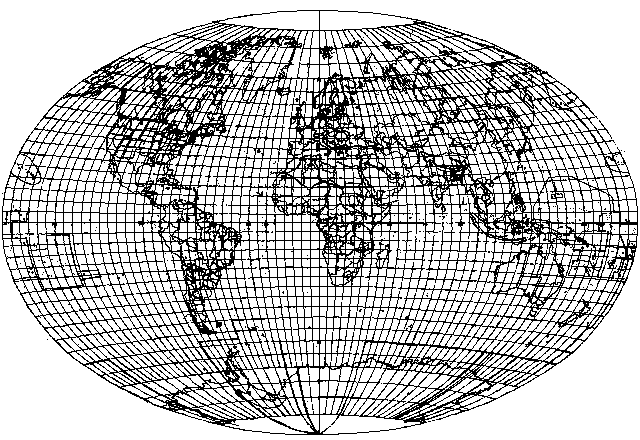
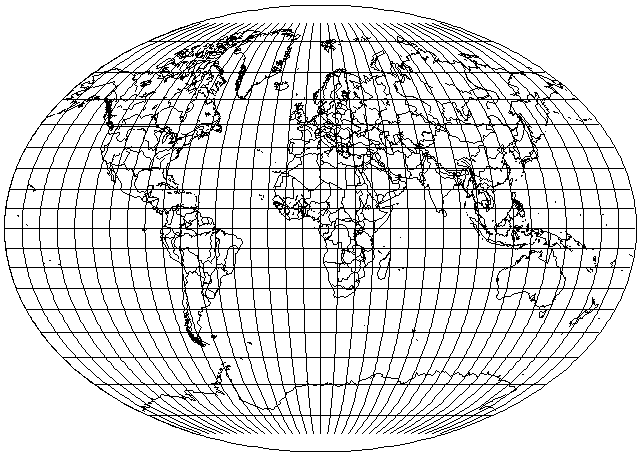
Because several equal-area projections, such as the Hammer-Aitoff projection, project the world into an ellipse twice as wide as high, and the Van der Grinten projection, which closely resembles the conformal Mercator, projects the world into a circle, I was inspired to construct a projection of the world in an ellipse one and one-half times as wide as it is high for a better compromise between those two goals.
However, I am hardly the first person to have that idea; several of Kavraisky's projections use the ellipse of that aspect ratio as well. Also, I have since learned of the Fahey projection; although that projection is a pseudocylindrical, it is somewhat similar in its general compromise between conformality and equal-area to this one.

This map projection is conventional, and it is neither conformal nor equal-area. It is a compromise projection, providing an attractive presentation of the whole world on an ellipse 3 units wide by 2 units high.
The horizontal scale on the equator is constant.
The vertical scale on the central meridian is a cubic polynomial, chosen so that where the central meridian crosses the equator, the vertical and horizontal scales are equal, but the scale expands so that the poles are at the top and bottom of the ellipse.
If the formula for longitude on the equator is:
x = longitude
then the formula for latitude on the central meridian is:
y = latitude + (30 degrees) * ((latitude/90 degrees)^3)
On the bounding ellipse, a constant vertical scale is used for latitude which is 4/3 as large as that used for longitude on the equator.
The parallels of latitude, other than the equator, are then constructed by joining the two points on the bounding ellipse and the point on the central meridian for the given latitude by a circular arc.
Points on that arc are then assigned longitudes by using a constant horizontal scale, dividing the whole arc from its two ends intersecting the bounding ellipse into 360 degrees.
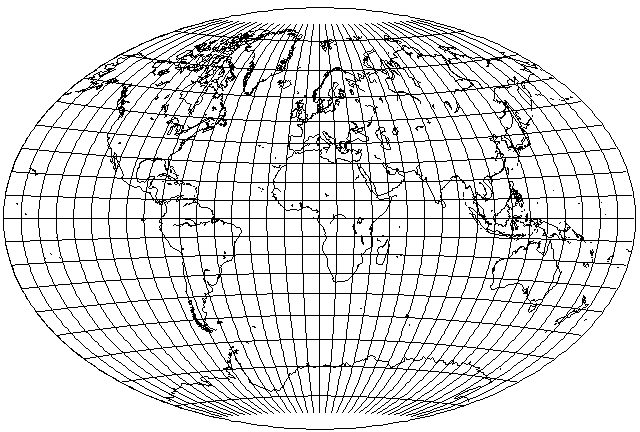
For comparison with the other projections described on these pages, instead of the hand-drawn image above, here is this projection as drawn using the same program as used for the other images:
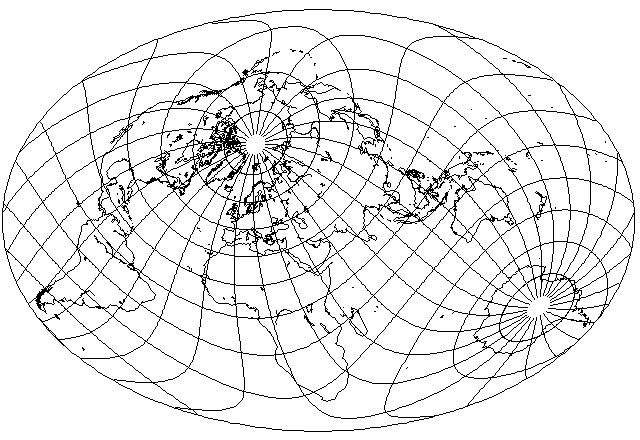
Of course, this projection can also be drawn on a computer as well, and it can appear in its oblique aspect:
Inspired by such projections as Craster's Minimum-Error Polyconic, and the Aitoff-Wagner projection, as well as by the Van der Grinten IV projection on the other hand, I tried to develop a conventional projection with a pole line.
The result is the following:
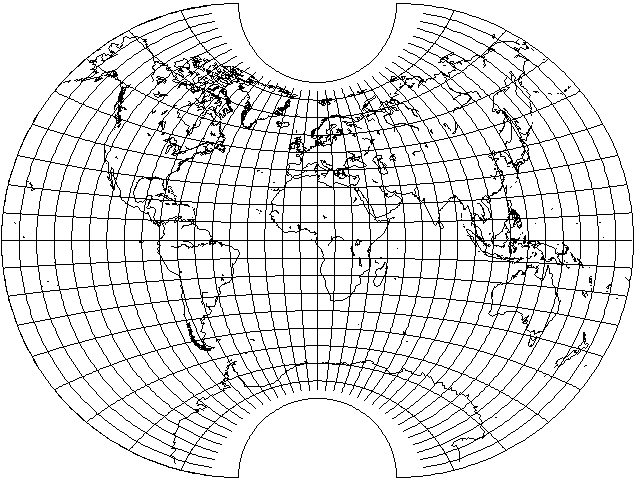
after playing with the parameters.
The equator is divided equally by longitude, and the central meridian is divided equally by latitude.
The pole lines are divided equally by longitude. However, it seemed like I could at least remove horizontal stretching around the central meridian by adopting a different strategy, making the circles for the meridians intersect the central meridian at a point above the pole, but this made the behavior of the projection in polar areas too irregular.
The place where the parallels intersect the outer meridians is specified in terms of an angle on those semicircular arcs. First, the sine of the latitude is taken as y. The angle on the outer meridians is taken to be the arcsine of 2/3 y plus 1/6 y cubed plus 1/6 y to the fifth power. At first, 1/3 y cubed was used, and then 1/3 y to the fifth and 1/4.5 y cubed plus 1/9 y to the fifth were compared.
Here is an oblique version of the projection, which allows its distortions to be more readily seen:
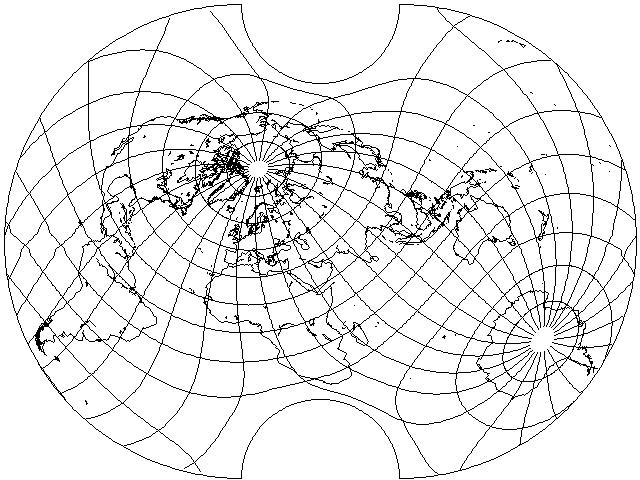
For another example of a projection in the same general area, this is the arithmetic mean of Aitoff's projection with the van der Grinten projection:
The boundary is not an ellipse because corresponding points on the boundary of either one of the two projections being averaged for the same latitude aren't at the equivalent position on the boundary of the other projection involved.
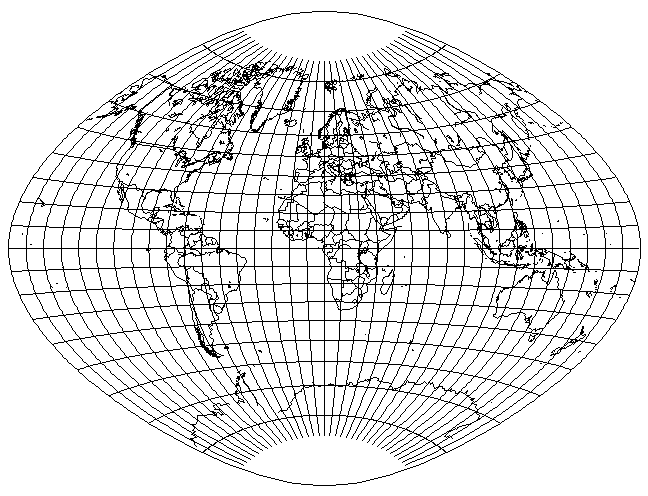
A projection that does put the world in an ellipse, but one with a slightly less elongated aspect ratio, of 1.414638:1 instead of 1.5:1, is the Fahey projection:
This is a pseudocylindrical projection.