At the time when the best known of the Van der Grinten projections, actually the Van der Grinten I projection, but usually just known as the Van der Grinten projection, was announced, three other projections were also described. While two of them seemed to me to be not of much interest (in fact, although the graticule of the whole projection looks odd, the Van der Grinten III has also been used in a number of places with a fair degree of success, and it can be claimed to have better properties than the original Van der Grinten), the Van der Grinten IV projection is an interesting conventional projection which does not share the strong bias towards shape and against area of its more famous companion.

The construction of this projection is illustrated in the diagram below: note that the arcs are drawn through a point on the central meridian (which is divided equally) and a circle, not the boundary of the map.
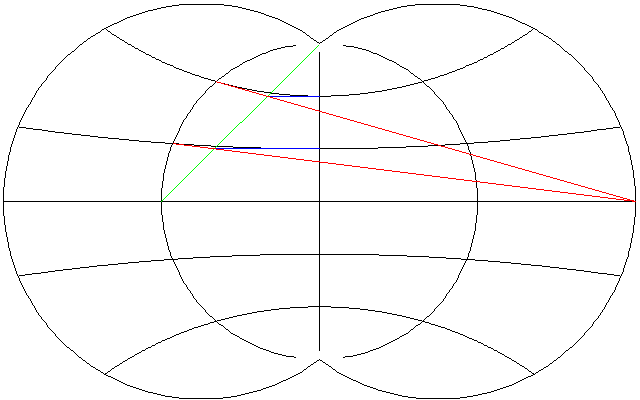
The red lines satisfy the equation
y lat
--------- = -----------
x + 180 270 - lat
and the circle they intersect satisfies the equation
2 2 2 x + y = 90
so the location of the points on the circle that determine the arcs of the parallel is found by means of a quadratic equation, derived by substituting for y:
Denoting the ratio above by q, as follows:
lat
q = -----------
270 - lat
we substitute as follows:
2 2 2 2 x + q (x + 180) = 90
obtaining the quadratic equation:
2 2 2 2 (q + 1) x + 360 q x + (32400 q - 8100) = 0
which can then be solved by the usual methods.
Note that the parallels near the equator have a very large radius. Thus, the vertical scale on the equator remains uniform, rather than being allowed to increase near the edges of the projection; this is part of the design of this projection in order to preserve shapes.
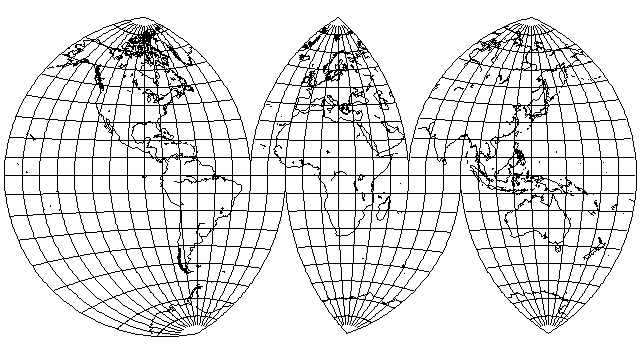
Even though this projection is not pseudocylindrical, therefore, it should be possible to interrupt the Van der Grinten IV projection, or, in fact, the original Van der Grinten projection, which also has this characteristic. The result of doing so would be as shown in the diagram below:
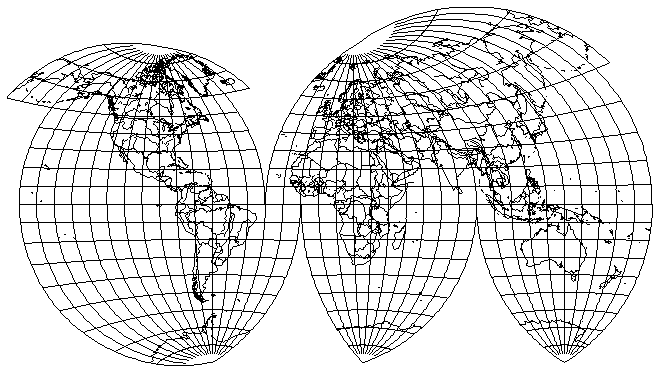
It is clear that there is no sudden jump in scale anywhere at the Equator. But because the choice of standard meridian for each of the areas interrupted allows freedom in exaggerating scale, as illustrated above where no interruption is allowed to divide Eurasia, while the standard meridian is kept in Europe, considered as important, so that only one area of the whole map is exaggerated greatly in scale, Siberia, and even China to the south of it is enlarged to a far greater degree than anywhere in Australia, Africa, or the Americas. Thus, this could be considered by some as a particularly deceptive map projection.
With a little effort, though, this trait can be moderated somewhat:
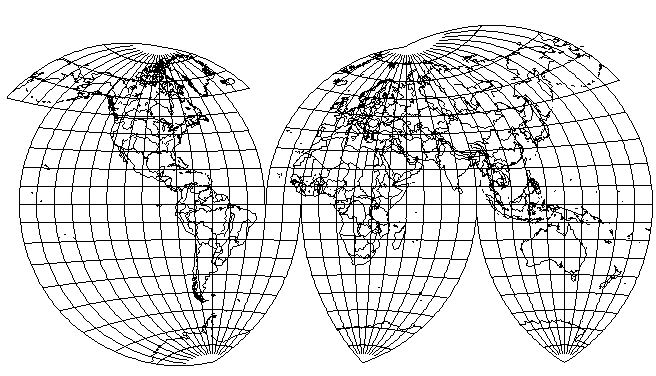
A more genuine determination to be fair and balanced would produce a map like this, with the drawback that Europe experiences considerable shear:
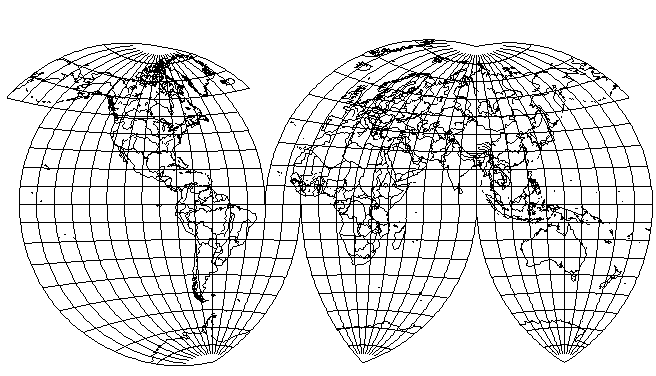
Of course, if one throws both caution and shame to the winds, one can reduce the degree of interruption to keep the North Atlantic together, and have less shape distortion, by using an uninterrupted modified Van der Grinten in the Northern hemisphere, interrupting only the Southern hemisphere:
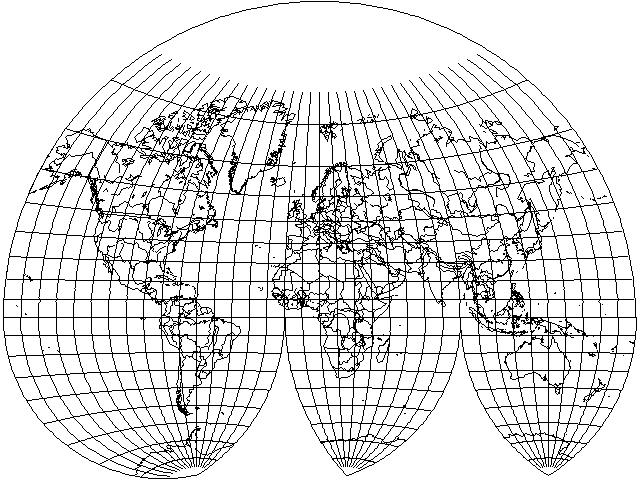
Note also that the globular projection, mentioned below, could not be interrupted in this way without discontinuities of scale at the Equator.
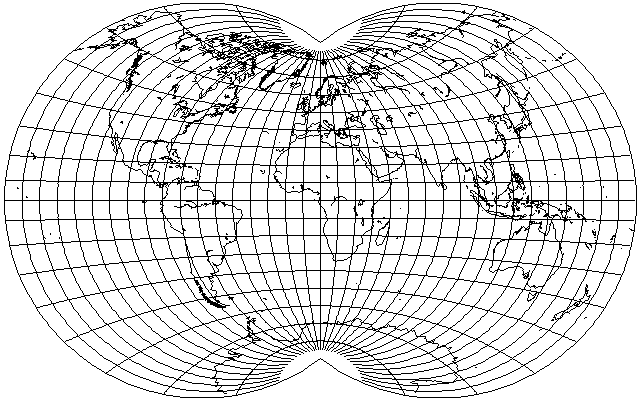
The globular projection, if extended to cover the whole world, instead of being used in its usual format to cover only a hemisphere,
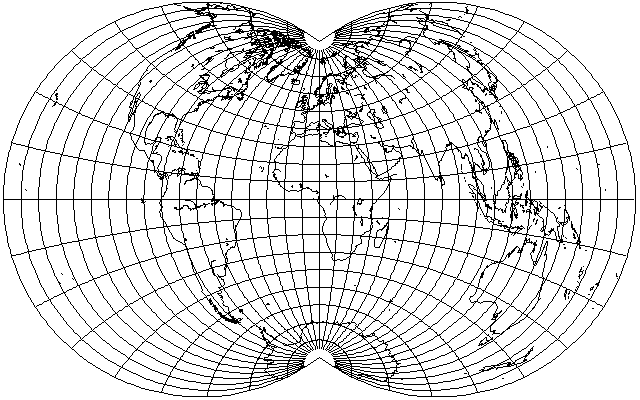
has the same outline as the Van der Grinten IV projection, but the less rapid expansion of the parallels in the Van der Grinten IV clearly makes it a more attractive projection.
The Van der Grinten IV projection is relatively obscure, but a subroutine for drawing it is included in the program GRASS, and I thought I had seen some climate maps drawn with this projection in one German-language atlas.
I have since learned, though, that my memory may have been playing tricks on me, and the book I saw may have been the unique and unusual book Grundzüge der allgemeinen Wirtschaftsgeographie by Bruno Dietrich from 1927. However, that book is described as being "illustrated with many full-page thematic maps", and I do quite distinctly remember seeing the maps in whatever book I saw being generally two to the page when in this projection.
In any case, the projection used in that book differed from the Van der Grinten IV by apparently being equal-area; while the method of projection was not described, the mathematical cartographer Kozo Kitada worked out the method for drawing an equal-area projection having the same general characteristics as the one used in this book.
The search result from which I learned this was a post in the Mapthematics forums by the "celebrity cartographer" Daniel Strebe, and he referred to the projection as the Dietrich-Kitada projection, the name by which it is now known.
Although an attractive projection, still there is quite a bit of shear and thus it is likely that Winkel's Tripel, for example, would normally be preferred to this projection. However, it occurred to me that if I allowed a degree of tilt towards the conformal, but not as much as in the Van der Grinten I, quite an attractive projection could be obtained.
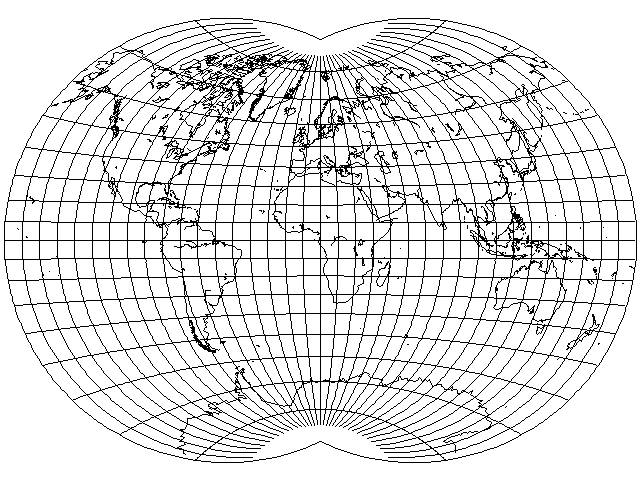
Here, the central meridian is divided as in the Stereographic, with the parallels then derived from the central meridian position, and the meridian positions suitably scaled. Thus, this projection is conformal at the central meridian, and can be mated with the stereographic.
However, a less extreme modification, which preserves the uniform scale of the central meridian, is also possible. Instead of projecting the lines from the point on the edge of the map 180 degrees away from the central meridian, increasing that distance to 360 degrees produces a generally more pleasing projection, although with more shear in some places:
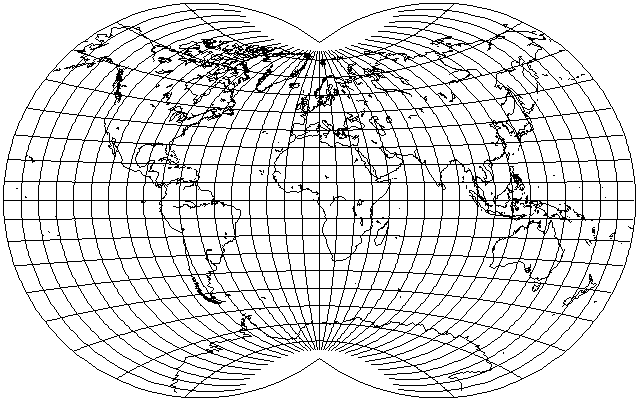
However, looking at this has led me to the conclusion that a better projection would be found somewhere in between that and the original Van der Grinten IV projection, so I tried again with a distance of 270 degrees, and obtained the following:
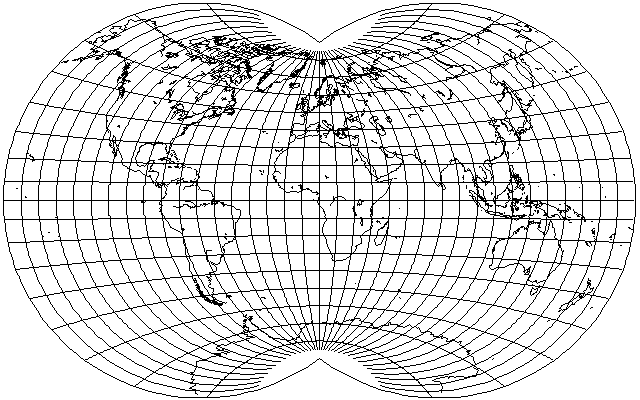
which I find to be quite reasonable.
Since this projection seems to do quite well, here is my standard oblique case (which places southern Africa near the South Pole in order to avoid interrupting Antarctica, which is why you likely haven't seen this kind of oblique projection before) for comparison and for a new view of its distortions, even though conventional projections aren't usually used in oblique or transverse cases, since that defeats the primary purpose of their design, making them easy to draw:
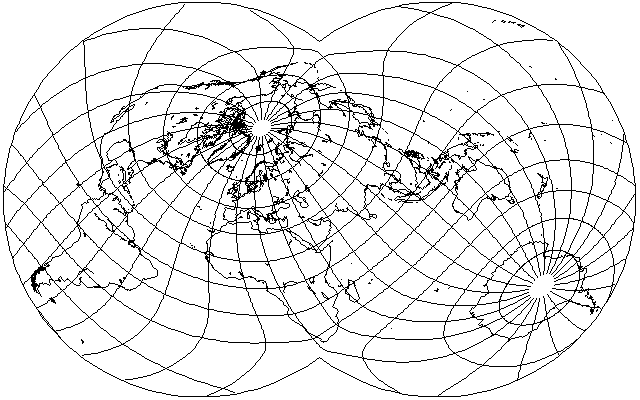
However, the experience above with the interrupted Van der Grinten suggests that although at the extreme ends of the projection, there is vertical stretching that a longer projection distance will reduce, in the middle part, there is a more objectionable vertical squashing. Thus, a shorter projection distance might be tried; perhaps 90 degrees:
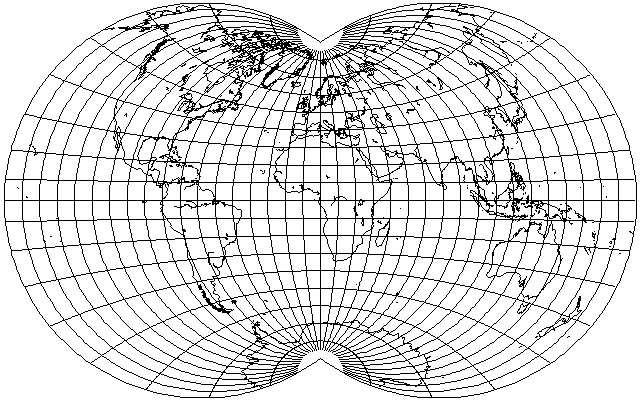
or with a more moderate change to 120 degrees:
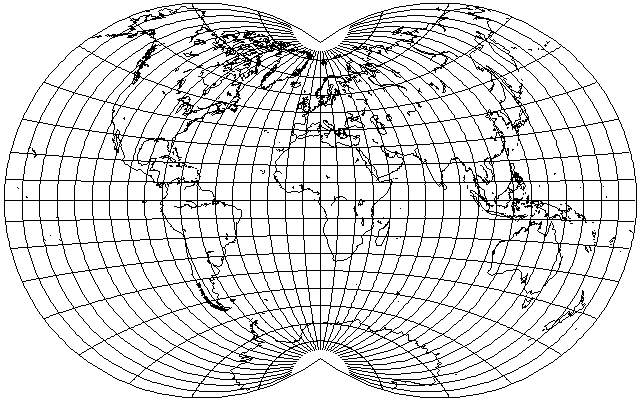
Using the latter change, and only replacing the wider areas between interruptions of the Northern hemisphere, the interrupted Van der Grinten above becomes:
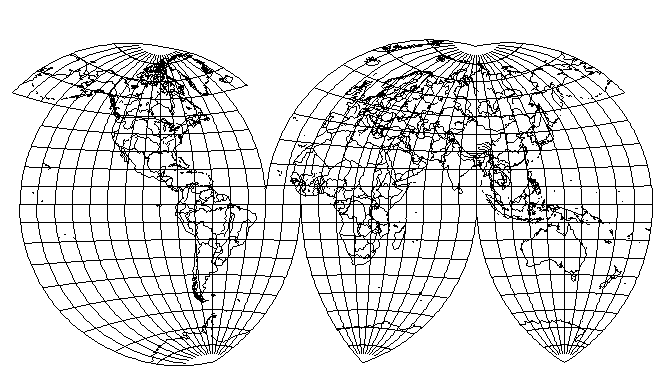
The improvement in North America is quite clear, but although there is a slight improvement in Europe, the benefits are limited.
Here, though, it is apparent that the standard meridian was moved a bit too far to the East in the name of even-handedness, and an improvement can be obtained without leading to a projection as unbalanced as those shown above as follows:
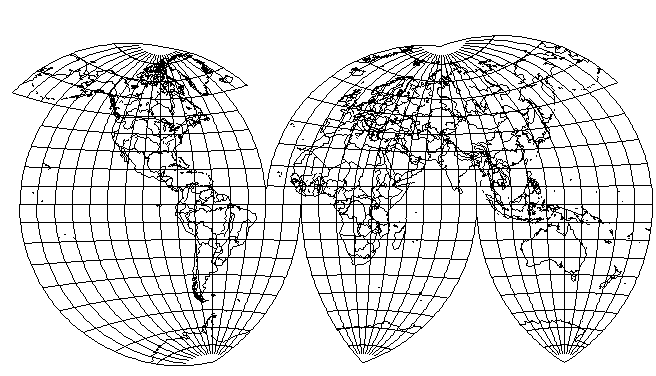
Alternatively, if one uses more frequent interruptions, at least in the case of the Northern half of the Eastern hemisphere, the projection distance of 90 degrees does work out well: