Since the Mercator projection causes considerable distortion of size at latitudes approaching the poles, many attempts have been made to create map projections which, although similar to it, improve upon it in this respect.
One such projection, which has appeared in a number of British atlases, is Gall's projection. This projection uses the stereographic projection, which we will encounter later:

and which is the conformal azimuthal projection, as the guide for how rapidly the parallels should spread apart in it. Since it is cylindrical, and not azimuthal, of course, this does not yield a conformal projection.
Gall's projection looks like this:
Note that because the northern and southern parts of the map are stretched horizontally, the map as a whole was stretched vertically; in this way, while tropical countries are stretched vertically, the map's standard parallels, where the stretching is balanced, are at 45 degrees north and south, allowing the temperate countries to be shown well.
Here is an example of Gall's Stereographic Projection in use,
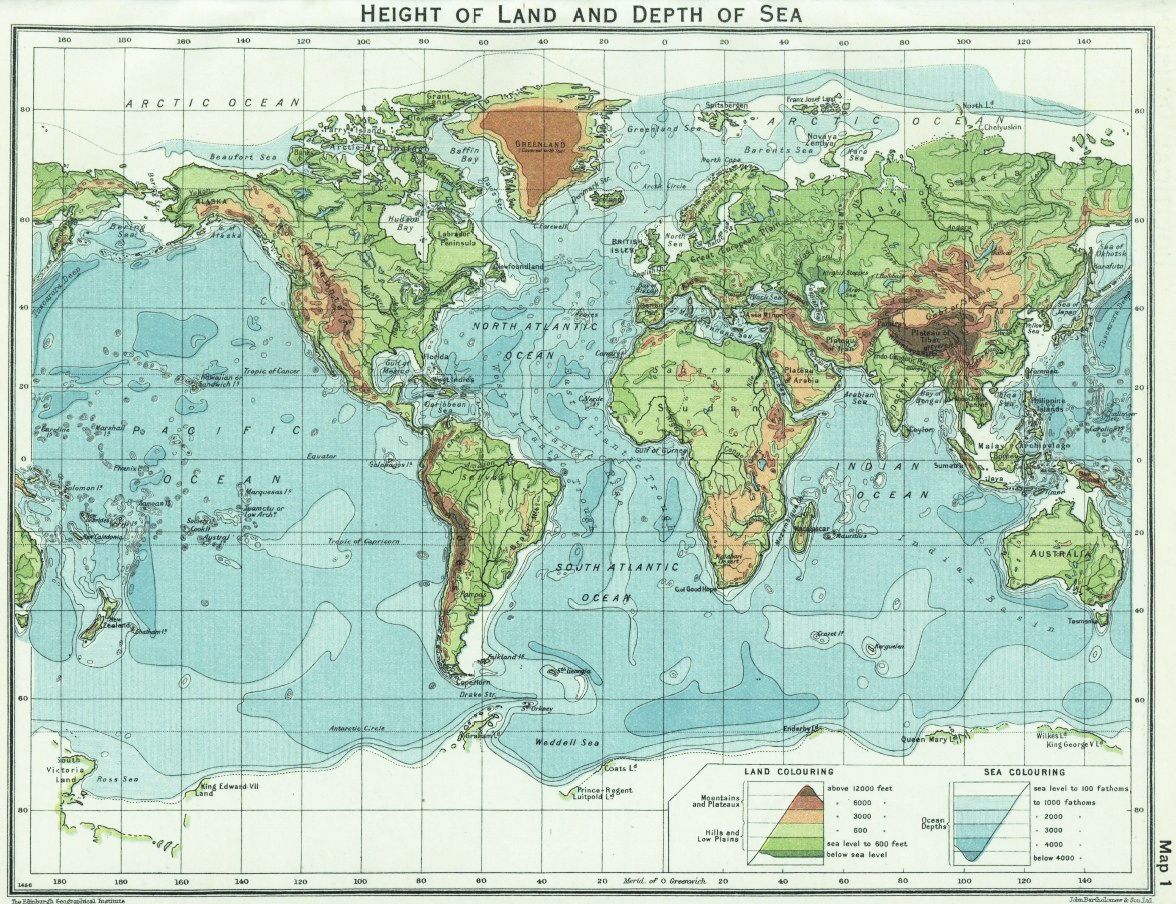
for a physical map of the world in a school atlas from 1929.
If we don't stretch the map, we get Braun's projection:
and I must admit I generally prefer projections not to be stretched overall in the fashion of Gall's projection. Thus, I will be showing the Plate Carré and Cylindrical Equal-Area projections with the Equator as their standard parallel in forthcoming pages. Some projections with such an overall stretch, though, were too notable to exclude, and do not have an alternate form without it, specifically the Mollweide projection and the Eckert IV projection.
Actually, I've since learned that modifying the Mollweide projection so as not to have a vertical stretch at the Equator has been done, the result being known as the Bromley-Mollweide projection.
Since the Gall Stereographic projection does not have the precise properties of the Mercator projection, namely conformality and true loxodromes, cartographers have felt free to take some liberties with it to produce a more attractive projection.
Thus, the noted geodesist Guy Bomford devised a pseudocylindrical projection which modified the Gall Stereographic projection by curving the parallels so as to produce a small narrowing of the projection near the poles:
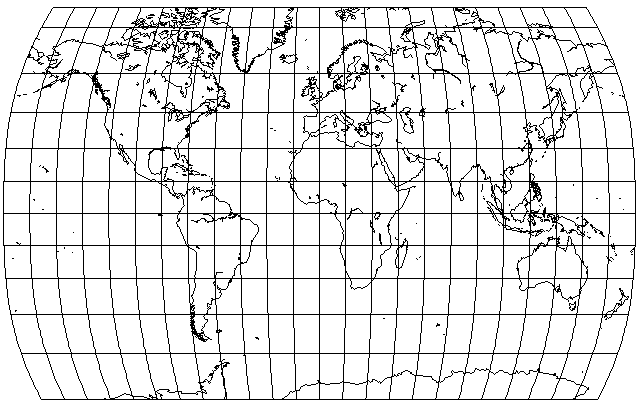
A map on this projection was used for the map illustrating world time zones in the Oxford School Atlas for many years.
Earlier than that, during the 1930s, in Canada a wall map, 26 1/2 inches high and 36 inches wide, based on the Gall Stereographic projection, but with the North polar regions modified so as to render them narrower was drawn by the Hydrographic Service, first for the Department of Mines and Resources, and then for the Department of Trade and Commerce.
That map looked something like this:
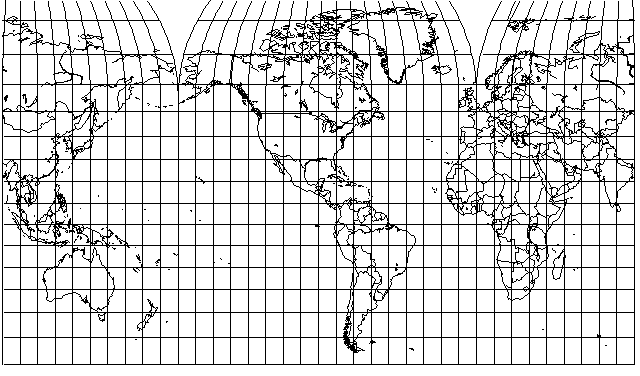
It was used as the basis for the world map in a curious atlas offered as a premium by Monarch Flour. Except for the map of Canada, on a conic projection, and an oblique azimuthal equidistant centered on London, England of air routes on the back cover, all the maps in that atlas were on the Mercator projection.
But the world map, instead, was on a slightly modified version of the Gall Stereographic.
We've looked at the Braun projection, where the vertical stretch applied to the map is omitted. Instead of modifying the Gall Stereographic to that extent, a Soviet atlas from 1937 used a version where the standard parallels were at 30 degrees North and South latitude. This reduced the amount of stretching in the tropical regions enough so that it was no longer visually objectionable, at least in my opinion.
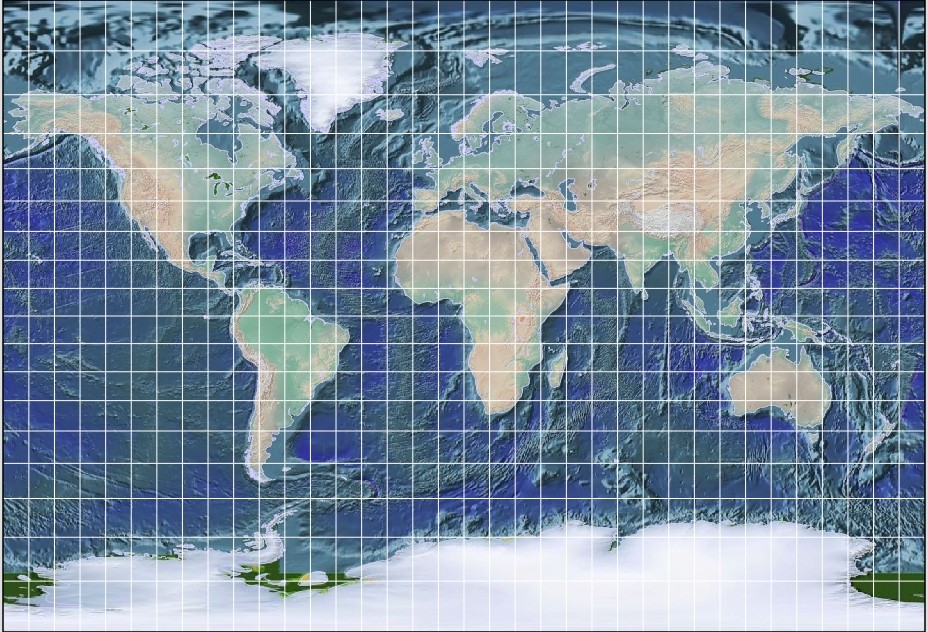
This projection is known as the BSAM projection, from the Russian name of the atlas, the Great Soviet World Atlas (Bolshoi Sovyetskii Atlas Mira), in which it appeared.
And here is an actual example of that projection in use within that atlas.
The perspective point for the Gall Stereographic is behind the tangent point by the full diameter of the globe; a good approximation to the Mercator projection involves a perspective point that is behind the tangent point by 3/4 of the diameter of the globe.
Since making the standard parallel 40 degrees north and south causes too much stretching in the equatorial regions, what if a projection were used that was intermediate between the Mercator and the Braun projection or the Stereographic Cylindrical?
Here is what a perspective cylindrical looks like (without stretching) for a perspective point that is 7/8 of the diameter of the globe behind the tangent point:
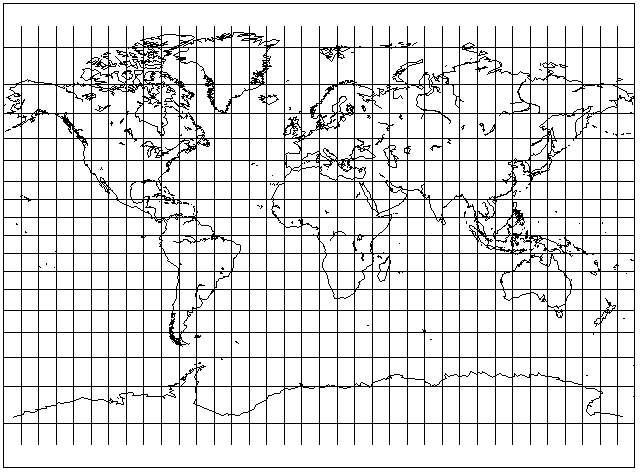
That is, it's without vertical stretching, so the Equator is the standard parallel. It resembles the Miller Cylindrical Projection, which we will see on the next page.
However, improving on the Mercator this modestly is sufficiently out of fashion, I had not felt it worthwhile to work out the degree of vertical stretching required for a 40° standard parallel, in order to offer an improvement on the Gall Stereographic Projection.