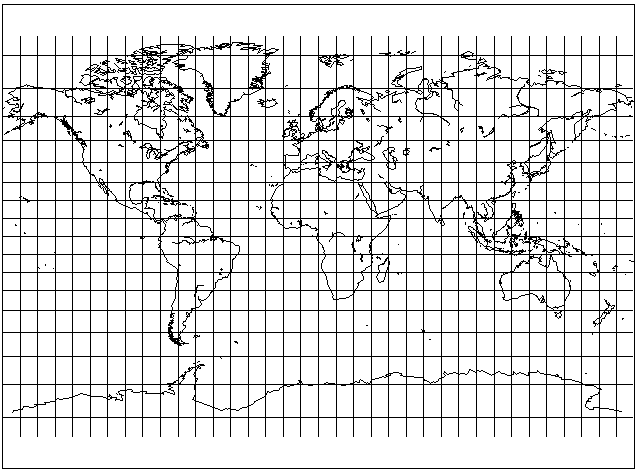
This is another projection that attempts to be a somewhat more moderate replacement for the Mercator projection. It allows a somewhat more rapid increase in scale than the Gall projection, however, so that there is no need to stretch the projection as a whole to improve the appearance of the temperate regions. It has the following appearance:
This projection works by using the formula for the Mercator projection, and modifying it. Each latitude is treated as if it is the latitude that is only 80% as large as itself. Then the projection is stretched vertically, but only by 25%, to compensate for the factor of 80%.
The Miller Cylindrical projection was devised by noted cartographer Osborn Maitland Miller in 1942. A book about cartography noted that one significant use of that projection was in the Esso War Map; I have found that this map may be viewed online on this page.
As noted on that map, it was also the first public use of that map projection.
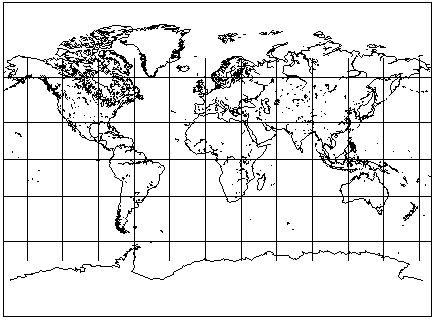
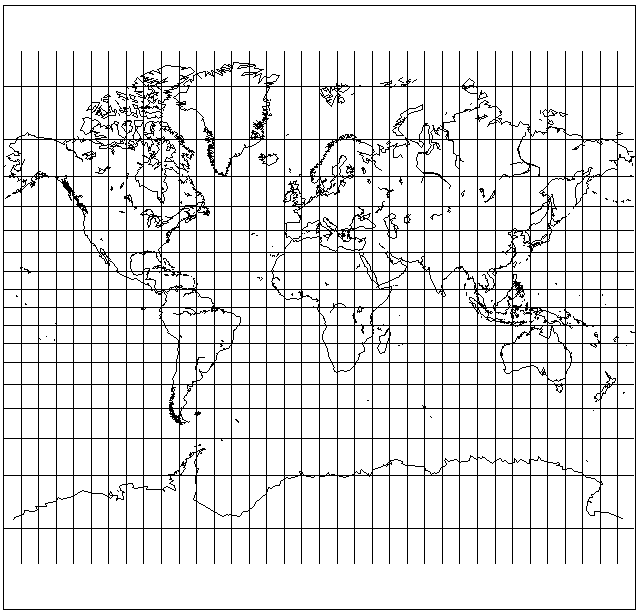
Here is an example of a map using the Miller Cylindrical Projection:
This map shows that the projection is very handy, at least, for diagrammatic maps which have as their purpose showing where things are on the Earth, where distortion is not a primary consideration.
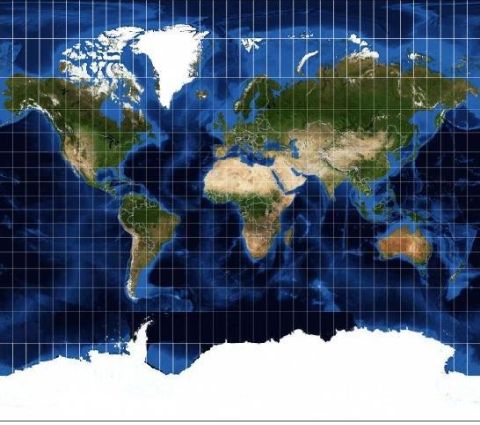
The Miller Cylindrical Projection was used as the basis for the Patterson projection, shown below as drawn by G.Projector:
developed by the team which also produced the Equal Earth projection.
From the Equator to 55 degrees N and S, it follows the Miller projection, and then the expansion of the vertical scale ceases as one goes further towards the poles, and then the vertical scale starts to shrink at a point even further north and south.
In the paper describing the precursor to that projection, the Compact Miller projection, which doesn't include the additional compression of vertical scale closer to the poles, they note the same principle was used in the Kavraiskiy I projection, which followed the Mercator betweem 70 degrees North and 70 degrees South, and then became a matching equirectangular (or Plate Carée) projection beyond that.
That projection would look something like this:
and the program G.Projector should not be blamed for my clumsy job in stitching together its output.
These projections inspire me to suggest a similar projection that would seek to keep its stretching unnoticeable without going quite as far as the Kavraisky I:
Follow the Mercator up to 50 degrees of latitude; between 50 degrees and 65 degrees, use the Miller Cylindrical projection, stretched slightly so that 50 degrees would be its standard parallel, and then from 65 degrees to the poles, use a matching equirectangular projection.
However, I have also been inspired to suggest another modification to the Miller Cylindrical Projection, one that will not change its appearance as much.
The perspective cylindrical projection, with a projection point located at 3/4 of the diameter of the Earth below the ground,
is known to be quite a good approximation to the Mercator projection.
Since the Miller Cylindrical Projection, unlike the Mercator projection, does not have any specific properties such as conformality, then, if the 3/4 perspective cylindrical projection is easier to calculate than the Mercator (this is not necessarily true, but it can be constructed by geometrical means, and thus it may be simpler if you're not using a computer), why not use the 3/4 perspective cylindrical projection instead of the Mercator as the basis for the Miller Cylindrical? The result will be only very slightly more compressed towards the poles, and, thus, will look just as good:
