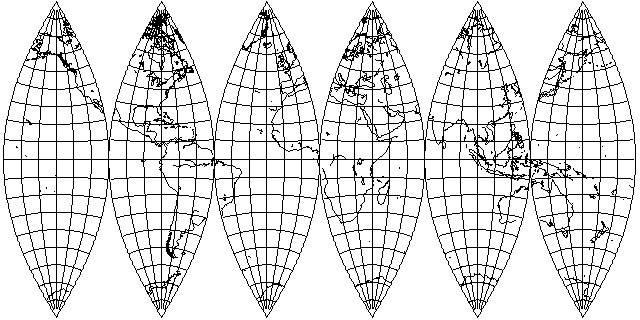
As noted in the first page of this chapter, I feel that this projection, and the closely-related modified versions of it, belong to a class of projections as fundamental as the cylindrical, the conic, the azimuthal, and the pseudocylindrical and the pseudoconic.

It was described by its inventor, Ferdinand Rudolph Hassler, in an 1825 paper. Hired by the United States Government in 1807 to carry out a survey of the coast of the United States, and later dismissed from it for several years, and then called upon to return to that survey, he organized what later became the United States Coast and Geodetic Survey, and in the interim he made crucial contributions to the standardization of weights and measures in the United States.
It can be, easily enough, dismissed as merely a conventional projection which serves as an easy-to-construct substitute for the transverse case of the Plate Carrée (Cassini's Projection). And indeed, that basically is its main usefulness.
However, the fact that it preserves the correct curvature for the representation of each parallel seems to me as worthy of a specific classification as the characteristics which identify azimuthal, cylindrical, and pseudocylindrical projections.
In a way, if the Sinusoidal projection and Bonne's projection can be thought of as a cylindrical or conic projection trying to be an azimuthal projection, the Polyconic can be thought of as a cylindrical projection trying to be a transverse cylindrical projection.
Also, the Polyconic seems to have a particular appeal to the eye, perhaps deriving from the true curvature of each parallel. Thus, star maps have been constructed with a similar layout to that of the world map above. Also, it is often used for making the gores from which globes are constructed. (The illustration here uses gores too wide for constructing a proper globe; gores of half this width are in common use for that purpose.)
The Polyconic projection, as noted above, has its lowest distortion along its central meridian. So it's an ideal projection for a map of Chile or Argentina. And sometimes it seems that some people think that this is all that it is good for. But if it is a substitute for a cylindrical projection, it should not be forgotten that although cylindrical projections are at their best along the Equator, they are often used for maps of the whole world.
For historical reasons, basically due to tables of coordinates for the projection published by the U.S. government, a number of atlases have included maps of the United States of America drawn on the conventional Polyconic projection, looking like this:
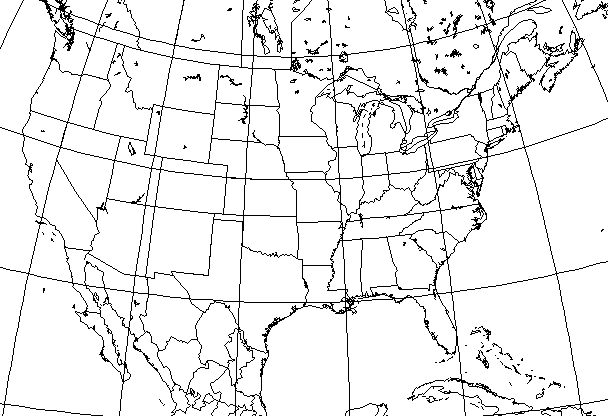
It is not incorrect to say that this is a misuse of the Polyconic projection. The 48 contiguous states are wider than they are long, so they would be better served by, say, a Simple Conic projection than by a Polyconic. However, the United States are small enough so that the result is not too terrible in appearance despite the mistake.
This map
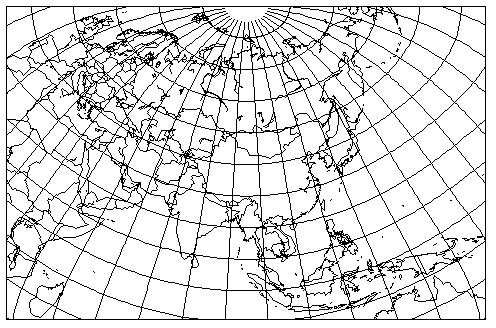
resembles a map of Asia published in 1942 by the National Geographic Society.
This map is obviously not drawn on a Polyconic projection in the conventional aspect. Instead, it is a Transverse Polyconic; the Equator of the projection is the meridian of 95 degrees East longitude, and the central meridian of the projection is a horizontal line centered at 95 degrees East longitude and 40 degrees North latitude on the map.
This is not, technically, a misuse of the Polyconic projection in the way that the map of the United States was. The area is wider than it is high, so it is longer in the direction of the central meridian of the projection, because that has been rotated - to keep North at the top in this transverse aspect - to be horizontal.
But it certainly is covering a much larger portion of the world than it is usually thought that the Polyconic projection is suitable for.
Partly, this is because of a habit of thought; one of the chief uses of the Polyconic projection was for very large-scale maps before it became practical to use the Transverse Mercator for that purpose instead.
Obviously, even if one disapproves of using the Polyconic in this way, this is clearly a much better map than would have resulted from using Bonne's projection in its conventional orientation for a map of this same region, which is what likely would have been done in older atlases - with the Stereographic projection, relatively easy to draw in an oblique case, being the other possible alternative.
On the previous page about the Mercator projection, we saw how an Oblique Mercator was able to produce a very attractive map of the Americas. If the Polyconic can be used to produce a map of Eurasia, and it has behavior similar to that of a cylindrical projection, the question naturally arises as to whether it could also produce a good map of the Americas.
The attempt does bump up against the fundamental limitation of the Polyconic compared to a cylindrical projection: the Polyconic, in its conventional aspect, can cover 180 degrees, from the North Pole to the South Pole, while a cylindrical projection can girdle the entire globe. But while the vertical extent of the Americas is long, it does just barely fit, and so it was possible to produce this map:
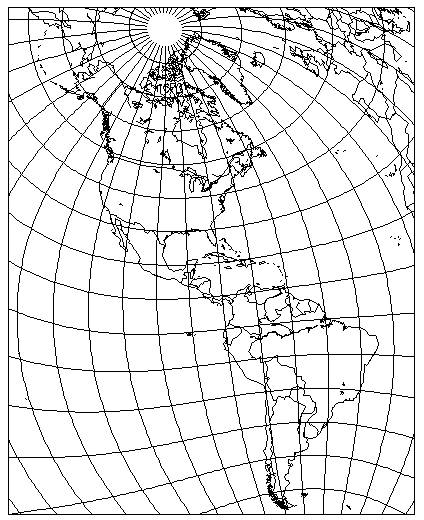
The globe is tilted along the meridian of 30 degrees West longitude by 32 degrees, and then that meridian is assigned to 49 degrees East longitude in map coordinates. The resulting map is tilted 30 degrees counter-clockwise.
To show what is going on behind the scenes,
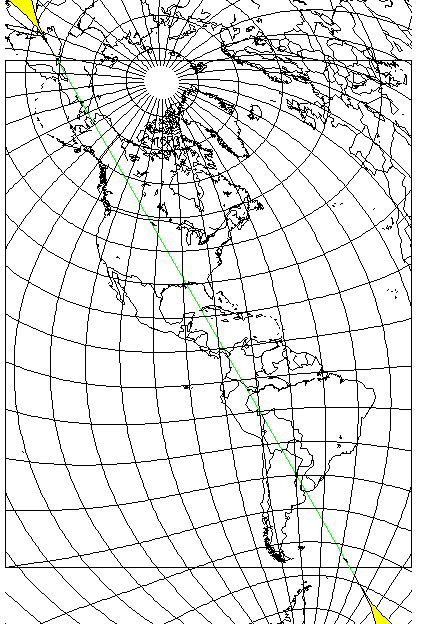
this map shows where the projection is interrupted beyond its poles, and its central meridian is shown as a green line.