Unlike the normal case of the simple conic, the polar case of the Azimuthal Equidistant, or the normal case of any cylindrical projection, the meridians and parallels do not cross at right angles in the Polyconic. This was felt to be a defect, and thus, in 1853, a version in which the scale along the parallels was modified to obtain this property, known as the Rectangular Polyconic (or the War Office projection) was devised. Usually given with constant scale along the Equator, this projection could in fact have constant scale along any standard parallel.
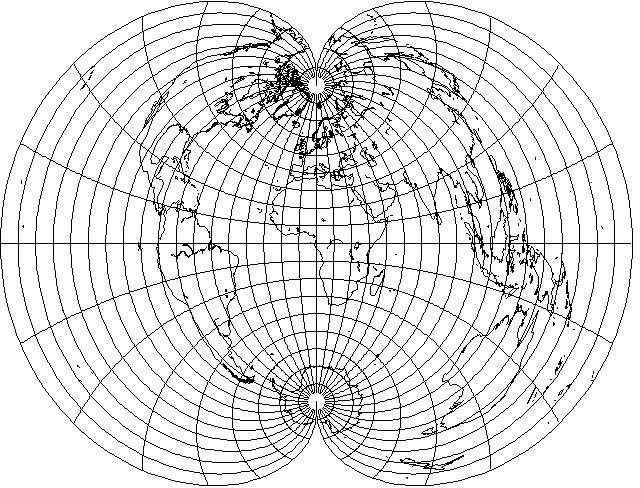
With the equator as its standard parallel, the rectangular polyconic looks like this:

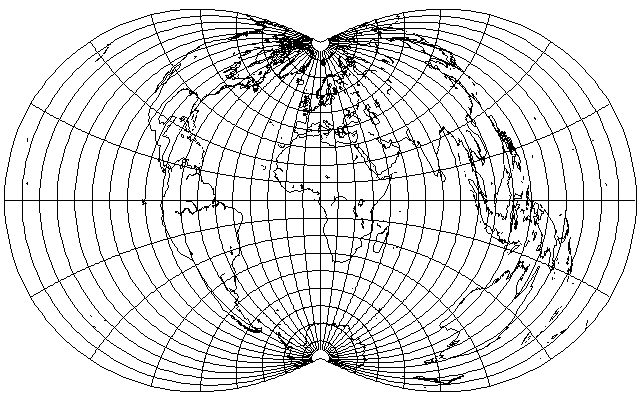
only slightly narrower at higher latitudes, and thus very hard to distinguish at sight from the simple polyconic:
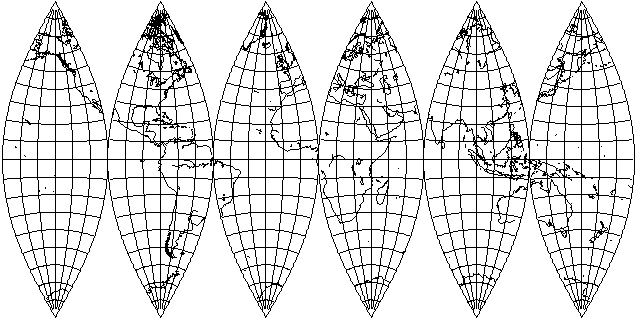
Of course, if one compares the simple polyconic for the whole world:
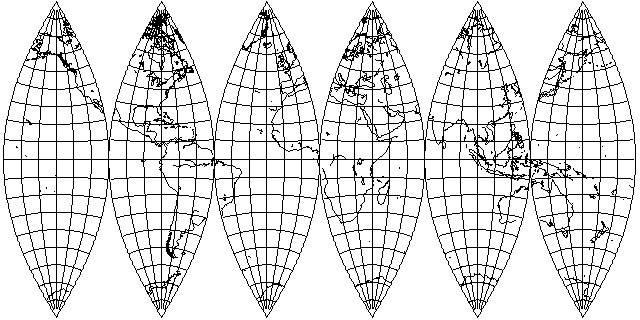
with the rectangular polyconic for the whole world,
the difference becomes more apparent.
The regular polyconic projection uses for parallels arcs whose radius is given by:
1
r = ------------
tan( lat )
and points on those arcs corresponding to different longitudes are at angles from the center from which the parallel is drawn given by:
angle = long * sin( lat )
for reasons illustrated in this diagram:
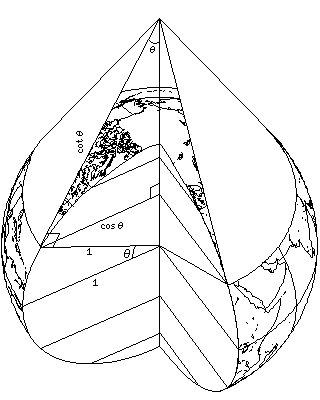
the actual radius of the parallel being cos(lat), and the radius of the arc being 1/tan(lat), or cos(lat)/sin(lat), it follows the radius of the arc is 1/sin(lat) times the radius of the parallel, so angles on the parallel have to be multiplied by sin(lat) to obtain angles on the arc.
Through somewhat complicated mathematics, for a rectangular polyconic whose standard parallel is the equator, while the arcs used for the parallels are still the same curves with the same radii, the angle along them is now given by this formula instead:
long
angle = 2 * atan( ---- * sin(lat) )
2
The chief use of the Rectangular Polyconic is in making very large scale maps; thus, it can be made with other standard parallels than the equator. For another standard parallel, the scale along the standard parallel is true, and therefore as in the simple polyconic, but the meridians are represented by the same curves as in the rectangular polyconic with the Equator as standard parallel, in order to retain the property that they cut the parallels at right angles; they merely represent different longitudes.
The simplest way to do this is to match the two projections at the standard parallel by the use of the equation:
pseudo_longitude
2 * atan( ---------------- * sin( lat_sp ) ) = long * sin( lat_sp )
2
or
long * sin( lat_sp )
2 * tan( ---------------------- )
pseudo_longitude = 2
-----------------------------------
sin( lat_sp )
and then simply use the pseudo_longitude instead of the longitude to draw the rectangular polyconic with standard parallel at the Equator to obtain the rectangular polyconic for another standard parallel.
If one makes latitude 40 (both north and south) the standard parallel, however, then,
it would be the rectangular polyconic that is the larger one if both were drawn to the same scale.
In 1921, G. T. McCaw devised a further modification of this projection; apparently, he worked out how to increase scale along the standard parallel away from the standard meridian so that the projection would be conformal along the standard parallel as well as along the standard meridian. Somewhat later, he explored the possibilities offered by the polyconic class of projections more fully.