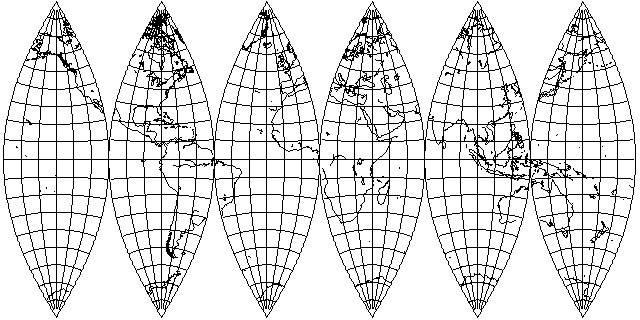
This section deals with the Polyconic projection,

and projections related to it.
Sometimes, the term "Polyconic group" has been applied to any projection which is not obviously cylindrical, conic, or azimuthal, such as the Van der Grinten or Winkel's Tripel. However, as this illustration shows:
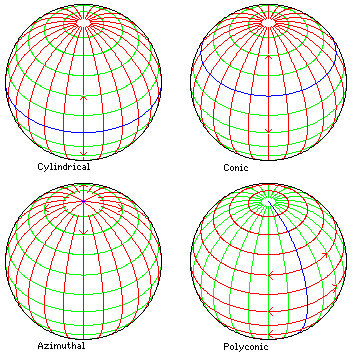
the Polyconic projection is an example of a basic scheme of projection, as fundamental as the cylindrical, conic, or azimuthal.
The blue line indicates the line (or point) of contact between the reducible surface to which the projection is made and the sphere. In the case of the Polyconic, this contact is along a great circle, so in a sense, the Polyconic can be thought of as a type of cylindrical projection.
Where it differs, however, is in the next step of the projection. A cylindrical projection next proceeds symmetrically along the meridians, as indicated by red lines, to place locations on the globe on the map. With the Polyconic, the red lines are parallels in the conventional case, so the scheme by which the globe as a whole is connected to the line of contact is different.
Note that the pseudocylindrical projections are created by starting with the blue line as a basis, using just one red line, and then changing the scale along the green lines from that red line. The same applies to the pseudoconic projections. However, Werner's projection is called pseudoconic instead of pseudoazimuthal; the term pseudoazimuthal has a completely different meaning.
One could imagine a class of pseudopolyconic projections derived from the same principle, but it would be of little use. Originally, I felt the distinguishing feature between the polyconic and pseudopolyconic should instead be whether or not the curvature of the parallels and the scale along the parallels varies in step, since this is the main property of the Polyconic.
Here is another diagram to illustrate this, this time based on the projections themselves rather than the globe:
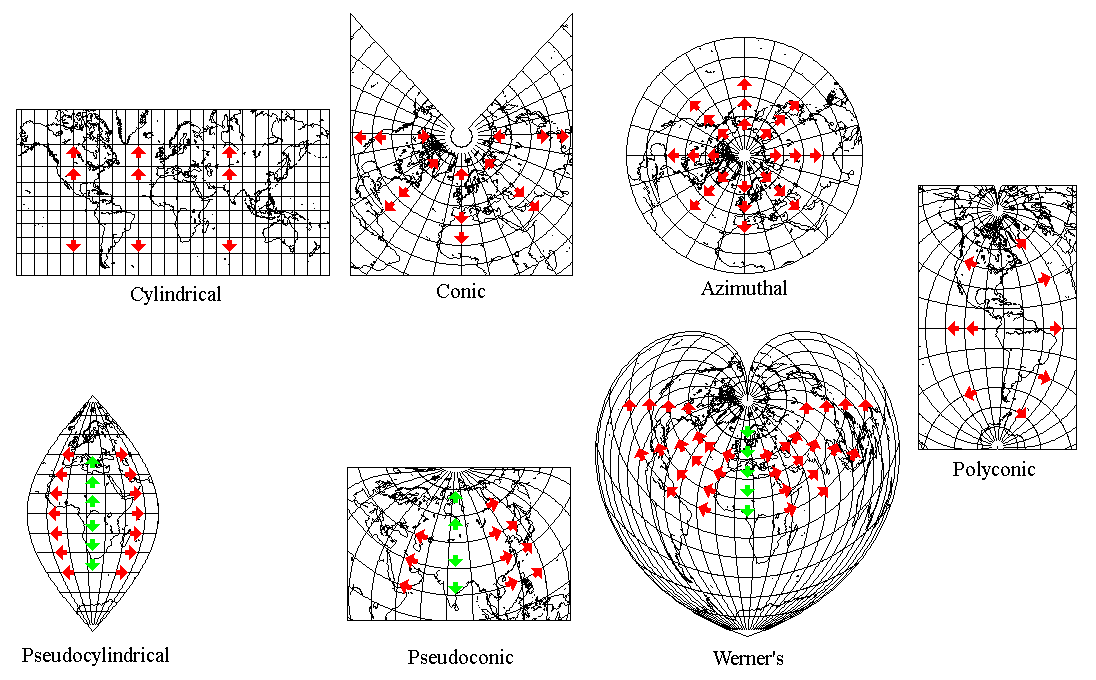
Thus:
In a cylindrical projection, everything starts from the Equator of the projection, which is of uniform scale (of course, all other parallels are of uniform scale as well). It can be of a scale smaller than true scale if two other parallels, equally above and below the Equator, are the standard parallels of the projection. Meridians are straight lines perpendicular to the Equator. Scale along the meridians is not necessarily uniform, how it varies determines which cylindrical projection one has.
In a conic projection, everything starts from the standard parallel, which is curved according to how a cone tangent at that latitude would be unwrapped. The scale along the standard parallel is uniform (again, the scale along all other parallels is also uniform), but not necessarily true; it could be smaller than true, so that scale is true on two other parallels for a projection with two standard parallels. Meridians proceed outwards from the standard parallel as straight lines perpendicular to it. Scale along the meridians is not necessarily uniform, how it varies determines which conic projection one has.
In an azimuthal projection, the starting point is the central point of tangency; meridians radiate out from it at their true angles, and the scale along them determines the type of the projection.
In a pseudocylindrical projection, first one starts from the Equator of the projection. The central meridian, only, is a straight line, and one moves along that line, in a scale that is not necessarily uniform, establishing parallels which are also straight lines like the Equator. Then one radiates out from the central meridian along the parallels; that scale is uniform, but not necessarily true, and varies with latitude.
In a pseudoconic projection, one starts from a standard parallel, moving along the standard meridian in a scale that is not necessarily uniform, establishing other meridians that are concentric with the standard meridian. Then one radiates out from the standard meridian along those parallels, in a scale that is uniform for each parallel.
In Werner's projection, one starts from a pole, moving along the standard meridian to establish other meridians with the pole as their center. Then one radiates out from the standard meridian along those parallels. As the term pseudoazimuthal is currently used with a different meaning, Werner's projection is also termed pseudoconic.
In a polyconic projection, one starts directly from the standard meridian. Scale along the standard meridian is uniform. Parallels radiate from the standard meridian, each one with the same radius as it would have as the standard parallel of a conic projection. Scale along the parallels is not necessarily uniform, and how it varies determines which polyconic projection is in use.
This, of course, is my strict definition of a polyconic projection, which firmly excludes conventional projections.
Also, I think it is useful, even among the leftovers, to distinguish between the geometrically-based conventional projections, and the newer ones which are based on more general coordinate mathematics.