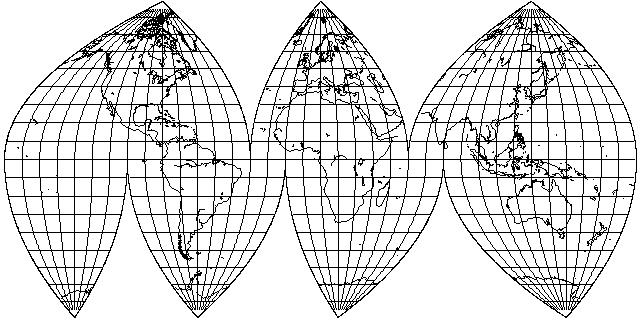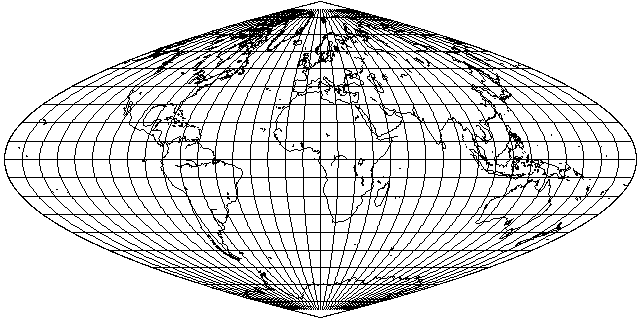
In an attempt to produce a map projection which, like the Mollweide, moderated the extreme shear of the Sinusoidal projection, Lieutenant-Colonel J. E. E. Craster devised an equal-area projection with parabolas instead of sinusoids as its boundaries.
This meant that the height of the parallels was much simpler to calculate than for the Mollweide: it was simply equal to 180 degrees times the sine of one-third of the latitude.
As with the Mollweide, leaving the projection as twice as wide as it is tall meant that areas on the equator were stretched vertically, since the area under a parabola is not the same as the area under a sinusoid; here, the standard parallels are at about 36 degrees and 46 minutes North and South latitude.
This projection has the following appearance:

As it offers only limited benefits over the Sinusoidal, as far as I know, it never became very popular, but I mention it here chiefly because of its relation to the Dietrich-Kitada projection.
It is also known as the Putniņš P4 Projection.
Like other pseudocylindrical projections, it can be interrupted: