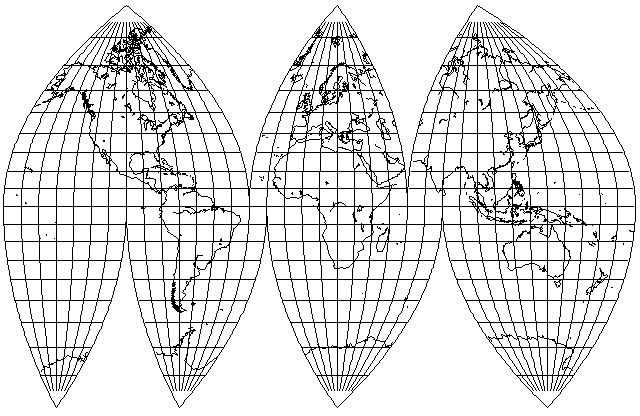
Cylindrical projections have parallels and meridians that are straight lines in the conventional case. A pseudocylindrical projection is still partly based on the idea of wrapping the map around the sphere, because the parallels are straight lines, but it doesn't follow that principle strictly.
Instead, while the scale along each parallel is constant, the scale differs between different parallels.
Thus, while a cylindrical projection might have minimum distortion along the Equator, a pseudocylindrical projection tends to have the opposite orientation, favoring its central meridian.
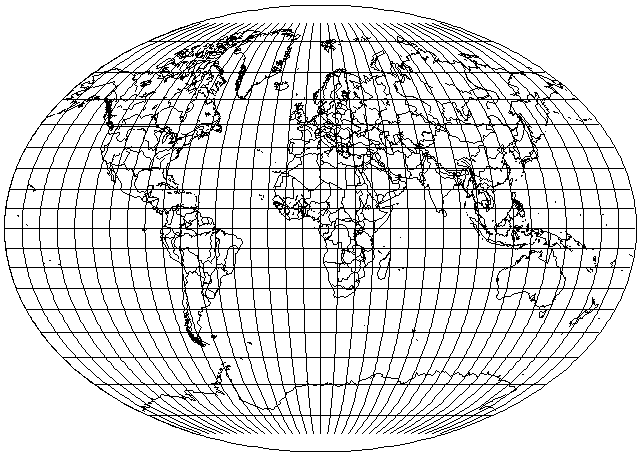
Most pseudocylindrical projections are equal-area, as this type of projection lends itself to providing that property, but this is not always the case. For example, while the equal-area Eckert IV projection is shown here, one can also simply space the parallels of latidude equally instead, obtaining the Eckert III projection.
As another example, here is a pseudocylindrical projection where the central meridian is scaled to match that of the equatorial case of the stereographic projection, in the same way that Adams' equal-area projection matches Lambert's azimuthal equal-area projection.

One of the few examples of a pseudocylindrical projection that is not equal-area that I have seen in actual use is the Modified Gall projection found in the Oxford atlas. In this projection, only a slight narrowing of the parallels as one goes northwards is imposed on the original Gall projection, a cylindrical projection. This projection was devised by Guy Bomford. Another projection of this type was devised by Bartholemew, and is known as the Times projection.
Several computer programs claim to implement the Bomford Modified Gall projection; however, the projection they draw shows almost no deviation from the cylindrical within 30 degrees of the Equator; the one I have seen in Oxford atlases, while it shows only a small deviation in that range, still has meridians that are definitely curved rather than appearing almost flat. The following illustration shows what I think the Modified Gall projection looked like:
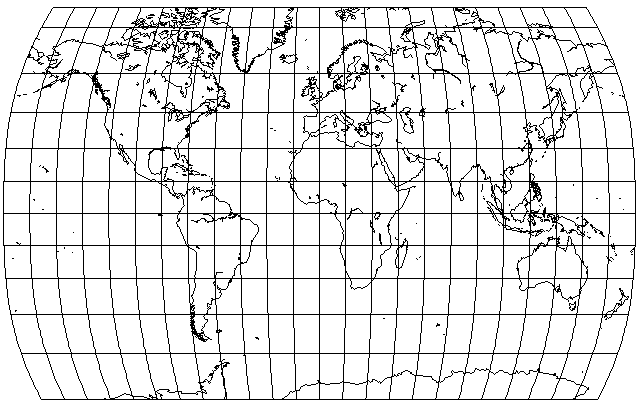
Basically, instead of the horizontal scaling factor being 1 minus a term in the fourth power of the latitude, I also subtract a small term in the second power of the latitude to insure a small, but noticeable, curvature near the Equator. This is now based on a revised formula as I have now had the opportunity to make measurements on an example of the projection in an Oxford atlas.
The formulas used by most map drawing programs for both Guy Bomford's Modified Gall projection and the Denoyer Semi-Elliptical projection were due to John P. Snyder. In his book Flattening the Earth, he mentions that projection in passing, noting that the scale of longitude is "about 1 - 0.4 * phi^4" where phi represents the latitude, compared to that of the equator, so he may merely have been attempting to sketch out roughly what the projection was like, not to seriously propose a method of drawing it. I haven't tried for an exact match myself; as noted above, I added a small term proportional to the square of the latitude to correct the visibly obvious deficiency of implementations of this formula. Scaled to a latitude in radians, my formula becomes 1 - .01857755 * phi^2 - .030077 * phi^4. I calculated it based on matching two of my measurements that seemed most representative, then checking that the overall result had roughly the same appearance as the real map.
Another example of a pseudocylindrical projection that is not equal-area is the Loximuthal projection, here illustrated with its center at 10 degrees east longitude on the Equator:
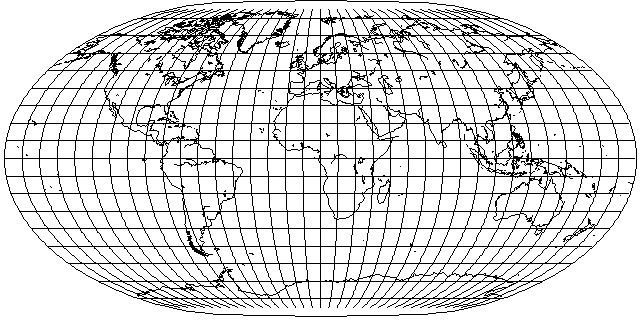
This projection shows every point on the map in its true compass direction from the center of the projection, but without the large size distortion of the Mercator projection. This is done by projecting a Mercator projection down onto equally spaced parallels, as shown in this diagram:
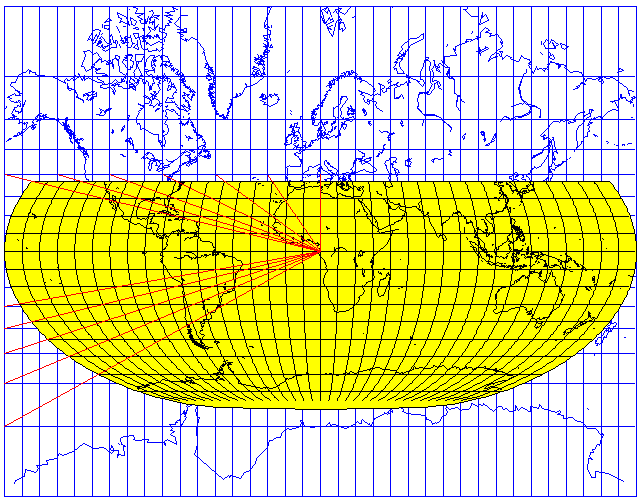
This loximuthal projection is centered on 53.5 degrees North latitude and 113.5 degrees West longitude. Note that the standard parallel is not the widest one; this makes it too complicated for a simplistic program like mine to allow interruptions in this projection, despite the fact that the projection is pseudocylindrical.
A pseudoconic projection is analogous to a pseudocylindrical projection; here, the parallels are concentric arcs. Werner's projection could be termed a pseudoazimuthal projection, since the North pole is its point of origin, but usually the term pseudoazimuthal is used for a completely different class of special-purpose projections.
Another pseudocylindrical projection that is not equal-area is the Fahey projection: