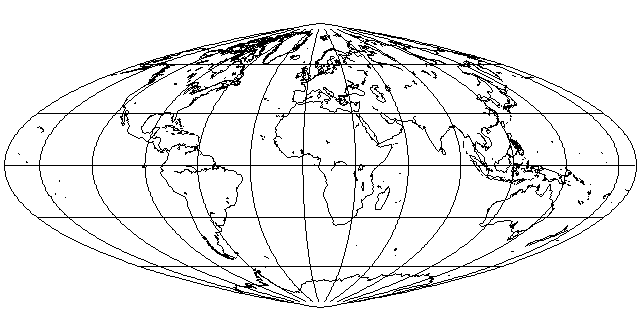
Also known as Adams' Equivalent Pseudocylindrical Projection, this pseudocylindrical projection is also gentler than the Sinusoidal, although it does come to a point at the poles:

However, its main claim to fame is not simply any characteristics it may have as a projection in itself. Instead, this projection works well in combination with other projections.
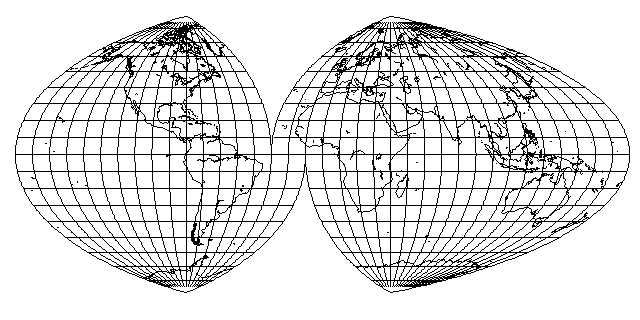
Of course, it can be interrupted, like other pseudocylindrical projections. Note that I have chosen to have the same standard meridians in the northern and southern hemispheres. This projection is designed so that the positions of the parallels are the same as those in the equatorial case of Lambert's Azimuthal Equal-Area projection.
That means that the interrupted projection can be cut at the standard parallels it uses, and either part of a hemisphere on Lambert's projection or part of the world on the Hammer-Aitoff projection can be joined to it, as shown below:
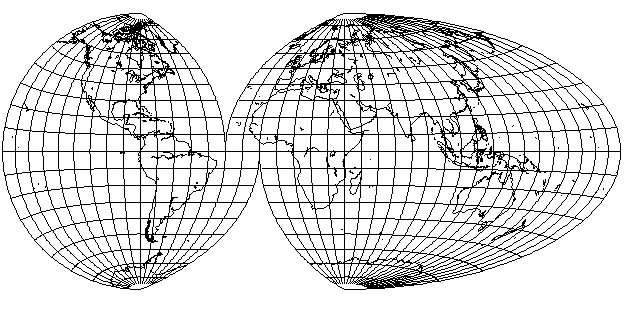
which produces an effect somewhat similar to that of the Oxford projection, although this projection is completely equal-area, whereas notes in the Oxford atlases where I saw that projection stated that it was only approximately equal area.
Incidentally, I've learned that this projection is somewhat obscure. I have found where I likely saw it originally described: on page 207 in the 5th Edition (1944) of Elements of Map Projection with Applications to Map and Chart Construction by Charles H. Deetz and Oscar S. Adams. (The word "Projection" was in the singular on the 4th and 5th editions, but in the plural on the 1st edition.)
As it was actually used, the Oxford projection looked something like this:
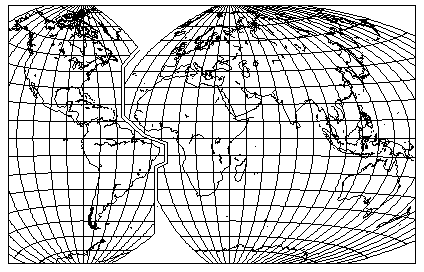
thus, it showed the major continental areas very efficiently, with a chunk of the Atlantic Ocean (and, for that matter, much of the Pacific) omitted.
Both the Oxford projection, used for statistical and economic maps in the back of their atlases starting in 1951, and the Modified Gall projection which they often used for a map of world time zones, were devised by one Brigadier Guy Bomford, who was well-known for his accomplishments in geodesy.