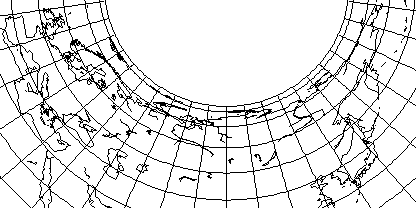
Although Albers' projection is usually used with two standard parallels, it can be used with one, and so used it is still distinct from Lambert's Equal-Area Conic projection, which always gives the pole as a point (and is therefore simply the polar case of Lambert's Azimuthal Equal-Area, with angles around the pole decreased by a constant factor).
Here is an example with a standard parallel of 55 degrees North latitude, suitable for a map of Russia:

and from this, one notes both that this projection shows its relationship to the Cylindrical Equal-Area Projection, and that with so much horizontal stretching present except at the standard parallel, it is not surprising that this projection is usually used with two.
However, if one looks at this map of South America,
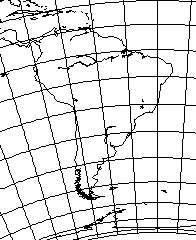
with standard parallel 20 degrees South latitude, it looks surprisingly good for an area with such a large extent of latitude. Thus, it really is only very near the poles that this projection runs into trouble.
Incidentally, for this projection, the radius on which a parallel is drawn is proportional to:
___________________________________________________________
/ 1
/ ( ----------------- + sin(lat_sp) ) - sin(lat)
\/ 2 * tan(lat_sp)
where lat or theta is the latitude, and lat_sp or theta sub s is the latitude of the standard parallel.
Since the area of a circle is proportional to the square of its radius, and since from the Cylindrical Equal-Area projection, we know that the area north of a parallel of latitude is equal to 1 - sin(lat), an expression of this sort is reasonable: the constant from which sin(lat) is subtracted, however, must be chosen so that conformality is obtained at the standard parallel when the longitude is multiplied by sin(lat_sp) as is usual for conic projections.
Attempting to derive a formula from three different books on map projections produced incorrect results, as did my first two attempts to work out the formula on my own, hence exhibiting this result seems worthwhile.