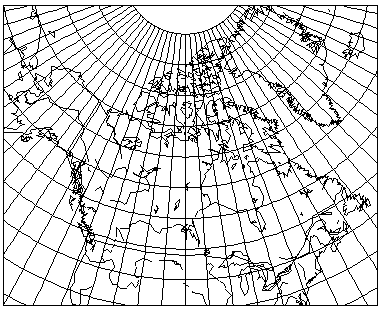
The simple conic projection was once a very popular projection in atlases, particularly for maps of countries like Canada:

as this map shows, having a standard parallel of 55 degrees North latitude, appropriate at least for the most populated portions of Canada.
As the diagram below illustrates:
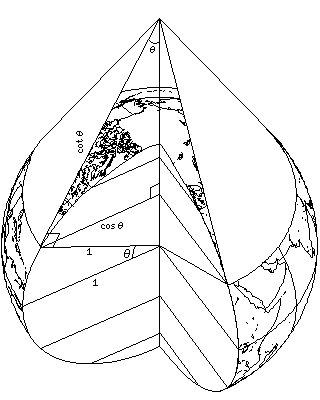
the cone contacting the standard parallel, when flattened to a sheet of paper, contains the standard parallel as an arc with radius cot(lat_sp), which is cos(lat_sp)/sin(lat_sp). Meanwhile, the standard parallel itself on the globe has radius cos(lat_sp), and its scale is true on the projection.
Hence, on a conic projection, the meridians project out from the center of curvature of the parallels at angles equal to the longitude multiplied by sin(lat_sp). Each parallel in the simple conic is a circle with radius cot(lat_sp)+(lat-lat_sp), where lat and lat_sp are expressed in radians.
Unlike the conic conformal, when this projection has two standard parallels instead of one, that does change the appearance of the projection, leading to areas between the two parallels being stretched.
So, given lat_sp1 and lat_sp2, where lat_sp1 is higher, the radius of the standard parallel at lat_sp1 is defined by
cos(lat_sp1)
----------------------------- * (lat_sp1 - lat_sp2)
cos(lat_sp2) - cos(lat_sp1)
and angles from the center of the parallels are reduced by a factor of cos(lat_sp1), the radius of that parallel over the globe, divided by this radius.
Here is another map of Canada, this time drawn with standard parallels at 50 degrees North and 65 degrees North, for comparison:
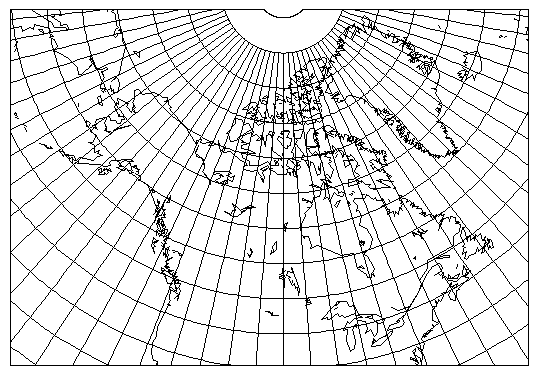
The dimple at the top of the map is the North Pole; it would be invalid to show places north of the North Pole on the map, as they don't exist.