As we saw in the previous section, a modification of the Polyconic was made to improve its perceived suitability for large-scale topographic maps, by causing the meridians to intersect the parallels at right angles.
At the standard parallel, the scale is the same as that on the (simple) Polyconic projection. But the scale on the meridians is not true as they cross the standard parallel. Since conformality is favored on large-scale maps, Captain G. T. McCaw of the Royal Engineers devised, in 1921, a further modification of the Rectangular Polyconic that had an increasing scale on the standard parallel, going away from the standard meridian, so that the projection would at least be conformal on that parallel. (Like the Polyconic and the Rectangular Polyconic, the projection is also conformal at the standard meridian.)
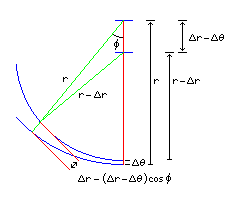
As this diagram illustrates:

for the Rectangular Polyconic, a small displacement in latitude d(lat) which results in the radius of the arcs of the parallels changing by an amount d(radius) leads to a separation between the arcs of
(1 - cos(phi)) d(radius) + cos(phi) d(lat)
where the latitude and phi are finite angles, but the displacements are assumed to be extremely small, so the two green lines of lengths r and r - d(r) can be treated as though they are parallel.
Given that in the Polyconic (and the Rectangular Polyconic) the radius is equal to the cotangent of the latitude, and the derivative of the cotangent is one over the square of the sine, this means that the transverse scale at an angle phi along a parallel is:
1 - cos(phi)
--------------- + cos(phi)
2
( sin(lat) )
To make it more obvious that when phi is zero, and cos(phi) is one, the scale is one, the equation could be rewritten to make it a function of 1 - cos(phi) as follows:
1
( --------------- - 1 ) ( 1 - cos(phi) ) + 1
2
( sin(lat) )
However, for a constant latitude, as a function of phi, it is more convenient to express it as:
1 1
( 1 - --------------- ) cos(phi) + ---------------
2 2
( sin(lat) ) ( sin(lat) )
a simple linear function of the cosine of the angle.
To determine the relationship between phi and the longitude, one uses the same technique as was used for the Mercator projection, of taking the integral of the scale. But in this case, we only know the scale as a function of phi, not of the longitude, so instead of phi being the integral of the scale as a function of longitude, the longitude will be the integral of the reciprocal of the scale as a function of phi.
This integral has an unusual behavior. For latitude 45 degrees, the integral gives:
phi
long = 2 tan( --- )
2
For latitudes greater than 45 degrees, the integral gives:
_____________________
2 phi / 2
long = ----------------------------- * atan( tan( --- ) * / --------------- - 1 )
_____________________ 2 / 2
/ 2 \/ ( sin(lat) )
/ --------------- - 1
/ 2
\/ ( sin(lat) )
and for latitudes less than 45 degrees, the integral gives:
/ / _____________________ \ \
/ | / 2 | \
| | phi / 1 - --------------- | |
| | tan ( --- ) * / 2 | + 1 |
1 | \ 2 \/ ( sin(lat) ) / |
long = ---------------------------- * ln | ----------------------------------------------------- |
_____________________ | / _____________________ \ |
/ 2 | | / 2 | |
/ 1 - --------------- | | phi / 1 - --------------- | |
/ 2 \ | tan ( --- ) * / 2 | - 1 /
\/ ( sin(lat) ) \ \ 2 \/ ( sin(lat) ) / /
At the equator, one instead looks at the scale as a function of x, since the radius is infinite and phi is always zero. Using the Taylor series for the trigonometric functions, the vertical scale works out to be 1 + (x ^ 2)/2, and so, when we integrate, the function turns out to be:
___ x
long = \/ 2 * atan ( ----- )
___
\/ 2
Thus, to find phi or x as a function of longitude, we proceed as follows:
For latitude zero,
x = sqrt(2) * tan( sqrt(2) * long )
For latitude 45,
phi = 2 * atan( 2 * long )
For latitudes greater than 45 degrees,
t1 = sin(lat) t2 = sqrt( ( 2 / t1*t1 ) - 1 ) phi = 2 * atan( tan( ( t2 * long ) / 2 ) / t2 )
For latitudes less than 45 degrees, since
x + 1
if y = -------
x - 1
then xy - y = x + 1
then xy - x = y + 1
y + 1
hence x = -------
y - 1
despite initial appearances, the integral above does have an analytic inverse, and phi can be found as a function of long as follows:
t1 = sin(lat) t2 = sqrt( 1 - ( 2 / t1*t1 ) ) u = 2.71828 ^ ( t2 * long ) v = ( u + 1 ) / ( u - 1 ) phi = 2 * atan( v / t1 )