As you may remember, as one of the steps it took to establish a futuristic atmosphere, the television show Star Trek occasionally showed crewmembers relaxing by playing a form of three-dimensional chess.
Recently, I had turned my attention to the game of Ploy, from the series of Bookshelf Games by 3M. The artwork on the box, and even the dark purple color of the gameboard, convey the idea that this game, although fundamentally an abstract strategy game, still is presented with a futuristic battle between rival fleets of spaceships as its theme.
While a computer simulation, even without a holographic or other three-dimensional display, is probably far better suited to a game involving spaceships maneuvering in three dimensions, I had thought it worthwhile to turn my attention to what might be done in the form of a somewhat elaborate boardgame to allow spaceships to move on a three-dimensional board, and to have definite orientations in three dimensions as well.
One simple possiblity would be to put a model spaceship in the center of a clear plastic cube. This would allow it to be turned to face in six directions, and to be rotated to four orientations around its forwards axis.
If one wishes to admit of allowing a spaceship to be turned to face in a diagonal direction, however, placing a model spaceship inside a clear plastic 26-sided small rhombicuboctahedron doesn't quite properly define the range of orientations one might wish to allow.
While a hexagonal board can be extended to three dimensions, the result also doesn't lend itself well to offering a selection of three-dimensional rotations.
I strongly suspect that someone has already patented the idea which finally occurred to me: have game pieces which consist of two parts.
In fact, something considerably more advanced than what I am proposing, being more general, and applicable to a miniatures game rather than a board game, exists, and is known as the Englobe System, and is currently available, I see. Model spaceships in plastic spheres rest upon stands, and the stands are of variable height so that multiple boards are not needed for three-dimensional space combat.
One part would be a piece in the shape of a spaceship. Perhaps the spaceships in the game might move only forwards, but there would be an indication on the spaceship of in which directions it has ray-guns mounted to fire on enemy ships. Thus, the spaceships might differ in the directions in which they can capture by firing a weapon at a spaceship in an adjoining space, and in the number of spaces they can move in a turn.
The piece would have a round peg extending from the bottom of it, and that peg would be keyed by having a protruding line which could be in the forwards direction. The peg might also be weighted at its base, or long enough in length to ensure the piece can remain securely in the other part of the piece.
The other part would be a small rhombicuboctahedron raised by a column above a square base. The orientation of the square base would be fixed, except for 90-degree rotations with respect to which the part is completely symmetrical, relative to the square spaces on each level of the three-dimensional board.
The small rhombicuboctahedron would have holes in its faces into which the peg on the other part of the piece would be put, and these holes would be surrounded by slots which would match the key on the peg to allow exactly the desired orientations of the spaceship to be indicated. The spaceship portion would be placed on the base portion of the compound piece either horizontally, or from above, including at an angle to the vertical, never from below, so that it would not fall out; the firing patterns of the spaceships would be symmetrical with respect to up and down (in addition to port and starboard) so that this would not be a limitation.
The arrangement would look something like this:

The holes in the five square faces, other than the bottom face, which correspond to the faces of a cube would have eight slots around them, permitting the spaceship to be placed in any orientation involving a rotation that is a multiple of 45 degrees.
Of the twelve square faces which correspond to the faces of a rhombic dodecahedron, the four of them around the equator of the small rhombicuboctahedron and the four which slope up towards the top face would have holes in them; these would have four slots around them in the four cardinal directions, and an additional four slots for diagonal orientations. Assuming that the key on the spaceship is, as illustrated, on its front (the back would also serve) the diagonal ones would point to the corners of a stretched rectangle, where the sides of length one would face the adjoining squares, and the sides of the length of the square root of two would face the adjoining triangles.
For all of the orientations these holes, and the slots around them, would permit for the spaceship, it would be possible to map each of the 26 adjacent cubical cells of the three-dimensional board to the corresponding directions from the spaceship, even though in some orientations, the directions to the neighboring cells would not quite be the same.
I envisage that there would be holes in the triangular faces as well, with six slots spaced at 60 degree angles in them. Here, the mapping of directions from the spaceship might seem to be more difficult, but the diagram above shows how it might be done; instead of a rotation and then a tilt, the mapping would be obtained from a tilt and then a rotation, essentially.
It is even possible that the spaceship could be allowed to face one of the edge cubes at a 45 degree angle; providing this would require twelve slots equally spaced around the holes in the triangular faces. The sixth example in the diagram above shows the mapping of the directions to the adjacent squares for this type of orientation.
If we ignore the fact that the spaceship is symmetrical with respect to top and bottom, so that we can always place it above or to the side of the small rhombicuboctahedron into which its peg is placed, the system of orientations provided allows the spaceship to face any one of its 26 nearest-neighbor spaces. It can have eight possible orientations when facing the six spaces in orthogonal directions. It can also have eight possible orientations when facing the twelve spaces in singly-diagonal directions. When facing the eight spaces through one of the corners of the cubic cell, there are twelve possible orientations, as that is what is needed to reconcile the symmetry with that axis of a cube with the symmetry of the spaceship. So this equals the number of slots found in the holes on the faces of the small rhombicubioctahedron, and it means there is a total of 240 possible orientations provided for.
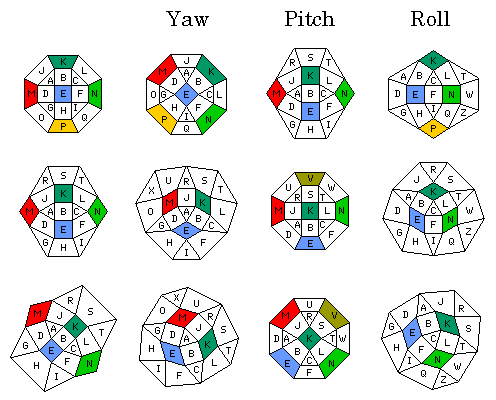
Since the spaceship is shown as facing forwards in a direction perpendicular to the peg which joins it to the small rhombicuboctahedron which serves as a base, it is yaw which will be represented by turning the ship on the peg, while replacing it in the same face of the base. This would be in 45 degree increments on the square faces (although the twelve square faces adjoining two triangles and two squares actually, as noted, really represent eight unequally-spaced orientations), but in 30 degree increments on the triangular faces.
Pitch would usually be represented by moving the spaceship around the base in the direction of its forwards-backwards axis, as though it were in orbit around the small rhombicubioctahedron, and roll would usually be represented by moving the spaceship around the base sideways. However, when the ship is in such an orientation that pitch and roll are in 30 degree, rather than 45 degree, increments, then it is more complicated.
For example, if the ship is facing one of the adjacent cells along a three dimensional diagonal through the corner of the current cell, then roll is in 30 degree increments, and will take the ship on a zig-zag course around the small rhombicubioctahedron which will pass through six of the twelve square faces on edge positions, and through six of the eight triangluar faces.
Thus, it is required that there be twelve slots around the holes in the triangular faces, so that the motions of pitch, roll, and yaw are on an equal footing;
Unlike the possible orientations of a cube, or a dodecahedron, since there are different possible rotations from different starting positions, this set of 240 orientations does not form a group in the mathematical sense, but some partial degree of regularity is present.
Something rather more practical, even though it is oriented towards a greater variety of orientations, as it is aimed at a miniatures game rather than a conventional board game, has been developed by AdAstra Games, and after they used it in games of their own, this unique system led them to become licensed to create Saganami Island Tactical Simulator, a game based on the Honor Harrington novels of David Weber.
Also, there is the Englobe System, in which spaceship models are placed within transparent spheres resting upon stands the height of which is adjustable.
Placing a spaceship model within a transparent cube, as outlined above, and then allowing extra orientations by placing the cube in a molded depression on the gameboard, with a shape like this:
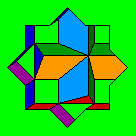
was an idea that occurred to me as a less elaborate way of achieving the same orientations. However, the actual shape of the required indentation to achieve all 240 orientations required for the desired system is more complicated than the one shown. Grooves allowing the cube to rest on an edge are needed in the diagonal as well as the orthogonal directions, and the cube has to be able to rest on a corner as well, but only in four different ways, not eight.
Placing the cube in the hole aligned with the square takes care of the six faces of the small rhombicuboctahedron that are oriented like those of the cube.
The ability to put the cube in a diamond orientation rather than the same orientation as the square, or to lay down one of its sides orthogonally appeared to take care of the twelve faces of the small rhombicuboctahedron that are like those of the rhombic dodecahedron, but on further reflection, this is not true if the diagonal orientations on those faces are included, and so futher thought is required.
Some type of twelve-pointed star would have to be added so that the cube could also be oriented with one of its corners down, in four possible positions, corresponding to the eight triangular faces of the small rhombicuboctahedron which correspond to the faces of the octahedron.
Although placing a spaceship model inside a clear plastic small rhombicuboctahedron was noted above as not defining, by itself, the possible orientations, in comparison to using a clear plastic cube and some sort of guide to obtain the possible orientations of the cube, it seems as though greater simplicity might be achieved. The requirement in the case of the clear plastic small rhombicuboctahedron would be that the players of the game would need to be aware of conventions which describe the permissible orientations of the playing piece.
When it is resting on a square of either kind, that square would have to be aligned with the square space either with its edges running in the four cardinal directions, or with its corners pointing in the four cardinal directions.
When it is resting on a triangle, that triangle would have only four possible orientations, those in which one of the three points on the triangle is pointing towards the middle of one of the four sides of the square space; this permitting 30 degree rotations, the 45 degree rotations which apply when it is resting on a square face would not be allowed, and so the orientations there an apex of the triangle points towards a corner of the square are inadmissible.
The following diagram
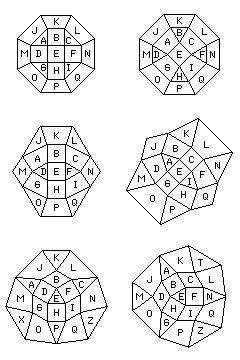
may illustrate how this would work, using the same lettering scheme as in the previous diagram for labelling the adjacent cells, except that in the previous diagram, as the orientation of the spaceship changed, since the diagram of the cells stayed the same, the letters moved, showing directions from the spaceship; here, since we are showing the moving plastic small rhombicuboctahedron around the spaceship, the letters are staying fixed, showing cells.
Upon further reflection, since in this version of the game, the spaceships are carrying the small rhombicuboctahedron with them, the pitch, yaw, and roll circles now always have eight positions instead of twelve. Whether or not this reduces the number of positions from 240 to 208 is unclear; the number of positions may even be increased, since to do this it is necessary to admit the orientations, explicitly excluded above, where the small rhombicuboctahedron is resting on a triangular face, and that triangular face is so directed that one of its points is directed towards a corner of the square. Specifically, symmetry considerations might imply that while the spaceship would face the six cubical faces, and the twelve rhombic dodecahedral faces, in eight orientations, the eight octahedral faces would admit of twenty-four orientations in facing them. But since the clear plastic small rhombicuboctahedron is resting on one of its twenty-six faces on the bottom of the cubical space it is in, and not on the sides of the space, it seems that the simplification from 336 orientations to 208 orientations is forced, and unambiguous as well.
Although one might think that twenty-four orientations of a small rhombicuboctahedron, resting on a triangle, would not be distinct, this diagram shows how two adjacent positions differ:
In the diagram above, again the letters are attached to adjacent cells. The reason for the large difference between the similar orientations is because correspondences between faces of the small rhombicuboctahedron and the adjacent cells are first allocated along the aligned direction of symmetry, which is pointing eastward in one case, and to the northeast in the other.
This chart, where the letters are once again attached to directions from the spaceship, as in the first chart,
illustrating how the pitch, roll, and yaw steps would take place from starting positions facing the three different types of adjacent cell, however, seems to imply that the full 336 orientations will end up being used.
To seriously answer this question, first a means of naming the various orientations is required, so that it won't be necessary to draw hundreds of diagrams.
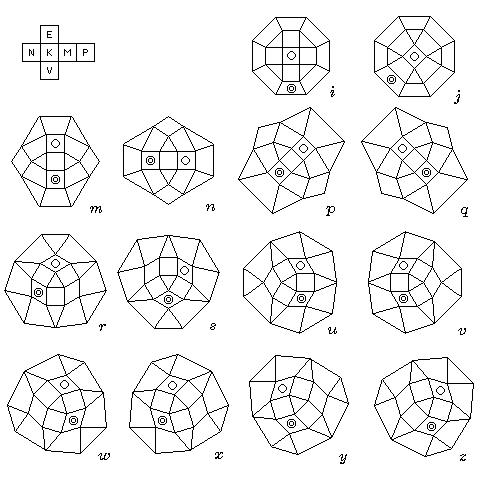
There are fourteen types of orientation of the small rhombicuboctahedron; each of those basic types of orientation corresponds to twenty-four actual orientations, which can be distinguished by placing a cube in relation to the six cubical faces of the small rhombicuboctahedron. So this system of notation includes names for all 336 orientations of interest.
The cube, representing the spaceship model within the clear plastic small rhombicuboctahedron, is labelled on its faces with the letters used above:
K: fore (in front) P: aft (behind) M: port (left) N: starboard (right) E: above V: below
Two of these letters are used to indicate one of the twenty-four possible orientations of the cube; the first shows the face corresponding to the face of the small rhombicuboctahedron marked with one circle, and the second shows the face corresponding to the face of the small rhombicuboctahedron marked with two concentric circles.
The previous chart, showing three orientations, and those which follow from a single step of each of Yaw, Pitch, and Roll from those orientations, can be translated in this notation to:
Yaw Pitch Roll
iEP jEP mKE nNE
mKE sKE iKE rKE
pKE xME jKE zKN
Thus, to see if we want to use all 336 orientations, or, by replacing some of them with near-equivalents, to limit the game to a set of 208 orientations, finding out what happens for longer sequences of yaw, pitch, and roll steps is what is desired.
A table does not need to be too much larger to cover all the fundamentally different cases, since there is a great deal of symmetry here; a complete series of Yaw and Pitch steps from single examples of the two basic orientations for each of the three types of directions should suffice:
iEP Yaw: jEP iEN jEN iEK jEK iEM jEM Pitch: mKE iKE mVE iVE mPV iPV mEP nNE Yaw: uKN nKE uMK nME uPM nPE uNP Pitch: vKE nNK vVK nNV vPV nNP vEP mKE Yaw: sKE mME sME mPE sPE mNE sNE Pitch: iKE mVK iVK mPV iPV mEP iEP rKE Yaw: pKE rME pME rPE mPE rNE pNE Pitch: qKN rVK qVN rPV qPN rEP qEN pKE Yaw: xME pME xPE pPE xNE pNE xKE Pitch: jKE pVK jVK pPV jPV pEP jEP zKN Yaw: qEK zMK qEM zPM qEP zNP qEN Pitch: mKN zVN mVN zPN mPN zEN mEN
The simple transformation of w and z to u, and x and y to v, (or with x going to r, and w also going to r with a suitable change of the cube portion of the notation, and similarly z going to s, and y also going to s with a suitable change of the cube portion of the notation) although obvious enough, will only reduce the number of combinations from 336 to 240. To reduce the number of combinations from 336 to the more appropriate value of 208, so that each of the 26 neighboring cells may be faced in exactly eight ways, corresponding to eight stages of roll, and with the additional benefit that now each endpoint of any yaw, pitch, or roll move also serves as the starting point for any yaw, pitch, or roll move, requires a mapping based on the complete orientation of the playing piece, and in which all fourteen small rhombicuboctahedron orientation types would be used, but each of the last eight only for eight of the possible twenty-four cube values.
Allowed: rKE rKM rKV rKN rPV rPN rPE rPM
-------------------------------
Replaces: xKE xKM xKV xKN xPV xPN xPE xPM
wKN wKE wKM wKV wPN wPE wPM wPV
Allowed: sEK sMK sVK sNK sVP sNP sEP sMP
-------------------------------
Replaces: zEK zMK zVK zNK zVP zNP zEP zMP
yNK yEK yMK yVK yNP yEP yMP yVP
Allowed: uEM uMV uVN uNE uVM uME uEN uNV
-------------------------------
Replaces: zEM zMV zVN zNE zVM zME zEN zNV
wEM wMV wVN wNE wVM wME wEN wNV
Allowed: vEN vME vVM vNV vMV vEM vNE vVN
-------------------------------
Replaces: yEN yME yVM yNV yMV yEM yNE yVN
xEN xME xVM xNV xMV xEM xNE xVN
Allowed: wEK wMK wVK wNK wVP wNP wEP wMP
-------------------------------
Replaces: uEK uMK uVK uNK uVP uNP uEP uMP
rEN rME rVM rNV rVN rNE rEM rMV
Allowed: xEK xMK xVK xNK xVP xNP xEP xMP
-------------------------------
Replaces: vEK vMK vVK vNK vVP vNP vEP vMP
rEK rMK rVK rNK rVP rNP rEP rMP
Allowed: yKE yKM yKV yKN yPV yPN yPE yPM
-------------------------------
Replaces: vKE vKM vKV vKN vPV vPN vPE vPM
sNE sEM sMV sVN sNV sEN sME sVM
Allowed: zKE zKM zKV zKN zPV zPN zPE zPM
-------------------------------
Replaces: uKE uKM uKV uKN uPV uPN uPE uPM
sKE sKM sKV sKN sPV sPN sPE sPM
Note that the first thirty-two of the sixty-four allowed orientations noted above are cases where the spaceship faces the edges, not the corners.
Incidentally, the rule might be that a pitch, yaw, or roll move would bring a piece into the natural one of the 336 possible orientations, and the simplification from 336 to 208 orientations would only take place before the piece is re-oriented again by a pitch, yaw, or roll move.
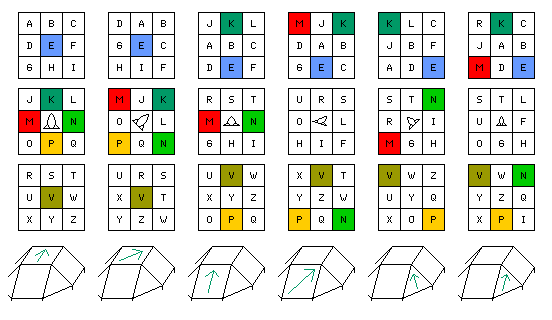
To retreat from all this complexity to a simple, concrete illustration, if the rule of movement noted at the beginning is adopted, wherein spaceships move only forwards, and each move normally consists of three steps, the first being a move in the direction the ship was pointing, the second an opportunity to capture opposing pieces by firing its ray-guns, and the third the chance to maneuver one step in pitch, roll, or yaw for the next move, then the five images below will illustrate an example of a fork.
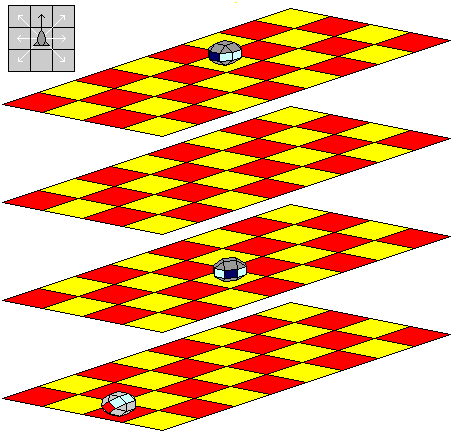
The pieces illustrated are all of the same type. Two pieces belonging to the dark gray side, and one belonging to the light gray side, are illustrated. It is light gray's move.
The pieces move forwards (direction K) and can fire their ray guns in directions J, L, M, N, O and Q.
At the beginning, light gray's spaceship is moving forwards, or North, and is tilted, or rolled, 45 degrees from the vertical towards the West or its own left or portside.
In the form of algebraic notation I will use here, light gray's spaceship is on cell c1a, and the two dark gray spaceships are on cells c4b and b5d.
Using the notation above for orientations, light gray's spaceship is in orientation nNE, and the two dark gray spaceships are in orientations jEN and iEK respectively.
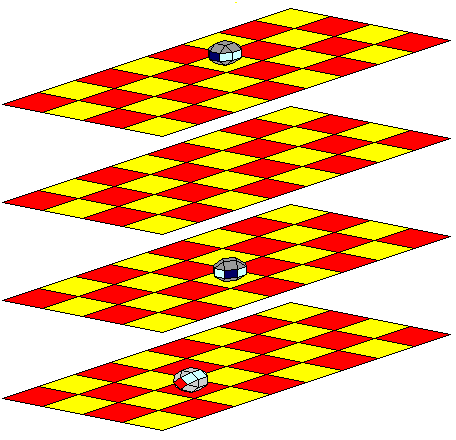
The first part of light gray's first move is to move two spaces forwards, to cell c3a. As there are no pieces to capture by firing at them, (the ship's starboard guns attack cells d2b, d3b, and d4b) no capture stage is present in the move.
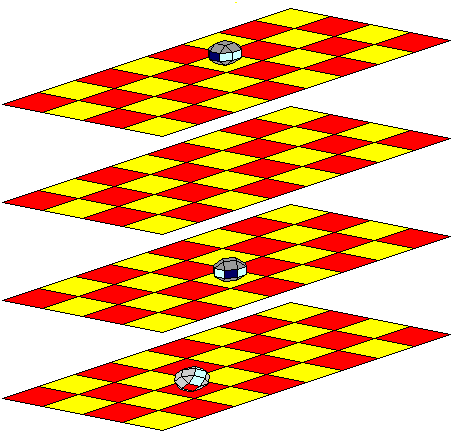
Then, to finish the move, light gray's ship makes a one-step cource change in pitch, turning upwards in its own co-ordinate system.
The orientation of light gray's ship is now vKE (or yKE if simplification to the basic 208 orientations takes place immediately).
This brings its starboard guns to bear on cells d2a, d3b, and c4b, thus threatening the dark gray ship on c4b. (If its orientation were changed to yKE, then its starboard guns would be aimed at d3a, d3b and d4b, and so the example would need to be changed slightly: the dark gray ship on c4b would have to be placed at d3a instead.)
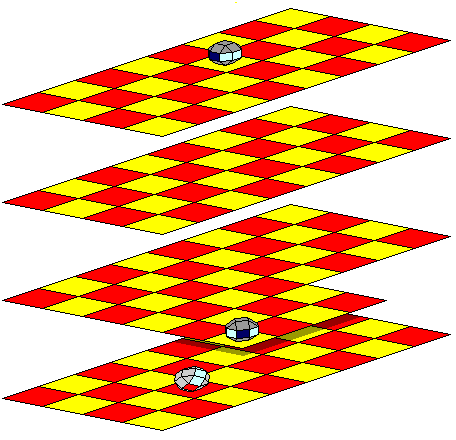
The dark gray ship at c4b therefore moves away to f1b. As it is moving to the edge of the board, it will likely change orientation as well, but this is not shown; let us assume it changes course one step in yaw to be headed East instead of South-East. Note that the board on the second level in this diagram is extended to show its destination.
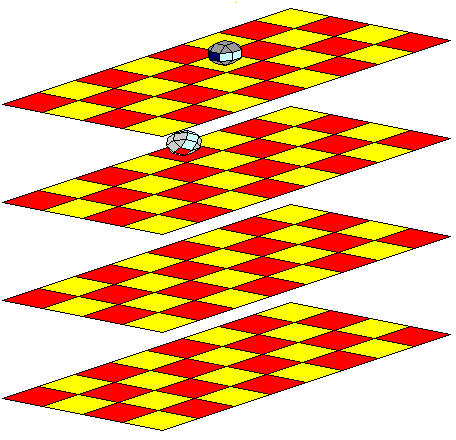
The light gray spaceship then moves to a5c, and there, without further rotation, its guns attack the dark gray piece at b5d, which is therefore captured.
These three moves could be recorded as:
c1a - c3a (vKE) c4b - f1b (iEN) c3a - a5c N x b5d
where the N in the final move shows which ray gun is used to attack the piece at b5d, and any change of orientation in that move is not shown.
Since the pieces are being oriented in three dimensions, the intent is that they will also move in three dimensions. This requires a three-dimensional board.
A three-dimensional board composed of multiple two-dimensional boards stacked one on top of another, suspended with perhaps two inches (5 cm) of separation between them makes it difficult to reach interior positions of the board.
AdAstra Games, mentioned above, uses a two-dimensional board for its games Attack Vector: Tactical and Saganami Island Tactical Simulator, and represents the vertical position of a spaceship by piling plastic squares under it to elevate it. This is reasonable on a large, uncrowded, board, but it seems to me better suited to a miniatures game (such as those are) than to a chess game.
An intermediate solution, suited to a playing field as large as 12 by 12 by 12, has occurred to me:
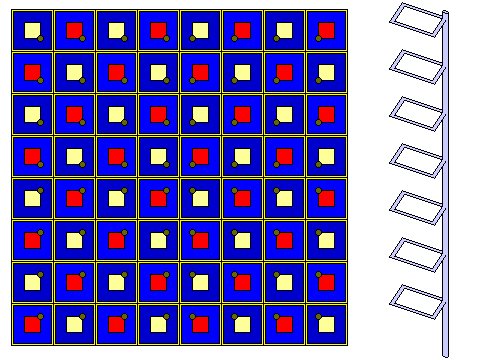
A vertical supporting member can hold a stack of individual squares, and be inserted into a two-dimensional base with a hole on the corner of each square, with space between the squares.
The elevated squares might be made of transparent material, and it might still be necessary to use perhaps right-angled tweezers (or simply to temporarily remove the relevant stack of squares from the base board) to move pieces in interior locations.
Note that the holes in the baseboard are oriented so that the supporting pillars for the stacks of elevated squares are positioned towards the center of the board.
Of course, this design may well have been tried, and failed on the grounds that it rattled too much.