Wargames are among the most complicated board games in existence; proposing to make them more complicated would, therefore, seem insane: but my intent is to make them simpler by making them more complicated.
Almost all wargames (of the kind that use game boards divided into spaces, as opposed to the kind that use miniatures) use a board divided into hexagonal spaces.
This, besides being unfamiliar, makes it difficult to make moves correspond to the points of the compass.
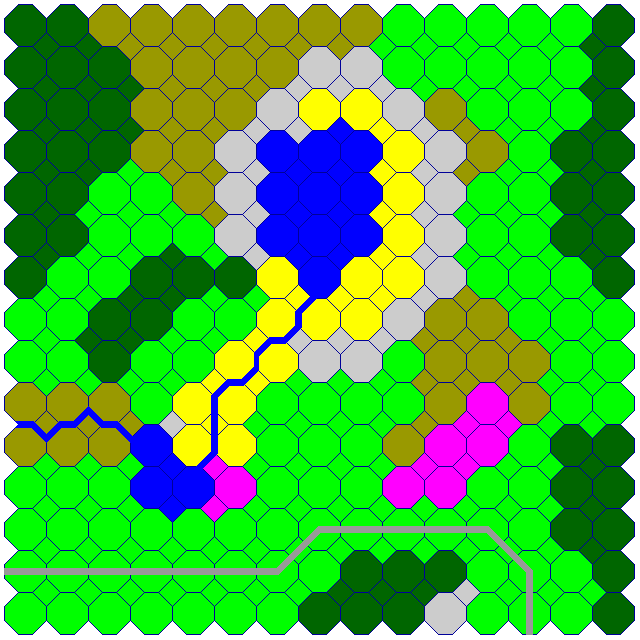
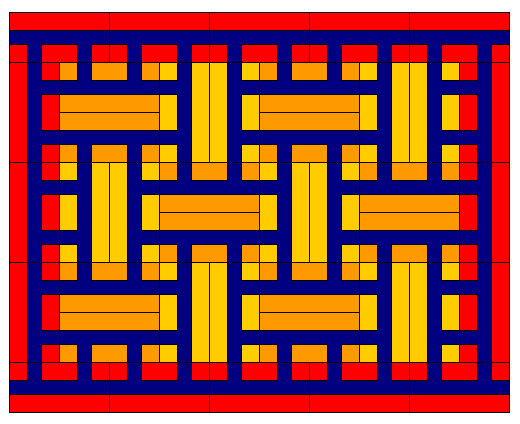
I propose an alternative board design. I don't really think I'm the first to come up with this, though; I think the idea has been used in RPGs on occasion. What I advocate is using a board that looks like this:

The idea is that all moves begin and end on octagonal spaces, but in addition to orthogonal moves, diagonal moves are also possible. The movement cost of a move would be the total of:
1 x the Terrain Factor of the starting octagon 1 x the Terrain Factor of the ending octagon 2 x the Terrain Factor of any octagon passed through 1 x the Terrain Factor of any square passed through
The underlying logic behind this rule might be made clearer by looking at this diagram:

Now, all moves begin and end on white circles; moving from one circle to another, whether white or red, along a line counts as one step, and that step is multiplied by the Terrain Factor for the terrain type in which that line is located.
So moving from one octagon to an adjacent one, if all Terrain Factors involved are unity, requires 2 movement points, and a diagonal move requires 3 movement points. Thus, the design is based on using 1.5 as a crude approximation of the square root of 2.
Also note that the stream shown in the diagram is not navigable, and thus functions only as a barrier. A river that can be used for movement by boat would enter and leave the octagons in the same way as the road shown in the bottom of the diagram instead of the way the stream does.
This principle could also be generalized, to use 2.25 as an approximation to the square root of 5, as shown below:
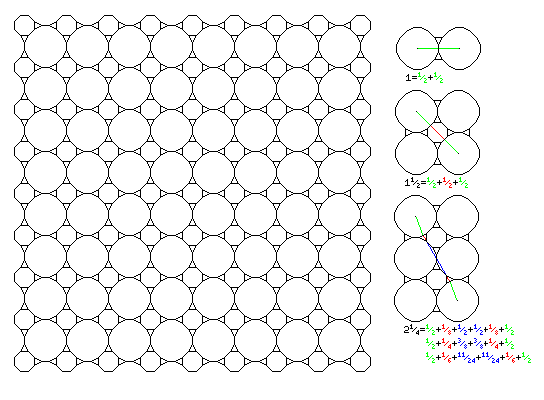
allowing movement in 16 directions, instead of just 8 directions, to take place at approximately equal speeds.
I was inspired by the line-drawing keys of the Culler-Fried keyboard to do this; as you can see from the diagram, I'm not sure what is the ideal portion of movement to assign to each space on the map for the purpose of combining Terrain Factors for the additional directions.
Attempting to use designs like this:
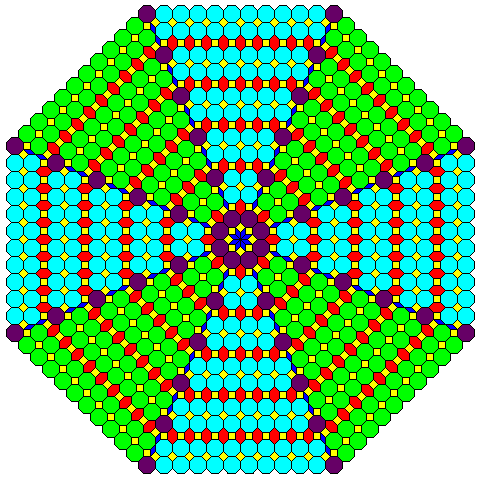
to achieve true octagonal symmetry, perhaps following the Keplerian octagonal tilings described elsewhere, or even the Ammann-Beenker tiling, might lead to a gameboard whose connections follow this type of pattern, if the shapes other than the small squares and the octagons are not used:

If I allow myself to cheat a bit, and flatten the octagons slightly in the direction towards the center, I can, although with only infrequent contact between the eight segments of the board, have each segment composed of a simple pattern of alternating octagons and squares:

In the center region, I cease to follow the pattern consistently, in order to allow the center region to be part of the game: it could be the goal the players are racing toward, perhaps with mountain climbing as the theme of the game.
Something much simpler, however, might be the best way to achieve a close approximation to the ability to move at an equal speed in any direction.
Using a simple square grid, but with each square divided into smaller units, a normal orthogonal move can be three steps, and a normal diagonal move two steps, with all possible combinations of those moves being available.
An approximation to a circular range of movement can be achieved by making the maximum distance of a single move equal to the square root of 10. In this way, an orthogonal move (distance: 3) can receive an optional bonus orthogonal move to the side, while a diagonal move (distance: 2.86) receives a larger optional bonus diagonal move to the side, both working out to the same move in an alternate direction (distance 3.16),
Another possibility is illustrated below:

Here, areas with a hexagonal grid alternate with areas with the octagonal grid, both types of areas having two orientations, with the intent that imperfections in each type of grid will be averaged out.
Another thing in most wargames that could be simplified by being made more complicated, in my opinion, is the Combat Results Table.
This table shows what happens for different die rolls based on the ratio of the forces of the attacker and the defender; it may look like this:
1:3 1:2 1:1 2:1 3:1
1 AE AE AE EX EX
2 AE AE AE EX EX
3 AE AE EX EX EX
4 AE EX EX EX EX
5 EX EX EX EX DE
6 EX EX DE DE DE
It has two problems. One is that one has to remember to round off this ratio in favor of the defender. Another is that sometimes improbable results appear in the table in order that the battles not be without risk for either side.
So how I would improve the typical CRT is by making it larger.
Instead of rolling one die to resolve combat, I would use the total of three dice, allowing a distribution of results approximating the normal distribution, and allowing improbable results to be possible but unlikely.
Instead of having columns, each one headed with a particular ratio, I would have additional columns between each pair of exact ratios; if the ratio is between 1:3 and 1:2, one looks in the column between the 1:3 column and the 1:2 column.
Thus, one would obtain tables that look like this:
1:4 1:3 1:2 1:1 2:1 3:1 4:1 5:1 6:1
3 AE AE AE AE AE AE AE AE AE AE AE AE AE AE AR AR AR AR AT
4 AE AE AE AE AE AE AE AE AE AE AE AR AR AR AR AR AT AT XD
5 AE AE AE AE AE AE AE AE AE AR AR AR AR AT AT AT XD XD EX
6 AE AE AE AE AE AE AE AE AR AR AT AT AT XD XD XD EX EX EX
7 AE AE AE AE AE AE AE AR AT AT XD XD XD EX EX EX EX EX XH
8 AE AE AE AE AE AE AR AEDH EX EX EX EX EX EX EX S S XH DR
9 AE AE AE AE AE AE AR AEDH EX EX EX EX EX EX S HX XH DR DR
10 AE AE AE AE AE AR XH HX EX EX EX EX EX S HX XH DR DR DR
11 AE AE AE AE AE AR HX S EX EX EX EX S HX XH DR DR DR DR
12 AE AE AE AE AR XH S EX EX EX S S HX XH DR DR DR DR DE
13 AE AE AE AE AR HX S EX S S S HX XH DR DR DR DR DE DE
14 AE AE AE AR XH S EX EX S S HX XH DR DR DR DR DE DE DE
15 AE AE AE AR HX EX EX S S HX XH DR DR DR DR DE DE DE DE
16 AE AE AR XH S EX EX HX HX XH DR DR DR DR DE DE DE DE DE
17 AE AE AR HX EX EX AT DEAH XH DR DR DR DE DE DE DE DE DE DE
18 AE AR EX EX EX AT AT DR DR DR DE DE DE DE DE DE DE DE DE
AE: Attacker Eliminated
AR: Attacker Retreats
DR: Defender Retreats
DE: Defender Eliminated
XH: Exchange Half (weaker side eliminated; inflicts casualties half its own size on stronger side)
EX: Exchange
XD: Exchange Double (weaker side eliminated; inflicts casualties twice its own size on stronger side)
AT: Attrit (weaker side unscathed; inflicts casualties its own size on stronger side)
HX: Half Exchange (both sides suffer casualties equal to half the size of the weaker side)
S: Spent (combat ends for both units for the turn without casualties)
AEDH: Attacker Eliminated, Defender Halved
DEAH: Defender Eliminated, Attacker Halved
Occasionally, there have been games which allow one to build the game board one tile at a time. Tiles might be hexagonal, square, or rectangular.
Often, this is made complicated by the need to avoid dead ends.
Here is a simple and uniform scheme that might be useful.
A single type of rectangular tile is used, a card that is twice as high as it is wide. Each card has entrances or exits in four fixed locations.
There would be different types of card.
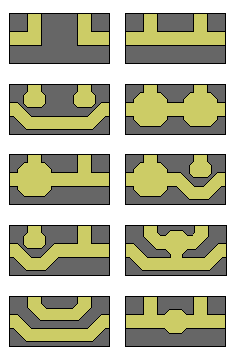
Each card would represent a portion of the dungeon, with passages connecting some of the exits to each other, and there might be one or two chambers, represented by enlarged circular areas, present as well. When a card is placed on the layout, any chambers might be marked with tokens to indicate they are not visited, and when one is entered, a card from an encounter deck could be drawn to determine if a monster, a trap, or a treasure is present.
A turn in such a game might work like this:
At the start of a turn, one may be standing at one of the exits from a card, or one of the four entrances to the dungeon. If a card is not present beyond that point, one is drawn from the dungeon deck, and placed in the position where you are about to enter. A possible result of the first few moves of one player is illustrated in the diagram below:
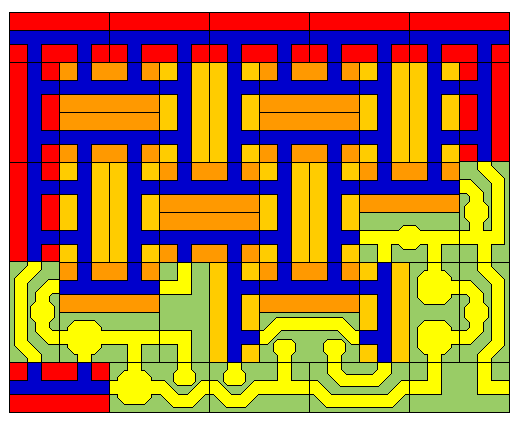
(Note that it is also possible, in the case where one is entering the location of the first of two cards forming one of the alternate orange and reddish-orange squares within the dungeon, that one might flip a coin to determine if the orientation shown on the board or the opposite one is used for the two cards, to further randomize the dungeon.)
Then, you can either proceed to a chamber in the area you are proposing to enter, or, without passing through any chambers, proceed to one of the exits of that card through the passages on it.
In addition to proceeding directly to a chamber, one can elect to search; in that case, one loses a turn, but if the encounter in the chamber is a trap, one has an extra chance of avoiding it.
Games with similar mechanics, designed as simplified versions of fantasy role-playing games, already exist, of course.