Some books about music refer to a persistent "myth" that it is possible, using only two keyboards, to construct an instrument on which it is possible to play music in any key using just intonation. Indeed, it is true that it is not possible, with only 24 keys to the octave, to construct an instrument that will play in perfect just intonation in every key.
However, it is possible to exhibit an example of the type of keyboard that has given rise to this "myth", so that its capabilities, as well as its limitations, can be seen. If one is willing to approximate just intonation to the same level as equal temperament with 53 notes to the octave does, respecting differences of the order of the syntonic comma, but neglecting differences of the order of the schisma, one can indeed, with only one alternate pitch for each of the twelve notes in the octave, provide a scale of tones closely corresponding to just intonation with each of the twelve notes in the conventional octave as a possible starting point.
Thus, what may be constructed with 24 keys to the octave is a keyboard which allows playing diatonic music in just intonation in any of the twelve conventionally designated keys, even if nothing can be ensured concerning the pitch of accidentals, and with the provision that one has to make a jump in pitch when one transposes around the far end of the circle of fifths. This will be shown explicitly below.
The most obvious design:
Note: C Db D Eb E F Gb G Ab A Bb B
------------------------------------------------------------
Key:
80 256 32 320 1024 128 1280
Db -- --- -- --- ---- --- ----
81 243 27 243 729 81 729
80 256 32 320 40 128 16
Ab -- --- -- --- -- --- --
81 243 27 243 27 81 9
80 10 32 4 40 128 16
Eb -- -- -- - -- --- --
81 9 27 3 27 81 9
10 32 4 40 5 16
Bb 1 -- -- - -- - --
9 27 3 27 3 9
10 5 4 3 5 16
F 1 -- - - - - --
9 4 3 2 3 9
9 5 4 3 5 15
C 1 - - - - - --
8 4 3 2 3 8
9 5 45 3 27 15
G 1 - - -- - -- --
8 4 32 2 16 8
135 9 81 45 3 27 15
D --- - -- -- - -- --
128 8 64 32 2 16 8
135 9 81 45 405 27 243
A --- - -- -- --- -- ---
128 8 64 32 256 16 128
135 1215 81 729 405 27 243
E --- ---- -- --- --- -- ---
128 1024 64 512 256 16 128
2187 1215 81 729 405 3645 243
B ---- ---- -- --- --- ---- ---
2048 1024 64 512 256 2048 128
------------------------------------------------------------
Note: C C# D D# E F F# G G# A A# B
seems to require three pitches for some of the notes, even to handle only 11 of the possible keys.
However, while 2187/2048 is a full syntonic comma (81/80) higher in pitch than 135/128, 256/243, on the other hand, is only a tenth of a syntonic comma below 135/128. Thus, the two would be represented by the same note on a 53-note scale.
Similarly, 1024/729 is close to 45/32, while 729/512 differs from it by a syntonic comma.
1280/729 and 16/9, on the other hand, differ by a full syntonic comma, while it is 3645/2048 that is redundant.
Thus, it is by maintaining just intonation to the precision of the comma, but ignoring smaller differences (on the order of a schisma) that one can achieve just intonation with a double keyboard in all keys.
Illustrating this in terms, therefore, of the 53-note scale directly, we get:
Note: C Db D Eb E F Gb G Ab A Bb B
-------------------------------------
Db 53 5 14 22 27 36 44
Ab 53 5 14 22 31 36 45
Eb 53 9 14 23 31 36 45
Bb 1 9 14 23 31 40 45
F 1 9 18 23 32 40 45
C 1 10 18 23 32 40 49
G 1 10 18 27 32 41 49
D 5 10 19 27 32 41 49
A 5 10 19 27 36 41 50
E 5 14 19 28 36 41 50
B 6 14 19 28 36 45 50
F# 6 14 23 28 37 45 50
-------------------------------------
C C# D D# E F F# G G# A A# B
Thus, we see how a musical instrument with two keys for each of the twelve notes in the octave can play diatonic music in any of the twelve keys, subject only to the small errors in the 53-note version of equal temperament.
Here is a set of simple integer ratios which offers two possibilities for most, but not all, notes on the scale. It is a scale of relative pitches, like the sequence starting with do, re, mi... for the diatonic major scale, not a sequence of fixed notes.
This sequence is made up of these 22 ratios:
Sa Ri Ga Ma Pa Dha Ni
256 10 32 5 4 45 128 5 16 15
r1 --- R1 -- g1 -- G1 - m1 - M1 -- d1 --- D1 - n1 -- N1 --
243 9 27 4 3 32 3 81 3 9 8
S 1 P -
16 9 6 81 27 64 2 8 27 9 243
r2 -- R2 - g2 - G2 -- m2 -- M2 -- d2 - D2 -- n2 - N2 ---
15 8 5 64 20 45 5 16 5 128
S R1 R2 R3 M1 M2 P D1 D2 D3
Sa Ra Ri Ru Ma Mi Pa Dha Dhi Dhu
G1 G2 G3 N1 N2 N3
Ga Gi Gu Na Ni Nu
Many of them are ratios we saw above, others are simpler ones, since the table above was derived from movement only on the circle of fifths, and thus largely rests on Pythagorean intervals, while these ratios make freer use of the 5:4 major third ratio.
Not all these ratios are accepted by all authorities on Indian music. Thus, another account gives 32/31 as r1 and 31/16 as N2. This scale suggests that the Indian Ragas, specifically the South Indian or Carnatic Ragas, while using notes and intervals often unfamiliar in Western music, are still based on similar underlying harmonic principles.
The bottom section of the table shows how the twelve notes of the scale, excluding microtones, are referred to when tabulating the scales of the different Ragas.
There are other attributes that differ from one Raga to another, but the Ragas have ascending and descending scales associated with them. An individual Raga may only use 5, 6, or 7 notes in each scale, but they can be grouped in families, called Melakartha Ragas, which have a full seven-note ascending scale and a full seven-note descending scale, including one note belonging to each of the seven degrees of the scale, from the four possibilities for each degree except for Sa (the unison) and Pa (the perfect fifth).
These are the basic Ragas from which other Ragas may be derived, and there are exactly 72 of them; the possible combinations (using the notation on the bottom of the table above) are:
S (R1 G1) M1 P (D1 N1)
(R1 G2) M2 (D1 N2)
(R1 G3) (D1 N3)
(R2 G2) (D2 N2)
(R2 G3) (D2 N3)
(R3 G3) (D3 N3)
This, though, does not yet tell us which of the two values for most of the notes is to be chosen to produce consonance.
If we use the notation in the upper part of the chart, and lay out the notes in the two-dimensional diagram with which we began this section, we have:
N2 G2 m2 D2 n2 R2 M1 g2 P N1 d2 S G1 r2 m1 D1 M2 n1 R1 g1 d1 r1
Thus, we have a long Pythagorean stretch of notes separated by fifths, from r1 upwards to N2, and short stretches a major third above and below the center of that stretch.
This short table shows the frequencies of the notes on the scale for the octave starting with middle C:
Equal Hammond Telharmonium C=256 A=435 A=425 Meantone Just C 261.63 261.54 85 104 261.62 320 80 256 258.65 252.71 C 254.21 264 256 277.18 277.07 71 82 277.19 356 84 271.22 274.03 267.73 C# 265.63 D 293.66 293.70 67 73 293.66 440 98 287.35 290.33 283.65 D 284.21 297 288 311.13 311.11 105 108 311.12 352 74 304.44 307.59 300.52 Eb 304.11 E 329.63 329.60 103 100 329.70 494 98 322.54 325.88 318.39 E 317.76 330 320 F 349.23 349.09 84 77 349.20 315 59 341.72 345.26 337.32 F 340 352 341.33 369.99 370 74 64 369.95 362 64 362.04 365.79 357.38 F# 355.27 G 392.00 392 98 80 391.89 725 121 383.57 387.54 378.63 G 380.13 396 384 415.30 415.14 96 74 415.32 508 80 406.37 410.59 401.15 A 440 440 88 64 440 444 66 430.54 435 425 A 425 440 426.67 466.16 466.09 67 46 466.01 456 64 456.14 460.87 450.27 Bb 454.74 B 493.88 493.71 108 70 493.85 672 89 483.26 488.27 477.05 B 475.16 495 480
The first column shows the frequencies of the notes as actually used in the equal-tempered scale at the current concert pitch of A=440 Hz. The second column shows the approximations to those frequencies used in the classic Hammond organ using tonewheels, followed by the number of teeth on the gears that drive the tonewheels, and the third does the same for one of the designs used on the Telharmonium of Thaddeus Cahill. The frequencies used are based on A=440 Hz, to best serve purposes of comparison, but it is possible that the Telharmonium instead used C=256 Hz as its pitch, because the gearing ratio for C is simpler, and because this pitch is cited in the first Telharmonium patent.
The fourth column shows the lower frequencies for the "scientific" scale of pitches. The fifth column shows the frequencies for a standard of A=435 Hz, as this was fixed at one time as an official standard in France, and is occasionally used at the present time for tuning organs. The sixth column shows the frequencies for a standard of A=425 Hz, as this is close to that in use during much of the classical period. The seventh column shows quarter-comma meantone tuning with A=425 Hz; the eighth column shows the just intonation pitches of Helmholtz which gave rise to the exact numerical value of the current concert pitch, and the ninth shows just intonation pitches starting from C=256 Hz.
For more information about the Hammond organ, continue on to this later page in this section.

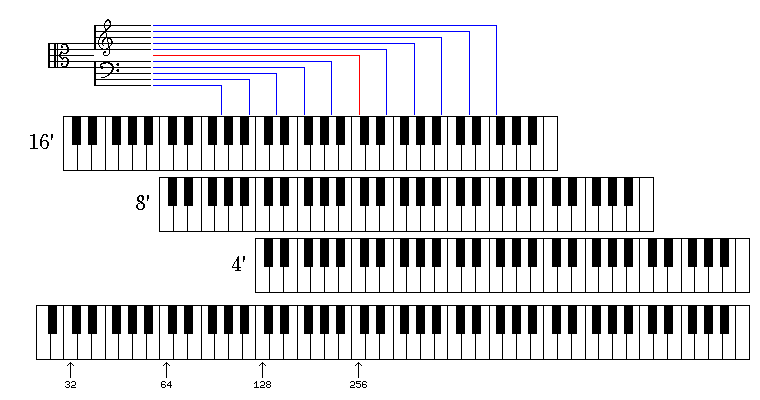
The diagram above shows the relationship of the piano keyboard to the musical staves, as well as showing the relationship of the organ keyboard to them. Although an organ keyboard typically has only 61 keys, through the use of just three stops, the 16-foot, 8-foot, and 4-foot stops, it approximates the piano's compass.
The 8-foot stop is so named because open pipes on a pipe organ (rather than closed; this halves the frequency of the sound produced, lowering the note by an octave) produce a note with a frequency of about 64 cycles per second, or 64 Hertz. Thus, each rank of pipes is named by the length of its longest pipe. Since the length of pipes is proportional to wavelength, it is inversely proportional to frequency. The same relationship, of course, applies to any cylindrical tube with a similar source of oscillations at one end, and so it applies to flutes and recorders when no holes are opened.
This table shows three systems of notation for the notes that belong to different octaves:
(1) (2) (3) CCC C,, C0 16 Hz 32' EEE E,, E0 20 Hz 25 3/5' GGG G,, G0 24 Hz 21 1/3' BBB B,, B0 30 Hz 17 1/15' CC C, C1 32 Hz 16' EE E, E1 40 Hz 12 4/5' GG G, G1 48 Hz 10 2/3' BB B, B1 60 Hz 8 8/15' C C C2 64 Hz 8' E E E2 80 Hz 6 2/5' G G G2 96 Hz 5 1/3' B B B2 120 Hz 4 4/15' c c C3 Tenor c 128 Hz 4' e e E3 160 Hz 3 1/5' g g G3 192 Hz 2 2/3' b b B3 240 Hz 2 2/15' c1 c' C4 Middle c 256 Hz 2' e1 e' E4 320 Hz 1 3/5' g1 g' G4 384 Hz 1 1/3' b1 b' B4 480 Hz 1 1/15' c2 c'' C5 512 Hz 1' c3 c''' C6 1,024 Hz
The system in the column noted by (2) is the Helmholtz pitch notation; that in the column noted by (3) is the Scientific pitch notation. In the first column is one possible form of the English multiple C notation.
Note that for all these systems, the octave begins with C, and not with A, as is the normal convention in music, potentially confusing though it may be.
Moving back to the simple world of the equal-tempered scale, the following image
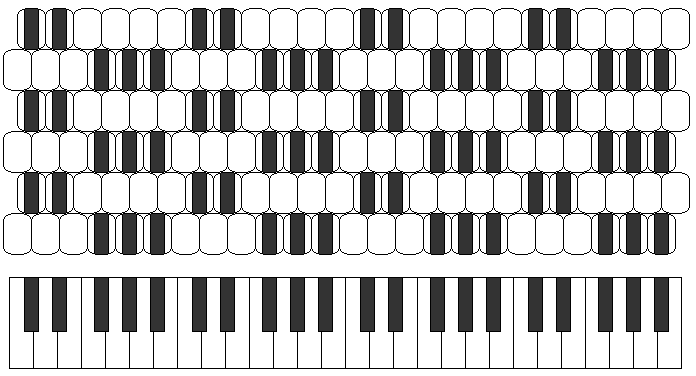
illustrates the Jankó keyboard, in comparison to a conventional piano keyboard on the same scale. (In fact, the spacing of keys on the Jankó keyboard is normally smaller than that of a conventional keyboard, to make it more convenient to play chords.)
The three buttons in a vertical line on the Jankó keyboard are all connected together, so that they can be used to play the same note. On this keyboard, since F is a semitone higher than E, it stands in the same relation to E as D# does to D. This, combined with the repetition of the keyboard arrangement three times over, means that the same melody, and the same chord, may be played in any key simply by moving the starting position of one's hands on the keyboard; the relative positions of the keys that can be used to play the melody or the chord do not change.
While it would be possible, by having the three keys in a column play notes of pitch differing by a syntonic comma, to adapt a Jankó keyboard to the 53-note scale, the result would, in order to be uniform, disperse the notes belonging to a particular conventional scale in just intonation over at least four rows of the keyboard.
The keyboard of the Enharmonic Harmonium of Bosanquet, an instrument for playing music in the 53-note scale,

did indeed have a resemblance to the Jankó keyboard, and therefore was doubtless designed so that a uniform displacement on the keyboard would be equivalent to a uniform number of steps in the 53-note scale.
Here is another alternate keyboard design:
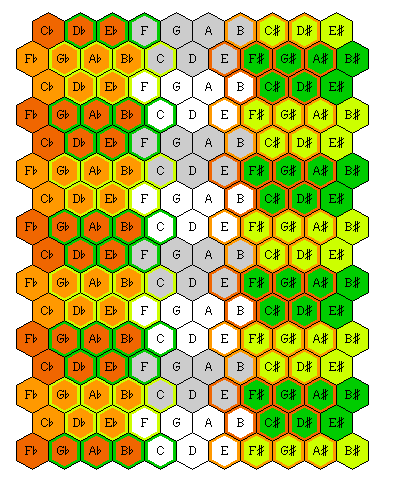
This is the Wicki-Hayden keyboard. Here, the hexagons that are directly above one another represent notes an octave higher. A melody in any key involves a sequence of notes in the same relative positions on the keyboard, since each displacement represents the same number of semitones. It is suited to meantone temperaments as well as equal temperament.
In the diagram above, one objection to the Wicki-Hayden keyboard is dealt with. Since notes separated by one semitone are not adjacent, or in a simple relation to each other, the keyboard has been widened slightly, and the columns of flats, naturals, and sharps each have a light and a dark color used for them, so that it is obvious where the note that corresponds to a given note among the flats or among the sharps is located. Also, as moving one whole tone above a flat yields a sharp, and one whole tone below a sharp yields a flat, some hexagons have borders indicating alternate locations for the accidentals due to enharmonic spellings.
|
So far, we have seen exotic keyboards that have seen little actual use in practice. However, in a number of European countries, accordions, instead of having a conventional piano keyboard on one side, and chord buttons arranged in columns according to the circle of fifths on the other side, use an unconventional keyboard arrangement which allows the accordion to cover a greater range of octaves.

Illustrated above are the two common alternating forms of what is called the chromatic button keyboard for the accordion. Three rows represent all the notes, but to simplify fingering, the top two rows are duplicates of the bottom two rows. The gently sloping green lines identify which buttons correspond to which keys on a conventional piano keyboard, passing through the centers of those buttons which correspond to a given note.
Thus, it is possible to begin a group of buttons, three wide and four high, with any of the twelve notes of the octave in the lower left corner, for example, which means that merely by changing the starting position of the hands, a melody can be played with the same fingering in any key on this style of keyboard as well.
On some accordions, the buttons on the other side form a mirror image of this arrangement, rather than following the Stradella arrangement of chord buttons; such an accordion is called a free-bass accordion.
One idea that had occurred to me is that one could imagine an alien music in which the harmonic ratio of 1:3 played a primary role, and that of 1:2 played a secondary role. Thus, the gamut would be composed of repeated twelfths instead of octaves. I see, however, that someone else has had the same idea, but in a more radical form, dispensing with the 1:2 ratio entirely, and basing the frequencies of notes in just intonation on the ratios 1:3, 1:5, and 1:7; the result is the Bohlen-Pierce scale. Note, however, that what I was thinking of would have been very different in practice from the Bohlen-Pierce scale; music performed in that scale sounds strikingly different from conventional music, whereas in the type of scale I was thinking of, it would be difficult to notice much difference without looking at the score.