
Many books on music include a diagram somewhat like the one below:

However, those diagrams are not usually exactly like this one. For one thing, they usually start with the note C, while this diagram starts with the note F. Also, the notes all have the same time value, and there are no rests.
The diagram depicts a musical note, and the first few of its harmonic overtones. To bring out how the same notes repeat from one octave to the next, the sequence of notes occupying an octave is made to fit in a bar, by adjusting the time value of notes from octave to octave. Also, since the Western musical scale is based on harmonics at 2x, 3x, and 5x a given frequency, ignoring any harmonic which includes a higher prime number, those notes which do not relate to the Western musical scale, instead of being depicted imperfectly, are shown as having no representation through the use of rests. (Incidentally, the book On the Sensations of Tone by Hermann Helmholtz did feature a diagram of the harmonic series having this general character, rather than the form most commonly used.)
To show the development of all seven of the notes in the diatonic scale, however, it is necessary to start the diagram at a lower pitch:
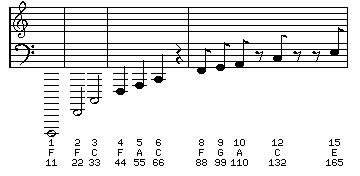
and continue it for a greater length.

Here, the overtones of an 11 Hz note are shown. Actually, 11Hz is an inaudible infrasonic frequency, although 16 Hz (16.5 Hz in the scale shown here) is a very low C sometimes found in some organ music. This illustrates why the pitch which sets the A above middle C to 440 Hz was chosen as the current standard; in addition to corresponding roughly to the concert pitch of the day when the standard was established (there is a tendency for one musician or musical group to play slightly higher in pitch than the next one, as it makes his music seem to sound "better"; this has reduced the utility of Stradivarius violins because they were constructed to function under a lower pitch standard), Hermann Helmholtz had used 440 Hz because the other notes of the octave, in just intonation, would also have frequencies which were an integral number of cycles per second.
It is because natural sounds are often accompanied by frequencies that are integer multiples of the lowest frequency present, and because our ears also add such frequencies as distortion, that sounds with frequencies in simple integer ratios are felt to be in harmony with each other. In terms of the lengths of strings, instead of actual sound vibrations, which were not yet accessible to study, this was realized by Pythagoras.
How the Western musical scale is constructed, based on the following principles:
can be illustrated by a two-dimensional diagram:
F 27/20 A 27/16 C# 135/128 E# 675/512 Bb 9/5 D 9/8 F# 45/32 A# 225/128 Eb 6/5 G 3/2 B 15/8 D# 75/64 Ab 8/5 C 1 E 5/4 G# 25/16 Db 16/15 F 4/3 A 5/3 C# 25/24 Gb 64/45 Bb 16/9 D 10/9 F# 25/18 Cb 256/135 Eb 32/27 G 40/27 B 50/27
Each note is followed by the ratio of its pitch to that of C. Moving one step up multiplies the frequency of a note by 3/2, moving one step to the right multiplies the frequency of a note by 5/4, except that 2 is multiplied or divided as needed to keep the note in its proper position on the scale.
The seven notes of the diatonic scale are shown in bold on the diagram. In most Western music, melodies are composed of sections in which seven notes are used, corresponding to the seven notes with letter names, or the white keys on the piano. But although the notes correspond to these seven notes, it is not always true that they are those seven notes.
Sections of a musical piece may be in one key or another. If part of a song is in the key of C, then that means the seven notes with letter names are the notes that are used. If it is in the key of G, however, then G corresponds to C (it is the tonic of the scale) and the other six notes of the diatonic scale are also shifted by an equal amount.
As most people know, without being particularly familiar with music, the note produced by the black key on the piano that is between the white keys for the notes A and B can be called either A sharp, because it is higher in pitch than A, but not as high as B, or B flat, because it is lower in pitch than B, but not as low as A.
But it is because these notes can be used to play a piece of music in which the seven-note diatonic scale is displaced that at some times calling it A sharp, and at other times, calling it B flat, is considered appropriate. This is called musical "spelling". Thus, a B flat belongs to the keys of F, B flat, E flat, A flat, D flat, and G flat, and an A sharp belongs to the keys of F sharp and B.
One reason for this convention has to do with how key signatures are written on the musical staff. If I take the seven bold notes in the diagram above, and overlay them so that the C is on top of the F in another copy of the whole diagram, then I am making F correspond to C, to illustrate the key of F. The note corresponding to F is B flat. It is more convenient to call it B flat than to call it A sharp, because the note corresponding to E is A, so A is already used, but there is no note that has B corresponding to it. Therefore, in the key signature for the key of F, a flat is placed on the row for the note B, because B flat is used in that key and B is not, while the row for the note A is left without an annotation, because the note A is used.
The degrees of the scale, which are the notes considered relative to the tonic of the musical piece being played, or within the key of that piece, as opposed to the notes referred to by their absolute frequencies, are named as follows:
Corresponds to notes: Mode starting here:
Do Tonic C G D A E B C F Bb Eb Ab Db Major (Ionian)
Re Supertonic D A E B F# C# D G C F Bb Eb Dorian
Mi Mediant E B F# C# G# D# E A D G C F Phrygian
Fa Subdominant F C G D A E F Bb Eb Ab Db Gb Lydian
So Dominant G D A E B F# G C F Bb Eb Ab Mixolydian
La Submediant A E B F# C# G# A D G C F Bb Minor (Aeolian)
Ti Subtonic B F# C# G# D# A# B E A D G C Locrian
thus, "the note that corresponds to C" is the Tonic, "the note that corresponds to D" is the Supertonic, and so on.
The column with E at the top illustrates the notes in the scale of E major. The set of notes used for the key of C major is also the set of notes used for the key of A minor. Major and minor are examples of modes, and the final column gives the name of the mode with that degree of the diatonic scale as its tonic.
Note that while the mode beginning with C is the most natural musical mode, the less harmonious minor mode was regarded as more serious, and hence more suitable for church music. Since it was in that context that much of Western musical notation developed, that is why the minor mode, rather than the major mode, starts with A when played on the white keys of the piano.
For the different keys of the major mode, another way to see why the tonic moves by a fifth when a sharp or flat is added or subtracted to the key signature, is this chart, showing the twelve notes of the equal-tempered scale with equal spacing:
Note: C Db D Eb E F Gb G Ab A Bb B
-------------------------------------
Gb So La Ti Do Re Mi Fa
Db Ti Do Re Mi Fa So La
Ab Mi Fa So La Ti Do Re
Eb La Ti Do Re Mi Fa So
Bb Re Mi Fa So La Ti Do
F So La Ti Do Re Mi Fa
C Do Re Mi Fa So La Ti
G Fa So La Ti Do Re Mi
D Ti Do Re Mi Fa So La
A Mi Fa So La Ti Do Re
E La Ti Do Re Mi Fa So
B Re Mi Fa So La Ti Do
F# So La Ti Do Re Mi Fa
-------------------------------------
C C# D D# E F F# G G# A A# B
Note that when the frequency of a note is multiplied or divided by the ratio of 81/80, a note is obtained with the same name. Therefore, this interval is called the syntonic comma.
The equal-tempered scale to which most instruments are tuned is an attempt to approximate the frequencies of the notes derived from the integer harmonics. Other approximations are possible, but less convenient; in addition to using 5 or 7 equally spaced notes, as an alternative to a scale of 12 equally spaced notes, one could use 19 equally spaced notes (the 2:3 ratio is less well approximated, but the 4:5 ratio is better approximated) or 53 equally spaced notes (which is very close to an exact fit), or even 9 equally spaced notes, similar to the Pélog tuning used for gamelan music, just as 5 equally spaced notes resembles the Salendro tuning.
Note Just 5 7 9 12 19 53 C 264 252.71 268.18 277.18 (1) 261.63 (1) 264.02 (1) 264.20 (1) D 297 290.29 296.10 299.37 (2) 293.66 (3) 294.56 (4) 297.21 (10) E 330 326.92 323.34 (3) 329.63 (5) 326.62 (7) 329.99 (18) F 352 333.46 360.95 377.19 (5) 349.23 (6) 353.50 (9) 352.29 (23) G 396 383.04 398.52 407.38 (6) 392.00 (8) 394.39 (12) 396.29 (32) A 440 440 440 440 (7) 440 (10) 440 (15) 440 (40) B 495 485.80 475.23 (8) 493.88 (12) 490.89 (18) 494.96 (49)
In the case of the temperaments with 9, 12, 19 or 53 notes to the scale, the number in parentheses shows which note in the scale is being used.
The intervals, or ratios between the frequencies of two notes, in the Western musical scale are called by these names:
Name: Frequency Distance in Distance on Distance in
ratio: semitones: the 53-unit scale: cents:
Unison 1:1 0 0 0
Minor second 16:15 1 5 111.7
Major second 9:8 or 10:9 2 9 or 8 203.9 or 182.4
Minor third 6:5 3 14 315.6
Major third 5:4 4 17 386.3
Perfect fourth 4:3 5 22 498.0
Augmented fourth 45:32 or 25:18 6 26 or 25 590.2 or 568.7
Diminished fifth 64:45 or 36:25 6 27 or 28 609.8 or 631.3
Perfect fifth 3:2 7 31 702.0
Minor sixth 8:5 8 36 813.7
Major sixth 5:3 9 39 884.4
Minor seventh 16:9 or 9:5 10 44 or 45 996.1 or 1017.6
Major seventh 15:8 11 48 1088.3
Octave 2:1 12 53 1200
and these intervals are the basic elements of the chords used in music. Those for the tritone, that is, for the two intervals corresponding to a distance of 6 semitones, the augmented fourth and the diminished fifth, are not to be taken too seriously, however.
Thus, a major chord consists of three notes in 4:5:6 ratio, a major third followed by a minor third, and a minor chord conists of three notes in 10:12:15 ratio, a minor third followed by a major third.
Just as a tritone, an interval of six semitones, in the equal tempered scale is merely a discord, not corresponding to the ratios given here for either the augmented fourth or the diminished fifth, a diminished seventh chord consists of four notes, each note three semitones away from the preceding one, is a chord that should be thought about in equal-tempered terms rather than as an approximation to any set of integer ratios, on the other hand.
The two-dimensional chart shown above can be sloped over slightly:

and in this way, notes having the same spelling can be directly above one another.
Thus, the notes called "C" form a vertical line, which include the starting point, with the value 1, and also other values at regular intervals, such as 6561/6400, 81/80 and 80/81. Since the ratio between two adjacent dots in that line is constant at 81/80, one could think of placing any note called C, based on its frequency, somewhere on that line.
The notes of the equal-tempered tuning, starting with C=1, are illustrated on the diagram by a line of dots enclosed in diamonds.
There is also a line of dots enclosed in squares, and another line of circled dots in the diagram. They represent quarter-comma meantone tuning and Silbermann's one-sixth-comma meantone tuning.Quarter-comma meantone tuning was used to tune some older organs. Essentially, the notes on the organ are tuned on the basis of a perfect fifth that has been flattened by the fourth root of the syntonic comma, so that while the fifths are not accurate, the major thirds are exact. Since flat notes and sharp notes are different in this tuning, as can be seen from the fact that the line representing it has a slope different from that for the equal-tempered tuning, discords arise in music that uses keys which are transposed too many fifths away from the key of C: since a keyboard only has five black keys in addition to the seven keys of the diatonic scale, only five additional keys will have all seven notes forming a diatonic scale having the same pitch relationships as that of the scale provided for the key of C.
Another straight line passing through C=1 on the diagram is the line that was vertical in the original diagram, but is now tilted: the notes formed by an exact perfect fifth of 3/2. This tuning is called the Pythagorean tuning, and the ratio between B sharp (not shown on the diagram) and C on that tuning is called the Pythagorean comma, as distinct from the syntonic comma.
The syntonic comma is so named because it is the distance between two notes with the same spelling, thus representing the same tone.
Except for equal temperament, the simple temperaments shown in the diagram, the Pythagorean temperament, the 1/4-comma meantone temperament, and the 1/6-comma meantone temperament, produce a uniform result for a limited range of keys. Thus, for purely diatonic music, using only the seven basic notes of the octave, if one has twelve notes of the circle of fifths tuned so that eleven of the steps between them are the same, but one left-over step is radically different, then you can use notes 1 to 7, 2 to 8, 3 to 9, 4 to 10, and 5 to 11. In other words, music can be played in five different keys with such a simple temperament.
This diagram illustrates the version of the circle of fifths applicable to the 53-note equally-tempered scale:
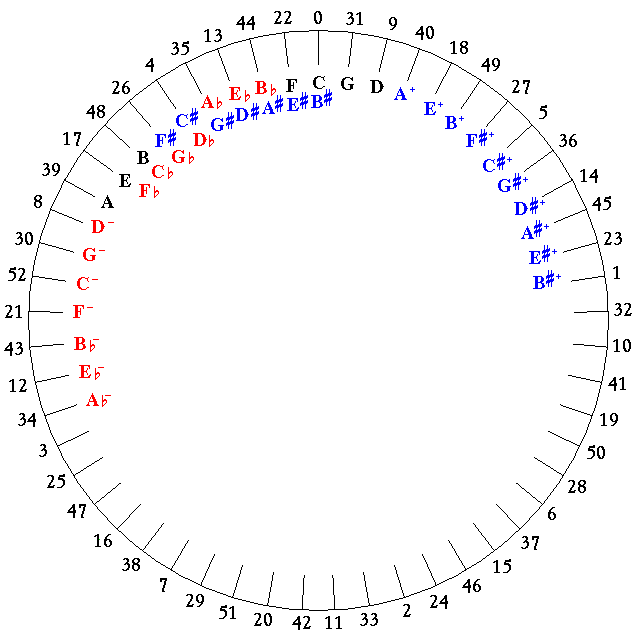
Note how those notes with different spelling the ideal just pitches of which differ from each other only by amounts on the order of a schisma are assigned to the same step on the 53-note scale.
Also, note that the usual progression between keys by a fifth leads to notes with the same spelling which differ by a syntonic comma, noted by - or + after the name of the note. On the far end of the chart, where the names of the notes are not filled in, the difference in syntonic commas finally adds up to a semitone.
This table shows how the 53-note scale, with the note spellings shown, ties in with the two-dimensional chart of just intonation:
37 Ab++ 6561/4000 1 C+ 81/80 18 E+ 81/64 35 G# 405/256 52 B#- 2025/2048
6 Db++ 2187/2000 23 F+ 27/20 40 A+ 27/16 4 C# 135/128 21 E#- 675/512
28 Gb++ 729/500 45 Bb+ 9/5 9 D 9/8 26 F# 45/32 43 A#- 225/128
50 Cb++ 243/250 14 Eb+ 6/5 31 G 3/2 48 B 15/8 12 D#- 75/64
19 Fb++ 32/25 36 Ab+ 8/5 0 C 1 17 E 5/4 34 G#- 25/16 41 B#-- 125/64
5 Db+ 16/15 22 F 4/3 39 A 5/3 3 C#- 25/24 10 E#-- 125/96
27 Gb+ 64/45 44 Bb 16/9 8 D- 10/9 25 F#- 25/18 32 A#-- 125/72
49 Cb+ 256/135 13 Eb 32/27 30 G- 40/27 47 B- 50/27 1 D#-- 125/108
Major thirds move quickly around the 53-note circle of fifths, because of the decimation chosen to give preference to the fifth as representing the smallest change.
Some people have criticized the equal-tempered scale, on the basis that in that scale, while the perfect fifth is a close approximation to the actual 3:2 ratio, the major third is not a very good approximation to the actual 5:4 ratio; and, furthermore, that the major third is more important to the harmonic structure of music.
While the quarter-comma meantone temperament favors the major third, it is a straight-line temperament, and thus it does not permit modulations around the circle of fifths, or even going very far in one direction without a large number of different versions of each note.
However, if the octave were divided equally into 25 notes, with the distance between two of them replacing a semitone, then the 5:4 ratio of 386.3 cents would be approximated by 384 cents instead of by 400 cents, a much closer approximation.
The perfect fifth of 702.0 cents, approximated by 700 cents in the equal-tempered scale, could be approximated by a displacement of 15 notes, at 720 cents, as 14 notes, or 7 shrunken semitones, would be less accurate, at 672 cents.
The resulting scale would look like this:
* * * * * * * * * * * * * * * * * *
0 5 8 10 15 18 23 25
C D E F G A B C
with the asterisks representing the "black keys" required for a keyboard for this equal-tempered quarter-tone scale which would allow unlimited modulation while retaining an accurate major third - at the cost of an inaccurate perfect fifth.
The result of this is that, instead of having a circle of twelve perfect fifths which runs through four different circles of three major thirds, the musical landscape consists of a circle of twenty-five major thirds which runs through five different circles of five perfect fifths.
If one accepts that the fifth of the equal-tempered scale is fully acceptable, and furthermore, one desires to be able to play existing music which assumes a closed circle of fifths of twelve degrees, but finds the sharpening of the major third in the equal-tempered scale unacceptable, another alternative would simply be, when in the key of C, to flatten E, A, and B by 6.85 cents, and sharpen C, F, and G by 6.85 sets, while leaving D alone, as it could be part of either the D-F-A minor triad or the G-B-D major triad. and similary, for whatever key the music being played is in, sharpen do, fa, and so by 6.85 cents and flatten mi, la, and ti by 6.85 cents. This approximation would, under the assumption that only the major third is the problem, obtain most of the benefits of just intonation in a very simple fashion.
Another option is to divide the scale into 31 equal divisions of about 38.71 cents each. A major third of about 386.3 cents is closely approximated by ten of these divisions at 387.1 cents. The perfect fifth of about 702 cents is less closely approximated by 18 of these divisions at 696.8 cents.
In 1555, Nicola Vicentino described an instrument with a keyboard that provided 31 notes to the octave based on this scale.
It was laid out like this, in two manuals:
| | | | | | | | | | | | | | | 5 | |10 | | |18 | |23 | |28 | | | |___| |___| | |___| |___| |___| | | | | | | | | | | | | | | | | 4 | | 9 | | |17 | |22 | |27 | | | |___| |___| | |___| |___| |___| | | | | | | | | | | 1 | 6 | 11 | 14 | 19 | 24 | 29 | |_______|_______|_______|_______|_______|_______|_______| | | | | | | | | | | | | | | | | |30 | | 3 | | 7 | |12 | |16 | |21 | |25 | |30 | |___| |___| |___| |___| |___| |___| |___| |___| | | | | | | | | | | | | | | | 2 | | 8 | | |15 | |20 | |26 | | | |___| |___| | |___| |___| |___| | | | | | | | | | | 0 | 5 | 10 | 13 | 18 | 23 | 28 | |_______|_______|_______|_______|_______|_______|_______|
The tuning of this keyboard, according to a diagram showing the pitch of each key in cents which I used as my source to derive the sequence of notes, is more complicated than shown here, as some keys differing by 1 in the sequence differ by about 41 cents instead of about 39 cents. The numbers duplicated in the top row of the upper manual actually represent slightly higher pitches than the keys with the same number on the lower manual because of this.
Apparently, though, this is because the diagram followed the analysis of the description of the Archicembalo's tuning given by Karol Berger; the main text of the Wikipedia article, although it mentions Karol Berger's analysis as an alternative, is written on the basis of a strict tuning according to the 31-note division of the octave; so this is apparently still a point in question.
So even the basic tuning does what the alternate tuning, to be described below, aimes at: to allow fifths to be played that approximate just intonation more closely than a pure equal division of the octave into 31 parts would allow.
An alternate tuning for this keyboard was also described, in which the notes of the upper manual, instead of being one step higher in the equal division of the octave into 31 parts, would be tuned a quarter of a comma higher than those of the lower manual. This meant that pieces could not be played in a fully chromatic manner, going fully around the circle of major thirds, but better perfect fifths could now be played, permitting pieces to be played in a close approximation to just intonation.
A footnote in Sir John Hawkins' A General History of the Science and Practice of Music states:
The practice has long been, in tuning the organ and such like instruments, to make the fifths as flat, and the thirds as sharp, as the ear will bear, which necessarily induces an inequality in the tones.
The quarter-comma meantone temperament makes the thirds exact, while equal temperament favors the fifths. If both were given equal weight, a one-fifth comma meantone temperament would be a possible result: a fifth would be one-fifth of a comma below a perfect fifth, and since a third is formed by four fifths in a row, which is why depressing the perfect fifth by a quarter of a syntonic comma causes four of them to yield an exact major third, since one-fifth of a comma is one-twentieth of a comma short of one-quarter comma, the error in the third would also be one-fifth of a comma. As noted, though, the thirds are said to be more important in practice, and so this could refer to something else, such as Silbermann's one-sixth comma temperament; one can't really conclude that a one-fifth comma meantone tuning was used in Hawkins' day.
Traditional Chinese music was based on the Pythagorean scale, starting from a note having a frequency of about 600 Hz, called "Yellow Bell". One source notes old instruments having pitches of 591 and 597 Hz for that note, and another gives the pitch of that note as being 601.5 Hz.
However, it should also be mentioned that the equal-tempered scale was first worked out and described by Chu Tsai-Yu during the Ming Dynasty, who published this work in 1584, before the Western formulation of the equal-tempered scale by Andreas Werckmeister in 1691.
Some works on Chinese music treat "Yellow Bell" as corresponding to C. With that correspondence, however, the Chinese diatonic scale does not include B, but it does include F# (and not F). So that note really corresponds to the note F in function, although its pitch is close to that of D in Western music.
Thus, the basic Chinese diatonic scale, in the sense that C major is the basic diatonic scale of Western music, is approximated by the key of A major.
I remember seeing a chart in a classroom that said that the note C had the frequency of 256 cycles per second. This was before that came to be called 256 Hertz.
It turns out this was according to a standard called Scientific Pitch, devised in 1713 by Joseph Sauveur. With equal-tempered tuning, A would be 430.54 Hz in this scale - not 432 Hz, as apparently some mistakenly suppose.
It is a genuine historical fact that pitch inflation took place as a form of one-upmanship among orchestras; thus, Wikipedia notes that tuning forks in the Paris Opera were based on A=423 in 1810, A=432 in 1822, and A=449 in 1855. Being asked to sing at a higher pitch is a problem for singers, and so a number of them had complained about this even before Giuseppe Verdi became noted as championing their cause.
A French law of February 16, 1859 established a concert pith of A=435 in order to halt and reverse this problematic trend.
The modern standard pitch of A=440 was recommended in 1834 by a conference in Stuttgart, deriving from work done by Johann Scheibler with an instrument he called the Tonometer, with which he determined the numerical values of the frequencies of musical tones by counting the beats produced from sounding two suitable tuning forks at once.
This work was cited by Hermann Helmholtz in On the Sensations of Tone, where I first encounted the fact that, because 440 is a multiple of 40, making A=440 allows the other notes in the octave, when in just intonation rather than equal temperament, to also have integer frequencies.
A geophysical phenomenon called the Schumann Resonance, which averages to 7.83 Hz, has been used as an argument for using 8 Hz as a basis for music, thereby going to the A=432 pitch. Actually, 8 Hz would go to 430.54 Hz, as noted above, and if 7.83 Hz is used as a basis, the result would be even lower. 7.83 Hertz, times 32, gives 250.56 Hz for C, and therefore 421.39 Hz for A.
Of course, that rationale is the veriest pseudoscience.
Furthermore, it hardly helps that one notable advocate of a concert pitch of A=432 Hz was the infamous Lyndon LaRouche.
But since pitch inflation is real, and the current concert pitch does not sit well with the limits of the human voice and the operatic repertoire, or with the design of Stradivarius violins, which, to play at modern concert pitch, need to have their strings at levels of tension for which they were not designed, there is a strong argument for reforming concert pitch to a value consistent with the classical period.
We can't just play everything in a key that is one semitone lower, as that would be equivalent to a concert pitch of A=415.3 Hz, which I had thought to be lower than any possible value of the old concert pitch.
Alexander John Ellis, who was an acquaintance of Alexander Graham Bell, and who translated On the Sensations of Tone into English, also used a Tonometer to continue and extend the work of Johann Scheiber, in measuring the frequencies of a significant number of tuning forks from various periods.
In his paper, The History of Musical Pitch, published in the March 5, 1880 issue of the Journal for the Society of Arts, and continued in the April 2, 1880 issue of that journal, he came to the conclusion that tuning forks with pitches from A=415 to A=428 represented the "Common pitch for two centuries", with pitches above and below that being placed in other categories.
From his table, after some thought, I've decided that A=423 Hz, rather than 432 Hz, ought to be recommended as the standard best representing the classical period; a tuning fork belonging to Mozart was at 422 Hz, one belonging to Handel was at 423 Hz, and the original pitch standard of the Philharmonic Society of London, from 1813, which was also the year in which it was founded, was 424 Hz, which pitch was also recommended by a distinguished musician in 1619. So it might appear that this is where the best examples are clustered around.