
In addition to the four traditional instruments of the violin family, and various intermediate instruments proposed from time to time, such as Carleen Hutchins' Violin Octet, mentioned above, violin family instruments in a number of other sizes exist.
These, however, although they differ in size, have their strings tuned to the same pitches as the regular instruments to which they correspond.
Thus, you may see advertisements for violins which, instead of having the standard size, called 4/4 size, are in sizes ranging from 7/8 down to 1/32. The fractions are conventional names for the sizes; a 1/2 violin is not actually one-half the length of a regular violin. These are intended to allow young children to have instruments suited to them as they learn to play the violin.
A Sears, Roebuck catalog from 1912 notes that one of the violins offered is also available in 3/4 size, "especially adapted for children from 9 to 14 years of age", and another is also available in "ladies' or 7/8 size"; the 1/2 size and 3/4 size for violins are also referenced in a 1917 catalog of John Friedrich and Brother, so this fractional notation for violin sizes predates the introduction of the Suzuki method of violin teaching in the postwar era.
A French book, "L'Art du Luthier", from 1903, gives an extensive table of recommended dimensions for different instruments of the violin family, in millimetres, from which I will give the value for the length of the body:
Violin, 1/4 size 297 mm Violin, 1/2 size 302 mm Violin, 3/4 size 332 mm Violin 358 mm Viola (large model) 473 mm Cello, 3/4 size 653 mm Cello 770 mm Double Bass 1m 130 mm
An even older source, from 1895, gives 14 1/8" as the body height of a full-size violin, 13 7/8" as that of a ladies' violin (not explicitly referred to as 7/8 size), and 13 1/8" as that of a three-quarter size violin, and I have now seen references in English to the three-quarter violin as early as 1866.
A German book, from 1892, gives these dimensions for a number of instruments from the violin family:
Violin, 1/2 size 320 mm Violin, 3/4 size 335 mm Violin 360 mm Viola 400 mm Cello 760 mm Double Bass, 1/2 size 1m 105 mm Double Bass, 3/4 size 1m 108 mm Double Bass 1m 110 mm
Here, the viola is definitely one based on a small-size model, Stradivarius' small model being 411 mm long.
Another source gives the body size for a 7/8 violin as 343 mm, but it gives that for a full-size violin as 355 mm (14") rather than 358 mm (14 1/8").
A web site giving modern values for different fractional sizes of the violin, however, gives considerably different values for the sizes, and so does a second modern web site, and then I found slightly different values in a PDF document on yet a third site, and significantly different ones on a fourth site in French, and I give the sizes from all four below:
Violin 356 mm 355 mm 356 mm 355 mm Violin, 7/8 size 345 mm 345 mm Violin, 3/4 size 335 mm 335 mm 335 mm 330 mm Violin, 1/2 size 310 mm 320 mm 320 mm 317 mm Violin, 1/4 size 280 mm 285 mm 285 mm 292 mm Violin, 1/8 size 255 mm 255 mm 260 mm Violin, 1/10 size 235 mm Violin, 1/16 size 230 mm 230 mm 216 mm Violin, 1/32 size 215 mm
and the first of these sites also notes that Suzuki sizes for 1/10 and 1/16 violins are significantly smaller than the traditional sizes, being similar to 1/16 and 1/32 sizes on that scale respectively; the sizes given on the fourth of those sites seem to correspond to that.
The dimensions from the third source at least seem to reflect the best dimensions available from the first two, but I'm not decided as to whether I should regard it as authoritative, or possibly derived from an inconsistent mixture of sizes from other sources. Perhaps plotting these sizes, and the old French ones, on a graph might help me see if there is some system to this.
Of course, neither 302 mm nor 310 mm nor 320 mm is anywhere near half of 358 mm; if we were to divide 358 mm by the cube root of 2, the result is 284 mm, so the fractions do not even represent volume.
Since 1/4 size is 285 mm in some cases, I suppose one could try the sixth root of each fraction. That would give:
4/4, full size 356 mm 7/8 348 mm 346 mm 3/4 339 mm 336 mm 1/2 317 mm 3/8 302 mm 299 mm 1/4 283 mm 3/16 269 mm 267 mm 1/8 252 mm 1/10 242 mm 238 mm 1/16 224 mm 1/20 216 mm 212 mm 1/32 200 mm
These sizes don't correspond too badly to the modern values given in the previous table, except that the "1/32" violin would have to be called a "1/20" violin instead, which perhaps splits the difference between "traditional" and "Suzuki" sizes.
On further reflection, it seems likely to me that the fractions should be considered to be merely conventional sizes, for steps in a uniform logarithmic scale of sizes, with the additional 7/8 fraction indicating an intermediate step. So either 3/16 or 1/5 would indicate the same size, halfway between the 1/4 and 1/8 sizes. Sizes on that basis are shown in the second column; only those for the intermediate values are changed, generally becoming slightly smaller.
The values for 1/2 size and 1/4 size in the French source seem to be so close to each other (and to the size given as that of a 3/8 violin above) that it doesn't seem that those sizes could be the basis for a systematic scale.
In proportion to the ideal size for a viola, the actual size of the instruments commonly in use is equivalent to that of a violin 275 mm in length. Thus, a viola is really a "1/4 size" viola, or thereabouts, which makes it quite understandable that its sound quality is compromised. While the cello and double bass are also available in smaller sizes described in fractional terms, smaller size violas instead have their sizes given directly in inches of body size.
Incidentally, the usual size for a double bass is considered not to be the full size for a double bass, but instead its 3/4 size. Full size is considered to be 1 metre, 160 mm, and 3/4 size 1 metre, 110 mm, so the size for the double bass given in the old French book quoted above is intermediate between these two values. On the other hand, the old German book quoted above gives exactly the current 3/4 size usually used as the full size for a double bass.
The 1912 Sears, Roebuck catalog noted above advertises both 3/4 and 1/2 double basses, but no full size ones, so this would seem to corroborate that the usual size is designated the 3/4 size.
Also, Antonio Stradivarius made at least a few small violins. Two of them, the 'Cipriani Potter' from 1683, and the 'Belle Skinner' from 1736, have a body height of 339 mm, which would seem to make them 3/4 size violins (although I have seen the Cipriani Potter referred to as a 7/8), and another, the 'King Maximillian Joseph' from 1702, has a body height of 347 mm, which would seem to make it a 7/8 violin. The 'Gillott' from 1720, having a 267 mm body size, doesn't correspond to one of the more usual values, yet it is close to being midway between the size of a 1/4 violin and a 1/8 violin, which suggests that a standardized system of sizes for violins has long been in existence.
A paper discussing violin sizes which I encountered showed examples made by three different members of the Amati family, along with another example by Lorenzo Storioni. Another source notes that Andrea Amati, in addition to 355 mm full-sized violins, also made some of 342 mm, or 7/8 size.
I was surprised that the sizes Antonio Stradivari used for small violins were, almost to the millimetre, the same as those I had listed in my final attempt at laying out standardized values for the fractional sizes of violins.
Of course, the fact that the ratio between the sizes of a full-sized violin and a 1/2 size violin was the sixth root of two, and thus if one adds in the 3/4 size violin in a uniform logarithmic scale, the ratio between successive sizes is the twelfth root of two - which is, of course, a value very familiar from earlier pages in this section, as it is the ratio between frequencies, and also wavelengths, and therefore string lengths, for successive notes one semitone apart in the equal-tempered scale.
But at first this seemed to be an amusing coincidence, or due to perhaps some sentimental attachment on the part of violin makers. But perhaps it might simplify memorizing the appropriate placement of one's fingers when playing a violin and moving across different sizes of instruments.
Stradivarius also made a few guitars. And what would be more reasonable than that if there is a need for reduced-size violins for younger players, the same might apply to guitars? And why not use the same set of sizes for both instruments?

And then the obvious dawned on me. If the ratio between instrument sizes is the same as the ratio between string lengths for successive notes, then a single template or jig would suffice either directly, or for the making of jigs for the individual instruments, to control the placement of frets on the fretboard of a fretted instrument such as a guitar.
Of course, on a violin, it isn't the size of the body that determines the spacing between fingers on the fingerboard, it is the distance between the nut and the bridge. And an analogous rule applies to the guitar. In the case of the violin, one can see from the image above comparing the violin and the cello that not only is the cello proportionately thicker, but its neck is proportionately shorter. And some small-sized violins have necks that are larger in proportion than on a regular violin, to make fingering more convenient: the instrument may be intended as an easily portable one for an adult player instead of one suited to a child.
However, it may be that the fractional sizes I have worked out, while they were at one time the traditional sizes for smaller violins, are not the sizes used most often at present. After all, violins don't have frets, so the issue I've identified that would encourage the particular sizes I've proposed for guitars doesn't really exist for the violin.
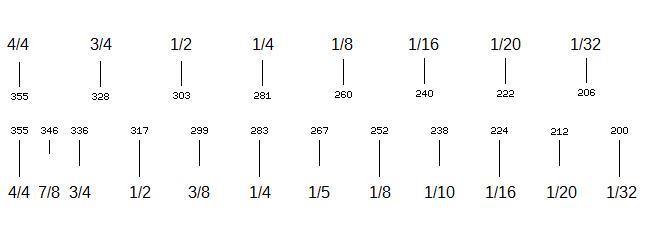
I have seen the figure of 92.5% as the ratio between successive sizes quoted in a few places. However, another source gives 92% instead, specifically saying each size is 8% smaller than the previous one.
And if the fractions are merely conventional sizes, could it be that the steps between 4/4, 3/4, and 1/2 are the same as those between 1/2, 1/4, and 1/8?
Given that the sizes normally seen today are 4/4, 3/4, 1/2, 1/4, 1/8, 1/16, 1/20, and 1/32 - and also providing a nice explanation for the fact that when 1/20 was inserted for instruments used under the Suzuki system, it had the same size as 1/32 as used by others... could it be that 3/4 is no longer being treated as at a half step, and instead the size of a full step has been shrunk, so that things average out, making the sizes of at least some of the violins in the sequence still similar?
The image above compares violin body sizes, along a logarithmic scale, between, on the lower scale, the traditional system I have inferred, and on the upper scale, the possible modern system that I am now suspecting may exist as an alternative.
Thus, to sum up, I think that the fractional sizes should be as follows:
Violin Cello Bass
4/4, full size 355 mm (14") 759 mm (29 7/8")
7/8 346 mm 737 mm
3/4 336 mm 716 mm 1m 110 mm (43 11/16")
1/2 317 mm 676 mm 1m 48 mm
3/8 299 mm 638 mm 989 mm
1/4 283 mm 602 mm 934 mm
3/16 267 mm 569 mm 881 mm
1/8 252 mm 537 mm 832 mm
1/10 238 mm 507 mm 785 mm
1/16 224 mm 478 mm 741 mm
1/20 212 mm 451 mm 699 mm
1/32 200 mm 426 mm 660 mm
In the case of the viola, however, the instrument is considered to be so much smaller than its just proportion, even in its largest normal size of 17 inches body size, that the string instrument trade has just given up assigning fractional sizes to them.
Instead, in the English-speaking world, violas are sold with body size quoted in inches. Thus, one company that makes string instruments sells violas in the following sizes: 17", 16 1/2", 16", 15 1/2", 15", 14", 13", 12", and 11", with the specific sizes available varying by model; the student model is not available in 17", and a more advanced model of higher quality is not available in 11".
A 14" viola is hard to tell at sight from a 4/4 violin; however, in addition to being strung differently, it should have a larger rib height, and, as well, the design of its bridge should differ.
For a violin with a 355 mm body, the scale length - the length of the strings from the nut to the bridge - is usually 328 mm. The scale length, combined with the pitch of the note to be played on the open string, determines what type of string is to be used for the instrument.
As a 1/10 size violin is seven stops smaller than a 4/4 violin, the D, A, and E strings of such a violin would be made from the same material as the G, D, and A strings of a full-size violin, since, being 2/3 the length, they would sound a fifth higher under the same tension.
In the case of a 14" viola, as that is the same size as a 4/4 violin, one would expect that the strings they share, the G, D, and A strings, would be the same on both. If one applied such a simplistic analysis to the cello, though, one would certainly be wrong, as the neck of a cello is shorter, in proportion to its body, than that of a violin. This is true to some extent of the viola as well, so the vibrating string length of a 14" viola may be 319 mm, not 328 mm. This would mean that its G, D, and A strings should actually be made from the same material as the corresponding strings of a 7/8 violin.
However, one may have to do with strings made for either a 4/4 violin or a 3/4 violin. As a considerable variation in string tension is possible, it is not needed to offer an immense variety of strings differing in very small steps of thickness. Thus, for example, one major company offering strings for many different types of stringed instruments offers three thickness classes of string for violins for a few of their string brands (they have a wide choice of different materials, and some brands are only offered for 4/4 violins): one for 4/4 instruments, one for 3/4 and 1/2 instruments, and one for 1/4 and 1/8 instruments.
In the case of a cello, for the somewhat large size I give for a full-sized instrument of 759 mm for the body, the string length would be 703 mm in proportion, based on a string length of 690 mm for what is perhaps a more common full-size body length of 745 mm. And in the case of a double bass, the normal 3/4 size instrument with a body length of 1 metre and 110 mm would have a string length of 1 metre and 32 mm in proportion, based on one reference I have found.
Let's try to throw in string lengths, and include the viola, by arbitrarily setting the 17" viola to correspond to 3/4 size, as happened with the double bass, although, on the basis of a strict equivalency, one standard of comparison would be instead to treat the 14" viola as corresponding to 1/10 size, putting the sizes in the spot they approach most closely, and adjusting the string length to fit into this series:
Violin Viola Cello Bass
4/4, full size 355 mm (328) 759 mm (703)
7/8 345 mm (319) 737 mm (683)
3/4 335 mm (310) 17" (387) 716 mm (664) 1m 110 mm (1032)
5/8 326 mm (301) 16 1/2" (376) 696 mm (645)
1/2 316 mm (292) 16" (365) 676 mm (626) 1m 48 mm (974)
4/9 307 mm (284) 15 1/2" (353) 657 mm (608)
3/8 299 mm (276) 15" (342) 638 mm (591) 989 mm (919)
1/3 290 mm (268) 620 mm (574)
1/4 282 mm (260) 602 mm (558) 934 mm (868)
2/9 274 mm (253) 14" (319) 585 mm (542)
3/16 266 mm (246) 13 1/2" (308) 569 mm (527) 881 mm (819)
1/6 258 mm (239) 13" (296) 552 mm (512)
1/8 251 mm (232) 537 mm (497) 832 mm (773)
1/9 244 mm (225) 521 mm (483)
1/10 237 mm (219) 12" (273) 507 mm (469) 785 mm (730)
1/12 230 mm (213) 492 mm (456)
1/16 224 mm (207) 478 mm (443) 741 mm (689)
1/18 217 mm (201) 11" (251) 465 mm (430)
1/20 211 mm (195) 451 mm (418) 699 mm (650)
1/24 205 mm (189) 438 mm (406)
1/32 199 mm (184) 426 mm (395) 660 mm (614)
Most of the viola sizes don't fit too badly in their assigned spot, but the 14" viola is close to halfway between 1/4 and 2/9 size, so making it the basis for string lengths seems awkward, so instead of basing string length on position in the sequence, I've just derived it from the body dimension.
Of course, sizes should be scaled appropriately if one is starting from a 4/4 violin with a body length of 358 mm (14 1/8") instead of 355 mm (14"), or a 4/4 cello with a body length of 737 mm (29") or 749 mm (29 1/2") instead of 759 mm (29 7/8").
For comparison, the original body lengths of the instruments of the Violin Octet appear to have been:
Treble Violin 237 mm Soprano Violin 266 mm Mezzo Violin 383 mm (or, earlier, 405 mm) Alto Violin 511 mm Tenor Violin 646 mm Baritone Violin 859 mm Small Bass Violin 1m 37 mm Contrabass Violin 1m 278 mm
The sizes given on this page for violins and other related instruments are quoted in either inches or millimetres. But neither English units nor metric units were in use in the Cremona of Stradivari's day, so possibly expressing dimensions in terms of the units which he had used might avoid rounding errors. One place where this might be significant is in the case of the ratio between dimensions D and E, since this would affect the precise angle between the belly and back of the violin.
From the book Stradivari by Stewart Pollen, it is noted that a harp made by Stradivari has markings indicating that he used a Cremonese foot of 483 millimetres. Other sources give such a unit as well.
An official document, approved by a decree of May 20, 1877, Tavole di Raggulaglio de Pesi e Delle Misure Già in Uso Nella Varie Provincie del Regno col Peso Metrico Decimale gives the length of the "Trabucco di Cremona" as 2.901233 metres.
This leads to the following system of units:
Trabucco (6 Piede) 2.901 233 metres Piede (12 Once) 483.538 833 333 mm Oncia (12 Punti) 40.294 902 777 mm Punto (12 Atomi) 3.357 908 564 814 814 mm Atomo .279 825 713 734 567 901 234 567 901 234 567 mm
where the Piede is another name for the Braccio da Fabbrica, the unit in question, and the figures are prolonged sufficiently so the repeating decimals are visible without any claim to significance.
Of course, this was long after Stradivari's day, but it shows that the unit in question existed for long enough that a precise value was eventually established for it, to seven significant digits.
In Milan, the Atomo was further divided into twelve Momenti; in Piacenza, it was instead divided into twelve Minuti, each of which was divided into twelve Momenti, with each of those further divided into twelve Scrupoli, so this constitutes a duodecimal system of measurement. If we subject the Cremonese units to the Piacenzan mode of division (the Braccio in Piacenza was longer, 675 mm), we get:
Trabucco (6 Piede) 2.901 233 metres Piede (12 Once) 483.538 833 333 mm Oncia (12 Punti) 40.294 902 777 mm Punto (12 Atomi) 3.357 908 564 814 814 mm Atomo (12 Minuti) .279 825 713 734 567 901 234 567 901 234 567 mm Minuto (12 Momenti) .023 318 809 477 880 658 mm Momento (12 Scrupoli) .001 943 234 123 156 721 mm Scrupolo .000 161 936 176 929 726 794 695 930 498 mm
and so we would only have to repeat the division by 12 three more times to get a unit about the size of a nanometre, but we don't have to go any further to get into the realm of modern microelectronics; it wasn't that long ago that integrated circuits had feature sizes on the order of a Scrupola. A Scrupola is about 1.62 microns, and the original 80386 was made with a feature size of 1.5 microns.
Perhaps more significant for the history of the violin would be the units of measure used in Brescia.
However, here it is initially unclear which unit would have been used in woodworking. The possible units are:
Braccio da panno 674.124 mm Braccio da seta 640.383 mm Cavezzo 2.852 803 metres
The Braccio da panno is used to measure cloth; the Braccio da seta is used to measure silk. Both are divided into 12 Once.
The Cavezzo, like the Trabucco, is equal to 6 Piede, divided further into 12 Once per Piede, 12 Punti per Oncia, and 12 Atomi per Punto; it is the base of agrarian measure. For lack of any alternative, then, I think that the Cavezzo is the most likely unit of measure used for Brescian violins, and so the units of measure are:
Cavezzo (6 Piede) 2.852 803 metres Piede (12 Once) 475.467 166 666 mm Oncia (12 Punti) 39.622 263 888 mm Punto (12 Atomi) 3.301 855 324 074 074 mm Atomo .275 154 610 339 506 172 839 506 172 839 mm
However, a Braccio da fabbrica, although not given explicitly, is used in the definition of a unit of area; that is 475.467 mm; and that corresponds to 1/6 of the Cavezzo, confirming that it was used for making things, not just measuring land.
The Brescian measure is not that much different from the Cremonese measure; it is slightly shorter, about 59/60 of the Cremonese measure (a closer approximation is 3122/3175).
Incidentally, 3175 is, by an amazing coincidence, 25 times 127. This is an amazing coincidence because one inch is 2.54 centimetres, and 2.54 is 2 times 1.27. 3122 is 2 * 7 * 223, incidentally. But it isn't amazing enough to lead to a possibility to relate the ratio between these two measures to that between the inch and the centimetre in any simple way.
Yes, 1561 Cremonese Trabucci equal about 178,300.18555... inches (as well as, of course, being about equal to 1587 Brescian Cavezzi and 3 Brescian Piedi), while 625 Brescian Cavezzi equal 178,300.1875 centimetres, but that can be charitably described as underwhelming.
In terms of the marks one might make on a ruler, to have a smallest unit comparable to 1 mm or 1/16 inch in size, instead of stopping at the Punto, presumably each Punto should be divided into half, with marks representing six Atomi.
The effect of this on the shape of a violin can be significant. Take the example of Stradivari's 1720 violin given above, with a body 14 1/16 inches long/high, with the neck side 1 3/16 inches high/thick and the button side 1 1/4 inches high/thick.
In units of 1/16 of an inch, one has two heights of 19 units and 20 units, separated by a distance of 225 units; if the figure of the violin's ribs is a symmetrical wedge, then the two plates are tilted, in opposite directions, from the axis by the arctangent of 1/450, or about 0.1273 degrees.
Convert those measurements to millimetres, and round them to the nearest millimetre. Then the body is 357 mm long, the thickness at the neck is 30 mm, and the thickness at the button is 32 mm. Now, the plates would be tilted by an angle of the arctangent of 1/357, or about 0.1605 degrees.
If the actual dimensions of the violin were in units of 6 Atomi, about 1.68 mm, then we would have heights of 18 units and 19 units, separated by a distance of 213 units, so now the angle in question is the arctangent of 1/426, or about 0.1345 degrees.
What this really means, of course, is that measurements need to be made to a greater precision than one millimetre, whatever unit may be used, for the angles of the plates to be more than guesswork.
To improve the viola, Jean-Baptiste Vuillaume invented an instrument called the contralto. This instrument basically looked like a viola with its body split in half, with an additional rectangular piece inserted, thus making it wider without changing the shape of its sides. While the result was found to have a satisfactory tone, and the principle of its design was intended to make it possible to play it in a similar way to which the viola is played, the instrument was found to be unwieldy.
A more subtle redesign of the viola was proposed by Lionel Tertis, and Tertis pattern violas are offered by some makers. This widened the bottom part of the viola somewhat. Originally, it was intended to allow a 16 3/4" viola to sound similarly to a 17 1/8" viola, such as the 1717 Montagnana viola which was his preferred instrument.
Another approach, which I tend to favor, would be to avoid changing the shape of the viola, but simply increase its rib height, as is done with the cello, to make it more effective at lower pitches. One source states that this was done by Eugen Sprengner in 1930; he increased the rib height of the viola to 60 mm, or about 2 3/8"; another source notes that he also made the viola wider as well, but apparently only by a small amount, not making a radical change in its shape.
More recently, the Pellegrina was invented by David Rivinus in 1993 as a way to reduce the large size of the viola, thus helping to protect viola players from injuries such as carpal tunnel syndrome. The instrument has a somewhat unattractive appearance, looking like two left halves of a violin joined together, one upside down.
At first, I wondered if it might be possible to achieve the same thing with a shape like that of the contralto, but with the bridge, strings, and neck in an off-center position. On further consideration, in order to enlarge the instrument, but have everything reachable, while retaining a symmetric appearance, perhaps a solution would be to turn both sides of the instrument upside down, so that the smaller round part is nearer the player, which would then allow for the instrument to be widened as the contralto. Another option would be to thicken the instrument, as we will see below was done for the violoncello, except with a part at the bottom cut off so that a chin rest could still be used.
One very extreme expedient I came up with was to split the back of the instrument into two parts, with only the one further away from the performer increased in height. If only a small part of the back is associated with the smaller rib height, the fact that the sound post only communicates vibrations to the larger part of the back should not be a problem.
If instead, one were to divide the back in half, with a different rib height for each half, an arrangement such as that illustrated in this diagram could be used:
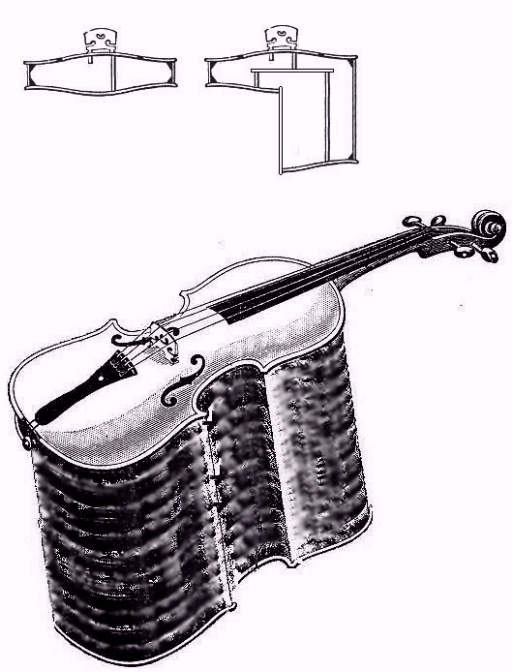
In this image, the instrument is divided between its left and right halves, but the division could also be between the top and bottom halves. The sound post is redesigned based on the idea that the lever connecting the one sound post from the belly to the two sound posts going to the back would appropriately split the motion from the belly between the two pieces of the back based on their stiffness.
One thing the diagram attempts to illustrate is that the thickness of the part of the instrument that is away from the performer could, presumably, be increased by quite a lot without getting in the way, with the floor presumably being the only obstacle.
This would allow even an instrument that the performer can handle as having a very small size to have a very large air volume. Of course, in extreme cases, the strings needed to have such low pitches at such short lengths under a reasonable tension would likely compromise the sound quality by their thickness, and so this should be avoided.
Inspired by the Pellegrina, the Tertis, and by Eugen Sprengner's design, as well as by the instruments of the Quartetto Futurista made by Ignio Sderci, I thought that a design less radical than the Pellegrina that would attempt to be as large as possible while retaining the string length and basic body size of the violin might look like this:

The diagram shows, for comparison, the ribs of a standard violin, and then the possibilities for extending them in three of the instrument's four quarters. In the upper left corner, a less radical and a more radical enlargement are shown.
In addition, if the goal is to make the instrument easier to play, reducing the size of the viola in the upper right corner, following the ergonomic viola of Otto Erdész, would seem advisable, and this is also shown in the diagram. While the idea was to reduce the general size of the viola to that of the violin, thus eliminating the need for such a measure, for one thing, it might be that in spite of every step taken to increase air volume, a string size and basic body length greater than that of the violin might still be needed, and, for another, simply because the modification may be needed more urgently in the case of the viola, even players of the violin - and, therefore, players of a violin-sized viola also - might benefit from help in reaching the higher hand positions.
The back and belly plates in this design are not increased in size nearly as much as those of the Pellegrina, and so, depending on which instrument is being reduced to what body size, it may be necessary to increase rib height as well. As a starting point, I thought I could perhaps go with the 60 mm thickness used by Eugen Sprengner. The violas of large pattern made by Stradivarius, which may actually have been tenors or contraltos, tuned an octave lower than the violin, had rib heights of up to 43 mm. However, I have learned that even the rib height of conventional violas may be uncomfortable for performers, so even 43 mm, never mind 60 mm, is apparently too large.
Originally, when I came up with this design, I didn't include the Erdész modification, and so I felt that to be ergonomic, any instrument, a normal (Alto) Viola or the larger Tenor Viola would have to be reduced to the body size and string length of a violin to be reasonable to play. This meant that the previous scheme, of splitting the back into two parts, so that part of the instrument could have an extreme rib height, could not be avoided.
But since the Erdész modification is successful in making a conventional 16 1/2" viola playable by players who suffer from an RSI, it appears that an instrument using the design shown here could still have a 16 1/2" body size, and be made equivalent to a 19" Tenor Viola, thus allowing a playable version of that instrument to exist. And a version of that design with a more modest increase of area could attempt to achieve the same goals as the Tertis viola, thus allowing the use of conventional viola strings.
And a 19"-equivalent instrument could be strung as a Tenor Viola, or it could be strung as a conventional viola - an Alto Viola. So there would be two possible ergonomic forms of the viola - one that sounds pretty much like existing violas that are a bit on the large size, say 17 1/2", and another that sounds like a "fixed" viola, adjusted to be fully suited to the range of notes it plays, like the Alto Violin from the Violin Octet.
A "fixed" tenor, on the other hand, would have to be played like a cello, and, indeed, would not differ much from one in size.
Even the standard 4/4 violin sometimes leads to RSI problems. If one goes to a 7/8 violin with a body length of 346 mm, the rib height would need to be increased to about 38 mm to compensate, but apparently this is within - and at the extreme limit of - the acceptable range (with, as noted above, even 43 mm being too thick). But thanks to the Erdész modification, reducing the violin to 7/8 size ceases to be a necessity.
The Violin Octet by Carleen Hutchins may be instructive in illustrating the ideal sizes of the various instruments. The Alto, which corresponds to the viola, is given a body length of 508 mm, and the Mezzo Violin, which corresponds to the violin, is given one of 383 mm; both are larger than the conventional instruments of 432 mm and 358 mm respectively. However, apparently the Mezzo Violin has a smaller rib height than the conventional violin.
As well, the Baritone Violin, which corresponds to the cello, has a body length of 866 mm but a rib height of 138 mm, while those of the conventional cello are 797 mm and 121 mm for the older large-pattern cellos, and for the smaller standard cello of today, 759 mm and 117 mm. These sizes are examples, as both large-pattern and small-pattern cellos vary somewhat.