Having looked at the main keyboard for a form of accordion that will seem strange and exotic to many, it seems only appropriate to look at the auxilliary keyboard found not only on the usual type of accordion, but also on the commonplace chord organ.
That keyboard, as found on the accordion, under the Stradella arrangement, has the following scheme:
Major 3rd Bb F C G D A E B F# C# G# D# A# Root Gb Db Ab Eb Bb F C G D A E B F# Major Gb Db Ab Eb Bb F C G D A E B F# Minor Gb Db Ab Eb Bb F C G D A E B F# Dominant 7th Gb Db Ab Eb Bb F C G D A E B F# Diminished 7th Gb Db Ab Eb Bb F C G D A E B F#
An accordion may extend this arrangement by, for example, three columns to the left and right. A chord organ, on the other hand, may only provide a small group of the buttons shown here, for example, corresponding only to the major chords and the minor chords.
When a chord organ does provide more rows of buttons, the rows may not have exactly the same function as those of the accordion. For example, the rows of buttons on early Hammond chord organs followed this scheme:
Major+6th Gb Db Ab Eb Bb F C G D A E B F# Ninth Gb Db Ab Eb Bb F C G D A E B F# Major Gb Db Ab Eb Bb F C G D A E B F# Minor Gb Db Ab Eb Bb F C G D A E B F# Diminished Gb Db Ab Eb Bb F C G D A E B F# Augmented Gb Db Ab Eb Bb F C G D A E B F# Minor 7th Gb Db Ab Eb Bb F C G D A E B F#
although the actual layout on the original Hammond chord organ was different: the columns for G flat and F sharp were omitted, and on that particular organ, the columns were vertical, and the rows sloped slightly upward. On most other chord organs, however, the rows are horizontal, and the columns are strongly sloped, following the pattern of an accordion, although perhaps not quite as strongly as on an accordion in some cases.
Persons skilled in the musical art will, no doubt, be shocked at the oversimplifications that will be contained in the next two paragraphs.
When playing music on a piano, a common pattern is that the right hand will play the melody, which is the part written on the treble staff, and the left hand will play the accompaniment, the part written on the bass staff. The melody will usually consist of one note at a time, and will tend to be played faster (well, both parts must be played in step, but the melody will have shorter notes in it) than the accompaniment. On the other hand, the accompaniment may involve the playing of three notes at once most of the time.
Playing piano sheet music as written is a skill which requires much practice. On the other hand, playing only the melody with the right hand is something that can be done tolerably well at a relatively early stage in learning to play the piano or another keyboard instrument.
Thus, the chord organ was devised as a way to allow someone whose musical skills were relatively limited to still play songs on the organ enriched by an accompaniment of sorts.
The first chord organ, by Hammond, was an electronic organ. Accordions make their sound through the use of small reeds; like a harmonica, one reed is required for the two possible directions in which air may travel - when the accordion is being stretched, and when it is being compressed. A reed organ, on the other hand, needs only one set of reeds. Since the idea of chord buttons came from the accordion, it is not surprising that many inexpensive reed organs also had chord buttons. (Today, of course, inexpensive keyboard instruments are made with microchips and not reeds, and if they do include a feature for playing a chord at the press of a single key, it is usually a switchable use of part of the regular piano keyboard.)
In chord organs using reeds, generally only one set of twelve reeds is provided to be operated by the chord buttons, and the range consists of one octave starting with C and ending with B. With an accordion, this is partly true as well, but an accordion may provide a set of stops with which to choose the registers used by the chord buttons.
Four of these registers extend from C to B:
The fifth register provided, the Contralto register, extends from the F# below middle C to the F above middle C.
However, surprisingly, the Tenor and Bass registers are only used by the two top rows of buttons, which produce a single note. Thus, the lowest register used for chords made by pressing a single chord buttonis the Contralto register.
A standard accordion has seven stops, which select the following combinations of the five registers:
Thus, to use only the lowest register possible for the chords, the Contralto register, one would select the Soft Bass stop.
An accordion may have only some of the five registers, and only some of the seven register buttons, listed above. On the side with the piano keyboard, there may also be register buttons, which serve the same function as the stops on an organ.
The typical registers on the right-hand side of an accordion will be a 4' register, an 8' register, and a 16' register, plus up to two other 8' registers, one tuned slightly above standard pitch, the other tuned slightly below standard pitch.
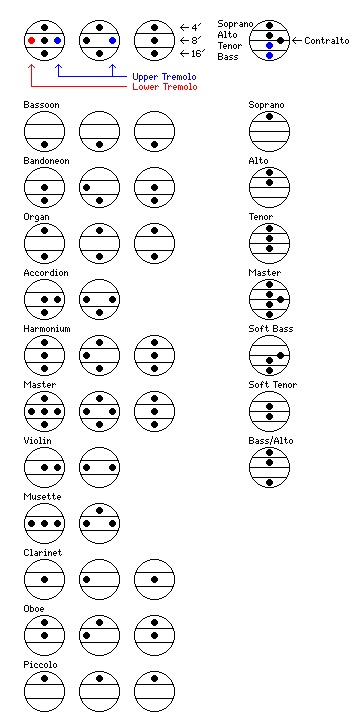
The register buttons on both sides of the accordion are indicated by symbols. On the left is an image showing the form of these symbols; first, on the left side of the diagram, is shown the form of the symbols for the register buttons on the right-hand side of the accordion in three cases - when the lower tremolo register, used primarily for the Musette sound, is present, when only the upper tremolo register is present, and when neither tremolo register is present.
On the right of the diagram are shown the symbols used for the register buttons associated with the chord buttons on the left-hand side of the accordion.
Thus, while a major chord consists normally of a given note (after which the chord is named; that is, if the note is C, the chord is the C major chord), the note four semitones above it, and the note seven semitones above it; or the note, the note a major third above it, and the note a perfect fifth above it; to keep within the twelve reeds available, it may be that one or both of the two higher notes of the chord will be lowered by an octave.
Incidentally, as any given reed may be called for by any of several chord buttons, the linkage is usually so arranged that if two or more buttons are pressed at once, the set of reeds that are allowed to sound is the logical OR of those called for by each of the buttons pressed. This allows chords other than those directly provided by an individual button to be played by pressing more than one button at a time.
As the notes of the chords are lowered by an octave in a fixed manner, guided only by the need to use only the twelve notes made available for chords, this means that considerations of what is called voice leading are ignored. Thus, the chord organ is not a full substitute for learning how to play a real organ, of course. But for those lacking the time or the skill to do that, it still serves a purpose, and by helping to produce more enjoyable music at an earlier stage in learning to play, it may even be credited with making the journey of those who seek to learn to play a keyboard instrument properly more pleasant along the way. As well, while there may be few recordings of chord organ music, accordion music is taken seriously enough that it has been recorded from time to time.
While some general comments about the social role fo the chord organ have been occasioned by explaining what it is, and how it works, they are, however, not the main purpose of this page. The circle (or line) of fifths has been met with in the first page of this section, as a way to order the notes of the octave based on the 3:2 ratio of frequencies, which is one of the strongest pleasant harmonies in music. It is because this important harmonic interval influenced the design of the diatonic scale that two keys a perfect fifth apart are also closely related in the sense that playing diatonic music in those two keys makes use of almost the same keys on the piano keyboard, except for one white key and one black key.
Thus, given that the chords are all composed of notes restricted to a single octave, thinking of them in circular rather than linear terms is natural for that reason, and because of the importance of the perfect fifth, chords starting on notes a perfect fifth apart are also related, in the sense of being more likely to occur together in the same piece of music. Thus, the arrangement of the columns of chord buttons by fifths reduces the back-and-forth movement along the chord keyboard of the performer's left hand.
It has been noted that a major chord, when in its normal form rather than an inversion, consists of a note, the note a major 3rd higher, and the note a perfect 5th higher. Therefore, from this table which also appeared on the first page of this section:
Name: Frequency Distance in Distance on
ratio: semitones: the 53-unit scale:
Unison 1:1 0 0
Minor second 16:15 1 5
Major second 9:8 2 9
Minor third 6:5 3 14
Major third 5:4 4 17
Perfect fourth 4:3 5 22
Augmented fourth 45:32 or 25:18 6 26 or 25
Diminished fifth 64:45 or 36:25 6 28 or 29
Perfect fifth 3:2 7 31
Minor sixth 8:5 8 36
Major sixth 5:3 9 39
Minor seventh 16:9 10 44
Major seventh 15:8 11 48
Octave 2:1 12 53
we can see that the nominal frequencies of these notes are in a 4:5:6 ratio, a major third having the 4:5 frequency ratio, and a perfect fifth a 2:3, and therefore 4:6, ratio.
If we invert the chord by lowering the highest note an octave, the ratio of frequencies becomes 3:4:5, illustrating even more clearly that this chord is highly consonant, based on a very simple ratio between the frequencies of the notes involved.
In a minor chord, the notes present consist of the root of the chord, the note a minor third above that, or three semitones above, and again the note a perfect fifth above the root.
In this case, the frequencies of the three notes in the chord are, at least nominally, in a 10:12:15 ratio. This is still highly consonant, if not as much so as the major chord.
Most of the triads that can be formed by the notes of the diatonic scale are either major chords or minor chords:
VII * * *
VI 10 12 15
V 4 5 6
IV 4 5 6
III 10 12 15
II * * *
I 4 5 6
24 27 30 32 36 40 45 48 54 60 64
Do Re Mi Fa So La Ti Do Re Mi Fa
C D E F G A B C D E F
If we lower the frequency of D by a syntonic comma, so that D is now at 10/9 of the frequency of C rather than 9/8 of that frequency, we get this chart, in which the ratios are visible for the triad starting from D:
VII 25 30 36
VI 10 12 15
V * * *
IV 4 5 6
III 10 12 15
II 10 12 15
I 4 5 6
72 80 90 96 108 120 135 144 160 180 192
Do Re Mi Fa So La Ti Do Re Mi Fa
C D E F G A B C D E F
The triad beginning with B, however, consists of B, D, which is a minor third above B, and F, which is a diminished fifth above B. This is a diminished chord, and it is less consonant than the minor chord. Usually, when it appears in music, it is quickly resolved to a more consonant chord; that is, the next chord appearing will be a more consonant one, giving the impression of a tension being relieved; a satisfying happy ending, as it were.
For purposes of playing music, a major chord is a major chord; the C major chord is a C major chord, whether it is being played in a piece of music in the key of C, or in a piece of music in the key of F. When writing music, the relationship of a given chord to the diatonic scale in use is important for understanding such things as chord progressions; thus, the different chords built on the notes of the diatonic scale are designated by Roman numerals, as appear on the left of the tables above.
When Harlan Howard made his famous remark that "All you need to write a country song is three chords and the truth", the three chords referenced would usually be I, IV, and V - for a song in the key of C, the C major, F major, and G major triads.
Given that in the tables above, the need for D as 10/9 instead of 9/8 only arose when we considered the minor triad, if the simplest popular music uses only the three major triads, it may be of interest to ask if there might be a way to assign a single pitch to each of the twelve notes in the octave to allow just intonation under suitably restricted conditions.
Assume that the melodies used are diatonic, and the chord relations involve only the three major triads of I, IV, and V. Also, however, allow the key to modulate by a fifth and back again - at least that simplest of modulations usually does take place in popular songs.
Also, considerations of vocal range affect the keys that will be used. Thus, a melody that modulates upwards by a fifth at one point may need to go from the key of F to the key of C instead of from the key of C to the key of G. F and G being separated only by a whole tone, we can, however, assume that a wider range of keys is not really needed.
However, the answer is no. Even in popular music as simple as this, the syntonic comma is required for just intonation. If you go from the key of C to the key of F, the diatonic scale now includes the D of 10/9 instead of the D of 9/8. If you go from the key of C to the key of G, the diatonic scale now includes the A of 27/16 instead of the A of 5/3. Thus, although you are only using two of the five black keys on the keyboard - F sharp at 45/32, and B flat at 16/9 - two of the white keys already have to have two different values.
Modulating downwards a major third, on the other hand, lets one use the existing G, C, and F, and all the new notes required for the diatonic scale are on black keys. But that is a relatively exotic key, with four flats, and thus the point that the conflict between equal temperament (or any assignment of fixed pitches for the twelve degrees of the scale) and just intonation arises at a very early point in music stands.
A simple chart can show the types of triad we have met so far, as well as the other common ones, in terms of semitones:
Major ninth (major second + octave) 14
Minor ninth (minor second + octave) 13
Octave 12
Major seventh 11
Minor seventh 10 * *
Major sixth/Diminished seventh 9 * *
Augmented fifth/Minor sixth 8 *
Perfect fifth 7 * * * * *
Augmented fourth/Diminished fifth 6 * *
Augmented third/Perfect fourth 5
Major third 4 * * * *
Minor third 3 * * * *
Major second/Diminished third 2
Minor second 1
Root * * * * * * * *
Major Minor Dim. Dom. Minor Major Aug. Dim.
7th 7th +6th 7th
The chord of the Dominant 7th can only be formed from G, B, D, and F when only the white keys of the piano are used; thus, its root note is "So", or the Dominant, when made from notes native to the diatonic scale in use; therefore, it unambiguously gives a definite feeling of the key, or unambiguously indicates the tonic. This chord is also designated, in the Roman numeral notation, as the V7 chord, and it is sometimes used in popular songs that are otherwise based only on the basic I, IV, and V chords. The three minor triads, and the diminished triad, within the diatonic scale are the secondary triads, with the three major triads being the three primary triads. However, when music is in a minor key, then the I, IV, and V triads are still the primary triads, although now all three start out as minor chords.
The augmented triad, and the diminished 7th chord can only be made using accidentals (sharps, flats, or naturals outside the current key signature). The augmented triad consists of three notes, at equal spacings of four semitones, and the diminished seventh chord consists of four notes, at equal spacings of three semitones. Thus, both of these chords consist of a complete set of equally-spaced notes from among the twelve notes in the octave, and therefore are often used when a composition is to switch from being in one key to another key (modulation) when those keys are remote. (The distance between keys is in terms of the circle of fifths; since only one note on the scale is changed when the key is moved up or down by a fifth, special chords like these are not needed for that much more routine type of modulation.)