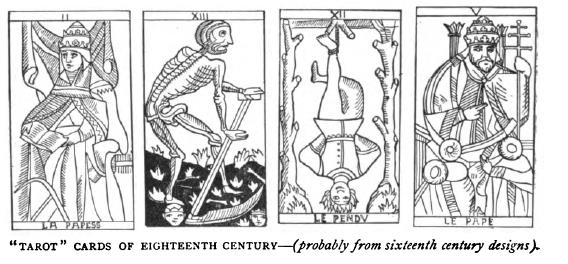
Just as ordinary playing cards come in many different styles, the same is true of Tarot cards.
The traditional form of those cards is shown in decks ranging from the Tarot of Marseilles to the 1JJ Tarot. An example of such cards is shown below, in an illustration from an old magazine:

Tarot cards intended for card games have, in some countries, had the pictures associated with the trump cards completely replaced. One example of a card in this style is shown below:

Starting in the 1960s, however, one particular Tarot deck, designed in 1909, became so popular as to eclipse nearly all other styles, at least in North America, where the Tarot was almost exclusively used for fortune-telling as opposed to the playing of card games, as to define what the Tarot should look like.
It wasn't a traditional deck like the Tarot of Marseilles, although that one was also available:

Nor was it the fortune-telling Tarot designed by Etteilla, also available as well:

No, it was this one:

Recently, some books have been published giving more information about the story of how this deck, the popular Rider-Waite Tarot deck, came to be. They have included a picture of Pamela Colman Smith, and, as well, noted its original public-domain source, which happens to be online: an article in the October, 1912 issue of The Craftsman, volume 23, number 1, titled The Fairy Faith and Pictured Music of Pamela Colman Smith, written by M. Irwin MacDonald.
On subsequent pages, though, the article is just headed "A Painter Who Sees Fairies".
Here, then, I give that picture, plus an image of a different drawing of Ellen Terry, leading lady in Henry Irving's Shakespearian company, than the one which those books reproduced to show that I went to the original well for my image.
And, subsequently, I also show a photograph of Arthur Edward Waite; this one appeared in Strange Houses of Sleep, a volume of his poetry from 1906.



Thus, to prove my journey, I brought back "the Tiger's fang", as one Paul Twitchell claimed to have done in another context.
Incidentally, I did enhance the contrast of the photograph in a paint program; my source was the printed page, not an original photographic print, despte appearances! My clumsy efforts to do the same for the image of Waite, originally of a sepia cast, have given it a greenish tint.
Of the Rider-Waite Tarot deck for which she supplied the drawings, the noted author Arthur Machen wrote (in the April 15, 1910 edition of T. P.'s Weekly):
"And with [The Pictorial Key to the Tarot] comes the most wonderful pack of cards that has ever been seen since the days when Gringonneur illuminated three packs for the amusement of King Charles VI of France in the year of our Lord 1392."
The Rider-Waite Tarot was first advertised for sale in late 1909, and it continued to be advertised until 1920. The University Press edition of that deck appears to have first become available in 1959, while it began being published by its current publisher, U.S. Games Systems, in 1970. There was also the more colorful Albano-Waite edition from 1968. Zolar's Astrological Tarot, which used the designs from this deck, was first sold starting in 1963.
I note this chronological information to exculpate the free enterprise system somewhat. Pamela Colman Smith recieved a one-time payment, without royalties, for her work on Waite's Tarot deck. However, as she died in poverty in 1951, rather than, say, 1981, there would not have been much in the way of royalties to speak of in any case; it was in the 1960s and especially the 1970s that sales of the Rider-Waite deck started to mushroom, and for her to be in poverty while that happened would, of course, have been a glaring injustice. Of course, her fate is still sad and regrettable, but in 1951, the stark contrast that seems to be percieved would not yet have existed.
However, I have learned that it would have been possible to purchase a deck with the designs drawn by Pamela Colman Smith in 1951. In FATE Magazine, and similar places, for many years one might have noted advertisements for "The Great Book of Magical Art, Hindu Magic and Indian Occultism", by L. W. de Laurence. Well, his firm began publishing an apparently pirated version of the Rider-Waite Tarot in 1916, and continued to do so right up until 1980.
And, as well, at least in Britain, Rider & Company were still publishing this deck until at least 1977, although by 1977, they appear to have simply bought decks from U.S. Games Systems - and there may well have been an interregnum of limited demand. The version of the Rider deck known as Pamela A was the one published until 1920; Pamela C was the next version published, with Pamela B following. Pamela D was the final version, reproduced photographically from Pamela A, whereas the two other versions were redrawn, with a few minor differences.
From Wikipedia, I learned that her mother was the sister of the American painter Samuel Colman, and that her father was the son of Cyrus Porter Smith, a mayor of Brooklyn. I mentioned this in preparation for an attempt to address a sensitive point which I have since found is fully and logically addressed here in a logical, if not absolutely decisive, manner.
Apparently, L. W. de Laurence was able to get away with publishing a pirated version of this Tarot deck in the United States because Rider & Company had neglected to take the necessary steps to secure their copyright in the United States. Since the deck was originally published in Britain, however, in the rest of the world its copyright followed what was already the established practice for copyright: 95 years after publication for institutional works, or 70 years after the death of the author.
Thus, it was not in the public domain, as an American work would be, because of having been published before 1923. A. E. Waite died in 1942, prior to Pamela C. Smith, and so the deck remained under copyright up to the year 2021. U.S. Games Systems is still protecting the deck to the extent it can, with its name, the "Rider-Waite Tarot" being a trademark.
Another indication that some people had an interest in Tarot cards before 1951, and also outside the United States, where it would have made a difference to her financially, is that in 1935, a British women's magazine, My Weekly, commissioned a set of Tarot cards that was made available to readers as an advertising premium. This set was done by a different artist in a different style, but the designs of many (although not all) the cards in it were based on those in Pamela Colman Smith's deck. This deck is known as the Thomson-Leng deck, that being the name of the magazine's publisher.
Incidentally, Thomson and Leng are not an obscure publisher. They produced the well-known annual The Friendship Book, and they are responsible also for the popular British comics Oor Wullie and the British version of Dennis the Menace.
It is an interesting story how Hank Ketcham in the U.S. and David Law in Britain created two very different comic characters which were first published on the same day, March 12, 1951. The American one is blond and innocently mischevious, while the British one is dark haired and a bully.
Incidentally, specialized decks of fortune-telling cards have, of course, been produced in many different sizes. However, there is a "tarot" size of playing cards, and I do remember that the cards in one of the University Press decks that I once had were quite large, and so I believe that the original cards published by Rider & Co. were in fact in that size.
This schematic diagram gives a comparative illustration of the size of three different types of playing card; Bridge size, Poker size, and Tarot size.
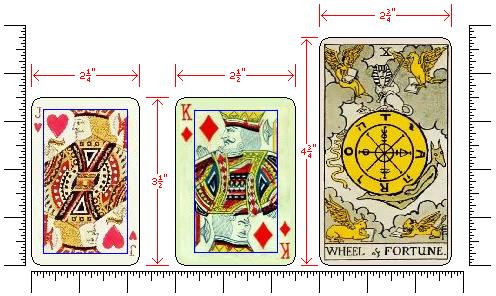
The cards are accompanied by a scale like that of an inch ruler, from which it can be seen that a Bridge size card is 2 1/4 by 3 1/2 inches, a Poker size card is 2 1/2 by 3 1/2 inches, and a Tarot size card is 2 3/4 by 4 3/4 inches.
Thus, the ratio of width to height for these three types of card are 9:14, 5:7, and 11:19 respectively, making the width 64.29%, 71.43%, and 57.89% of the height, approximately, in the three cases, from which we can note that the Tarot size of card is the narrowest of the three; fortunately, however, if it is desired to print Tarot cards at a smaller size, there will be little waste if the standard Bridge size of card is used.
Amazingly, the 56 cards of Zolar's Astrological Tarot Fortune-Telling Cards, despite being limited in number to something comparable to the number of cards in a standard deck of cards, were also, at least originally, of Tarot size.
It is possible, of course, to get a miniature version of the Rider-Waite Tarot cards; these cards are 1 3/4" by 2 7/8", for a ratio of width to height of 14:23, making the width 60.87% of the height, very close to that of the Tarot size of card. Miniature playing cards, on the other hand, are usually 2 1/2" high.
As well, a pocket-size version, and a giant-size version, are offered.
The size of the regular cards, which I have given as 2 3/4 by 4 3/4 inches, is also quoted elsewhere as a slightly less tall 2.75 by 4.72 inches, or a metric 7 cm by 12 cm.
I had to dig a bit further to get the size for the pocket edition cards: 2 1/4" by 3 1/2", the same as standard Bridge size.
The size I first saw quoted for the giant-size deck is metric, 10 cm by 17.5 cm, but when I dug down to the original source for the pocket edition, I also got the size of 4" by 6 1/2" for the giant-size cards; this gives a ratio of width to height of 8 to 13, making the width 61.54% of the height, again appropriate for Tarots.
And this is the closest approach yet to having the width about 61.8% of the height, which is the shape a playing card would have if its proportions were determined by the Golden Ratio ( (1+sqrt(5))/2, or 1.618033988749894848... ).
Speaking of playing cards, after a History Channel documentary filmed on the premises of the U.S. Playing Card Company was brought to my attention, since it was stated that the opaque black paste used to bind the two layers of a playing card together by them was a closely guarded secret, I did a web search, and came up with U.S. Patent 1,811,322 by three inventors, one from Austria and two from Germany, for the formula of an adhesive which would meet that requirement. Of course, the U.S. Playing Card Company could have either improved this formula, or they could be using their own formula of a different nature. One requirement that is more severe today than back in 1930 would be that only nontoxic substances should be used.
Further searching has turned up the fact that this kind of adhesive in general is referred to in the trade as "block-out glue" or "stop light glue", and one company that is a supplier of it is L. D. Davis Glues and Gelatins. Sierra Coating Technologies also supplies block-out glue, but their web-page seems to suggest that they supply it chiefly for making signage, with playing cards only mentioned as a historical application.
On the other hand, it is noted in Scarne's Complete Guide to Gambling that the black paste joining the two layers of pasteboard in a playing card together is called "gook"; whether (or, for that matter, if) this name fell into disuse because of its use as a racial slur, or simply the potential for confusion is a matter on which I am at this time unable to shed any light.
More material about playing cards is on this page. That page deals with how the composition of the sets of cards made available for different sets of cards for the Magic: the Gathering collectable card game were affected by the constraints of how playing cards are printed.
Basically, since an ordinary deck of playing cards will usually contain:
for a total of 55 cards, and the height of a Bridge sized playing card is the same as that of a Poker sized playing card at 3 1/2 inches, playing cards are usually printed from rolls of card stock that are 38 1/2 inches wide (plus some extra allowance for space between the cards when they're punched out with dies in cookie-cutter fashion to ensure each card is identical).
The Tarot-sized card fits in, but oriented in a perpendicular direction, because its width, being 2 3/4 inches, is exactly 11 times 1/4 of an inch, so fourteen of them would be 38 1/2 inches across.
How would the miniature Tarot cards, 1 3/4" by 2 7/8", fit in? As the 1 3/4" width of these cards is exactly half of the 3 1/2" height of a standard playing card, whether Bridge size or Poker size, 22 such cards across would fit in the 38 1/2" dimensional constraint.
The giant-size cards at 4" by 6 1/2", though, don't seem to fit in an obvious and simple way. However, if you subtract 6 1/2 from 38 1/2, you get 32, which divides by 4, so you could accept a little wasted cardboard, and base your layout on having eight columns of cards standing up, and one column of cards lying down.
And eight rows of cards standing up would be the same height as a column of thirteen cards lying down, so one could avoid wasted space by printing sheets of 77 giant-size cards. However, such sheets are likely to be too large for the presses normally in use.
Here is a diagram showing several of the sizes of cards discussed, and how they would fit.
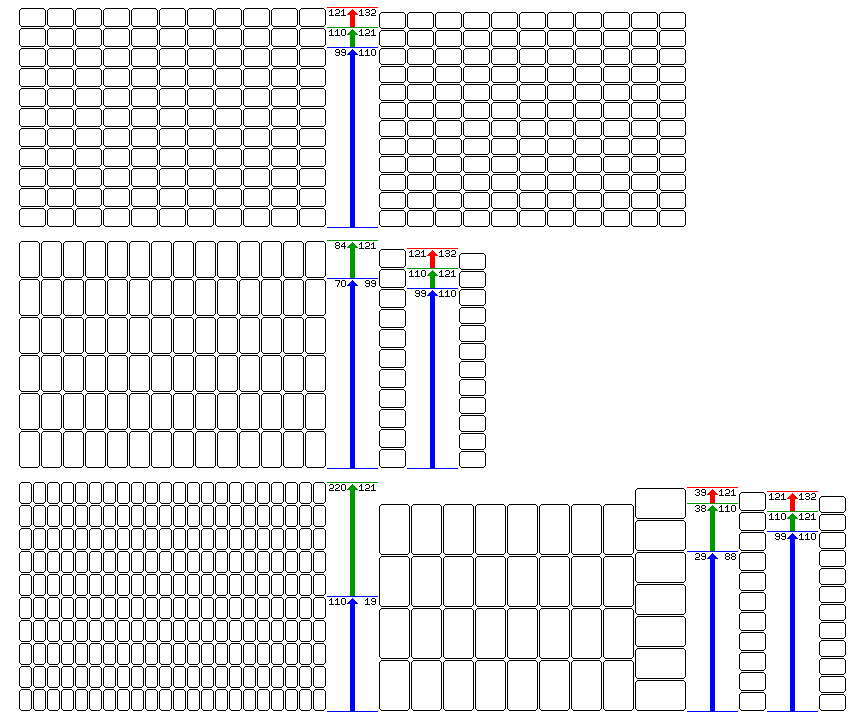
On the top, we see a comparison between Poker size cards on the left, and Bridge size cards on the right. 99 Poker size cards would occupy a sheet exactly the same size as 110 Bridge size cards. However, rather than using the same size sheet for both, using a proportionately larger sheet for Poker size cards keeps things simple, allowing one to print two packs of cards on a sheet in both cases.
The second line shows Tarot size cards, with the heights of the sheets for Poker size and Bridge size cards shown on the right. While the Tarot size of card certainly does fit exactly on sheets with the standard width, in the same size range as used for printing regular playing cards, it's hard to find a size of sheet that relates well to the number of cards needed for a pack.
However, if you use 70 card sheets, and include two extra cards in a Tarot pack of 78, using one sheet for 70 of the cards, and another sheet for the remaining 10 cards, repeated seven times, is simple enough.
The third line, on the bottom, shows miniature Tarot cards on the left, and giant-sized Tarot cards on the right.
It's very easy to make a multiple of 55 cards on a sheet. Since a Tarot pack of 78 cards is equivalent to one and a half packs of 52 conventional cards, a sheet size that is good for conventional cards is also good for Tarot cards.
What about the giant-sized Tarot cards? Let's pick a sheet with 38 cards on it as the most efficient and convenient size of sheet to print.
Twice 38 is 76, which is just two short of the number needed for a pack. So one could produce Tarot decks this way:
One sheet has the first 38 cards, a second sheet has the second 38 cards, and a third sheet has the remaining two cards, repeated 19 times. A fourth sheet, with, for example, two extra cards per deck repeated 19 times would avoid wasting any cards, instead of having one sheet with four cards repeated nine times, or three cards repeated six times.
A few other sizes of cards can be mentioned that also fit into this scheme.
Domino size cards are half as wide as they are tall, being 1 3/4" by 3 1/2"; having the same height as ordinary playing cards, it's clear they'll fit nicely on a sheet lying down.
Square cards, 3 1/2" by 3 1/2", are another commonly available size.
Miniature playing cards can be 1 3/4" by 2 1/2". Since 1 3/4" is exactly half of 3 1/2", they would fit on the sheet standing up. These cards are exactly 70% as wide as they are high, while Poker size playing cards, at 2 1/2" by 3 1/2" are 71.43% as wide as they are high. Clearly, just as Bridge size and Tarot size cards approximate the Golden Ratio, Poker size cards approximate the square root of 2.
Other sizes of miniature playing cards exist. I have recently acquired for my collection a set of miniature playing cards published by Goodall & Co. which are 1 3/4" by 2 5/8" in size.
Actually, though, there is a good reason why the ratio between the height and the width of a sheet of paper might be close to the square root of 2, but this reason does not apply to the Golden Ratio.
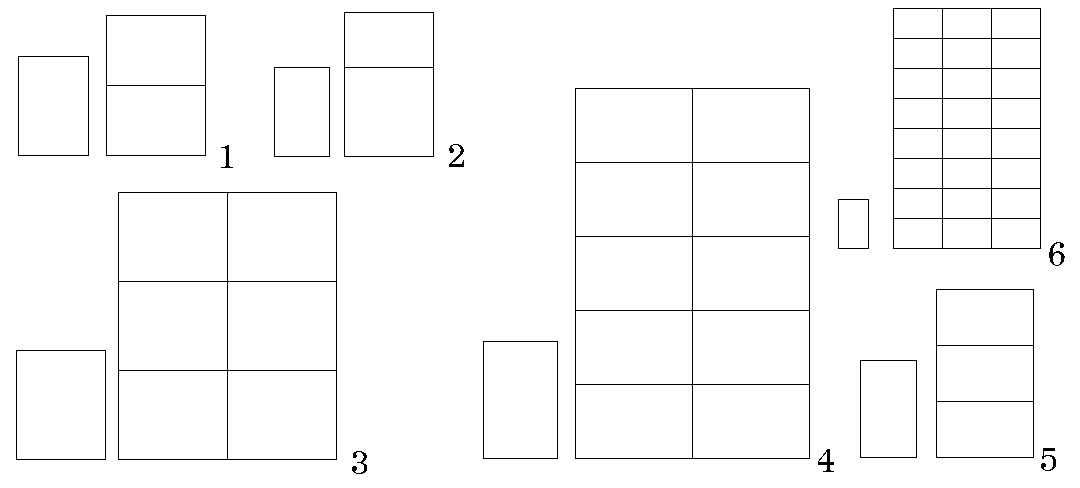
In the diagram above, we see in section 1 that a rectangle with sides in the ratio of 1 to the square root of 2 can be cut in half in the middle to make two rectangles of the same shape.
This makes sheets of paper in that shape practical for printers, since it gives them more choices; in addition to cutting a large sheet of paper of that shape into 4, 9, 16, 25, 36 and so on sheets of paper, also of that shape, they can also cut such a sheet into 8, 18, 32, 50 and so on sheets of paper of that shape.
And I have found out from Wikipedia that it is even known who came up with this idea: one Georg Christoph Lichtenberg first suggested it in 1786.
With the Golden Ratio, on the other hand, as shown in section 2 of the diagram, a rectangle with sides in that ratio can be cut into a smaller rectangle with sides in that ratio... plus a square. So that doesn't do anything for printers.
However, other square roots can work the same way for printers.
Thus, let's go to section 5 of the diagram. A rectangle with sides in the ratio of 1 to the square root of 3 can be cut into three rectangles of the same shape. So now a large sheet in that shape, in addition to being able to be cut into 4, 9, 16, 25, 36 and so on sheets of the same shape, can be cut into 12, 27, 48 and so on sheets of the same shape, again giving the printer more choices.
Section 3 of the diagram shows how this would also work if the aspect ratio of our sheet of paper is based on the square root of 1 1/2, and Section 4 of the diagram shows how it works for an aspect ratio based on the square root of 2 1/2.
The square root of 2 1/2 is 1.58113883..., and so it might be a possible choice if one is looking, for aesthetic reasons, for something close to the Golden Ratio. The square root of 3 is 1.7320508..., so that approaches it from the other side.
Section 6 of the diagram looks at the square root of a number between 2 1/2 and 3, in order to get even closer to the Golden Ratio: the square root of 2 2/3.
The square root of 2 2/3 is 1.632993161855452... which is quite a close approach to the Golden Ratio. However, this shape of rectangle gives us the choice of cutting a large sheet in this shape into 24 pieces of the same aspect ratio, and, of course, we already had the choice of cutting it into the square number of 25 pieces of the same aspect ratio. So does this alternative really add something new?
Well, if we're also constrained to use round numbers and not just rational ones, it may be easier to cut a sheet of paper into 9, 16, and 24 parts instead of 9, 16, and 25 parts, if we use a unit divisible by 3 and 4, while being spared the need to make the basic unit also divisible by 5.
Also, if we aren't concerned about using only small numbers, then by repeating the process, we might be able to obtain a finely graded series including a large number of choices.
Remember, too, that we aren't using card dimensions involving exact square roots. So instead of having cards of different sizes with exactly the same aspect ratios, we're simply having cards of different sizes which have aspect ratios that are close to one another.
Looking at the various card sizes we've seen so far with an aspect ratio close to the Golden Ratio:
Miniature Tarot 1 3/4" by 2 7/8" (14:23, 60.87%) Bridge Size 2 1/4" by 3 1/2" (9:14, 64.29%) Tarot Size 2 3/4" by 4 3/4" (11:19, 57.89%) Giant-Size Tarot 4" by 6 1/2" (8:13, 61.54%)
is it possible to fit several of these sizes on the same size of sheet, and if so, does the size of the sheet, and the layout of cards on it, reflect the sqrt(2 2/3) approximation to the Golden Ratio, or something else?
The Bridge Size and the Miniature Tarot size are in harmony, as the width of the Miniature Tarot, at 1 3/4", is exactly half of the height of the Bridge Size at 3 1/2". So when will the other dimensiions of these two card sizes come into coincidence?
The height of a Miniature Tarot size card is 2 7/8", so that is 23/8", while the width of a Bridge size card is 2 1/4", or 18/8". The least common multiple of these two lengths would be 51 3/4".
And we already know that eleven times the height of a Bridge size card is the same as fourteen times the width of a Tarot size card; in the other direction, ten times the height of a Tarot size card would be nineteen times the width of a Bridge size card, so that would also involve a large sheet as the dimension involved is 47 1/2".
Thus, these sizes of cards do not appear to have been designed around a single size of sheet, even if they fit well to the standard width of the roll used for printing playing cards in large batches.
Since the width of a Bridge size card is 9/4", divisible by three, though, let's try making a sheet corresponding to eight Bridge size cards standing up across, and three Bridge size card heights in the other direction.
Such a sheet could be divided into nine cards lying down with dimensions of 3 1/2" by 6" high, or sixteen cards lying down with dimensions of 2 5/8" wide by 4 1/2" wide, an aspect ratio of 7:12, or 58.33% as wide as high. This is narrower than most of the types of cards considered here, but it's wider than the Tarot size of card, as well as being very close to it in aspect ratio, so it is potentially practical to use this ratio to print standard Bridge size cards, cards in a slightly smaller size similar to Tarot size cards at 2 5/8" by 4 1/2", and a Jumbo-sized Tarot card at 3 1/2" by 6", and even a slightly taller Miniature Tarot card at 1 3/4" by 3".
In practice, though, if one were trying to pick out a size for a sheet of cardboard from which to print playing cards, it would be vital to produce both standard-sized Bridge size playing cards and standard-sized Poker size playing cards. They both have the same height, at 3 1/2"; ten times the width of a Bridge size playing card at 2 1/4" equals nine times the width of a Poker size playing card at 2 1/2". So one dimension of such a sheet would be 22 1/2", and the other would be some multiple of 3 1/2". Assuming it is also desired to print standard-sized Tarot cards at 2 3/4" by 4 3/4" with minimal waste, what would be a good arrangement?
One place to start from would be to build 22 1/2" from a certain number of Tarot cards standing up, and another number of them lying down. Two standing up are 5 1/2" wide, two lying down are 9 1/2" long, and one of each are 7 1/2" in size. 15 plus 7 is 22, so the Diophantine equation has a simple solution, three standing up, and three lying down.
As it turns out, it's not until one gets to eleven times the 3 1/2" height of a Bridge size or Poker size card that one gets a height with no waste for those common sizes, and only a little waste for the Tarot size cards. The other two reasonably good sizes for a sheet involve a small amount of waste for the Bridge and Poker size cards as well.
What if we try our alternate size for Tarot cards of 2 5/8" by 4 1/2" instead?

In that case, if we choose a sheet that is 22 1/2" wide by 17 1/2" high, in addition to being able to print 50 Bridge size cards with no waste, and 45 Poker size cards with no waste, we are able to print 30 of these slightly smaller Tarot size cards with only a little waste, and 27 standard-size Tarot size cards with a bit more waste, so that would be a versatile size of sheet for more modestly sized presses.
While American Demy is 22" by 17", and the British Demy of which I had previously been aware was 19 1/2" by 15 1/4", there is an Imperial Demy which is 22 1/2" by 17 1/2"; could this have contributed to the origin of some playing card sizes?
Jumbo playing cards are 3 1/2" by 5 1/2", 63.64% as wide as they are high. With a width that matches the height of Bridge or Poker size cards, they're easy to fit standing up on a sheet, unlike the giant-size Tarot cards we saw above.
So far, I've only mentioned card sizes quoted in inches. And I've completely ignored the fact that, since the cards are punched out with dies, there needs to be some space between the cards. Since there would be more spaces between cards when there are more cards, the smaller-sized cards would have to be... even smaller... to fit on a sheet that only had enough extra space on it for the smaller number of spaces required between larger cards, because there are fewer of them!
To address card sizes quoted in metric, which don't correspond to round numbers in inches, first: 38 1/2" is just under 978 millimetres. Some metric sizes I've seen quoted are: 56 mm by 87 mm for U.S. games, 63 mm by 88 mm for European Poker cards, 62 mm by 100 mm for Trump size cards, 44 mm by 67 mm for European miniature cards, and 58.9 mm by 90.9 mm for Skat size cards (which is about 2 5/16" by 3 9/16").
Note that while Skat size cards may be noticeably larger than European bridge size cards, they're only about 1/16" larger in each direction than U.S. Bridge size cards, at 2 1/4" by 3 1/2". Attempting to fit this size of card to old sizes of the foot used in Germany or Austria initially yielded inconclusive results, but then in general it appears that sizes of playing cards derive more from what can fit on a sheet conveniently than from any historical standard.
One way to make everything fit nicely would be to assume metric cards are made on a printer that takes slightly wider rolls of card stock. Let the card stock be 1,008 mm wide.
56 millimetres would go into that 18 times, and 63 millimetres would go into that 16 times.
Divide it into 11 parts, and they would be about 91.63 millimetres, a bit more than is needed for Skat size cards. Can I come up with a width that will fit more of the possibilities?
A width of 616 mm would be 11 times 56 mm, and 7 times 88 mm, but it doesn't seem to cover more of these metric card sizes.
Looking elsewhere, I've seen a European bridge size given as 57 mm by 87 mm, Skat size rounded up to 59 mm by 91 mm, a Spanish card size of 62 mm by 95 mm.
3 1/2" is 88.9 mm, so European poker size is less tall than that, and European bridge size less tall by a slightly larger amount. That discrepancy suggests that metric cards are printed following a completely different scheme than that used for the inch sizes, although there's definitely a temptation to just use the space between cards to account for everything.
The Tarot size of card is quoted as 70 mm by 121 mm in metric, and 7 mm and 11 mm feature prominently in the other metric sizes, so just perhaps there is a system to be found after all.
Fourteen metric Tarot cards across would be 980 mm, only slightly larger than the size of roll for cards in inch sizes.
On the other hand, eleven European poker cards lying down are 968 mm. A pair of European poker cards standing up are 126 mm, which is 38 mm greater than 88 mm; so ten European poker cards lying down and two European poker cards standing up are 1,006 mm, so there's no way to get to exactly 980 mm by that route, it would seem. Ah, but perhaps the difference would be smaller if we went with nine European poker cards lying down, and three European poker cards standing up; that amounts to 981 mm, and so this could be our answer.
Can we use this roll width to explain why European Bridge size cards have to be 1 mm less tall?
Well, ten European Bridge size cards lying down plus two European Bridge size cards standing up add up to 984 mm. Perhaps we are on the trail of something.
Can Skat sized cards be made to fit? Well, fifteen Skat cards standing up plus one Skat card lying down is 974.4 mm, which could already be taken as close enough. Twelve Skat cards standing up plus three Skat cards lying down, however, is more likely the right answer, at 979.5 mm. However, nine Skat cards standing up plus five Skat cards lying down is 984.6 mm, which is even closer.
All this, of course, is just considering the large companies that mass-produce the most common decks of playing cards. Companies that do custom printing of playing cards will use smaller-sized printing presses, which will involve different calculations for card size.
Thus, for example,
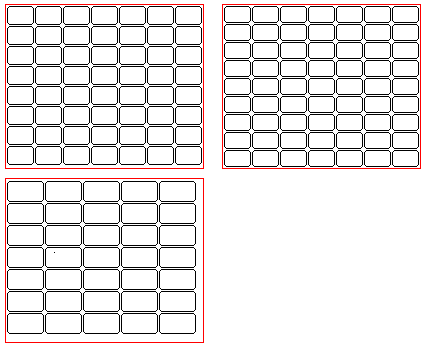
the illustration above shows a sheet with enough room for 56 Poker size cards, 63 Bridge size cards, and 35 Tarot size cards, which is about the size of what might be offered in such a case, although it's quite possible that they would have to make do with a size standardized for other purposes, which is not such a good fit.
But let's assume that one actually has this particular size of paper to deal with, and one wants to produce conventional decks of Bridge size playing cards.
One way to do that, of course, is to print one set per sheet, and just waste the extra cards.
A way to do better with only two sets of printing plates might be this: one sheet would have 31 cards printed twice, with one wasted card, and the other sheet would have 21 cards printed three times. That, however, produces decks of 52 cards with no jokers.
So a third sheet, with two extra cards repeated 31 times, or three extra cards repeated 21 times, would also be needed.
Could we improve this a bit, by not wasting the extra card on the first sheet? If one of the jokers is taken care of by the first sheet for half the decks, then the third sheet could supply the extra cards needed for a larger number of decks; if the decks are 54-card decks with two jokers, three cards repeated 21 times now is enough for 42 decks; if they're 55 decks, with two jokers and one extra card, the most common size, 63 cards can include five cards repeated twelve times - plus a full set of three extra cards, which would be superfluous only half the time, leading to one wasted card for every twenty-six decks.
And with the Tarot size cards? Well, two sheets would take care of 70 of the cards; eight cards and two extras could appear three times on a third sheet.
So one usually can manage fairly well, even if the size of the sheets is not a good match to the number of cards that is needed.