Of course, many different encryption principles have been seen in the devices covered in this chapter. One could imagine combining many of these techniques in a single elaborate device, such as the following:

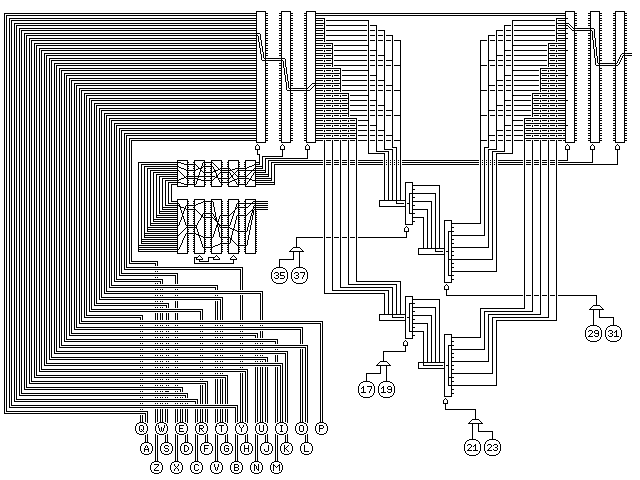
The heart of this device is two pairs of two half rotors, each pair with one with five inputs and ten outputs and one with five inputs and fifteen outputs, as in the improved French version of the B-211.
The coordinates for each letter of the alphabet are varied by preceding and following that part of the device by three conventional rotors. Almost conventional, that is, since these rotors all have two duplicate concentric sets of wiring, so that each letter is connected to its home in both row and column. Note that since these rotors have 26 positions, one letter bypasses the part of the device that is like the B-21.
And to top it all off, these six rotors are advanced by means of a SIGABA-like setup. Obviously too bulky and expensive to build out of real electromagnetic components, and yet fascinating.
Here is an example of an interesting rotor machine design using some of the ideas suggested by the design of the Uhr Box:
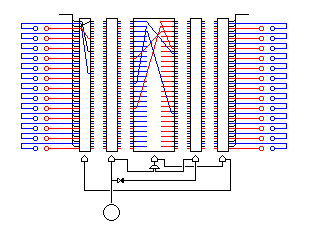
The arrangement for rotor motion is of interest. With each letter enciphered, a pinwheel is used to select whether rotor 2 or rotor 4 moves. Rotor 3 moves whenever a notch on either of those rotors is advanced, and then it advances rotor 5, which advances rotor 1, normally. Given multinotched rotors, this produces a fairly irregular movement with only one pinwheel.
However, the main unusual feature of the design is the way the rotors are wired.
As may not be readily apparent from the diagram, unless you are familiar with the conventions I've used in previous diagrams in this chapter, the rotors have two concentric rings of 26 contacts on each side.
Rotors 1, 2, 4, and 5 are wired like this:
The middle rotor connects the 26 contacts in the outer ring on one side to the 13 odd contacts of the inner rings on both sides, and the 26 contacts in the outer ring on the other side to the 13 even contacts of the inner rings on both sides.
Plaintext enters through the contacts on the outer ring on the left side of the rotor stack, and ciphertext leaves through the contacts on the outer ring on the right side.
On each side of the rotor stack, a plugboard controls the reflection of the odd contacts of the inner ring to the even contacts of the inner ring.
When a letter is enciphered, its signal first passes through the outer rings of rotors 1 and 2 in a normal rotor machine fashion.
Then, rotor 3 sends the signal through the inner rings, either of rotors 2 and 1 or of rotors 4 and 5, through their odd (or even) contacts, to be reflected back through the even (or odd) contacts of rotors 1 and 2 or rotors 5 and 4.
And then rotor 3 takes the reflected signal, and sends it through the outer rings of rotors 4 and 5 to continue in a normal rotor machine fashion.
There is some potential for additional flexibility in the design; for example, it would still work if the two plugboards were cross-wired (but not if they were merged into one), and the specially-wired rotor used as rotor 3 does not absolutely have to be in the central position.
In the section on the Enigma, I noted that if one shorted the indicator lights with diodes, it would be possible to attach the rotors to the lamps instead of the keys. This would allow one to design an Enigma in which the rotors could be switched from being connected to the keys or the lamps, so that a plugboard could be placed between the keys and the lamps. In this way, enciphering and deciphering would both be possible, but a letter could represent itself.
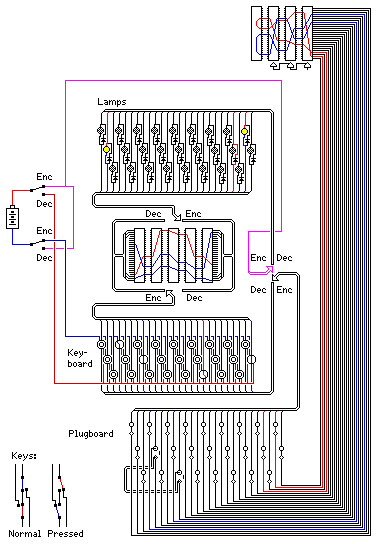
This diagram illustrates how this principle could be taken to its ultimate conclusion. On the left hand side of the keyboard and lampboard, a letter is being shown as being enciphered, and on the right hand side a letter is shown as being deciphered. Note how the polarity needs to be taken into account in enciphering mode, so that the diodes across the lamps do not prevent normal Enigma-like operation.
Here are a couple of other attempts to construct elaborate rotor machines combining principles we've seen in previous examples. The first also uses rotors with two concentric rings of 26 contacts, but this time the two sets of contacts are wired differently, not in parallel.
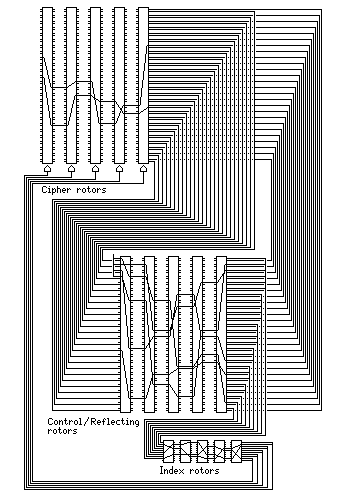
The cipher rotors act a bit like those in the Enigma; the plaintext letter causes electricity to go from left to right, and then the signal returns, going right to left, to produce the ciphertext letter. However, the returning signal uses the second set of contacts, and so the cipher is not reciprocal.
The general structure of the machine is like the SIGABA; but the extra set of contacts in the control rotors is used to provide an ever-changing "reflecting rotor" for the cipher rotors.
The following (originally done for use as a background, with different colors) illustrates a double-sized SIGABA. However, five of the signals controlling the ten cipher rotors are created somewhat differently, using a method from a rotor-based telecipher machine, the M-228, which we will encounter later.
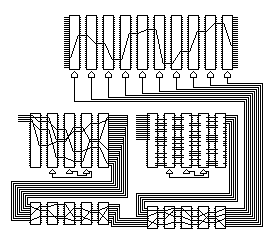
The five new control signals have some poor properties, but they nicely complement the SIGABA-type ones, since they have an exact 50% probability of being active.
Changing the wiring a bit (and making more rotors electrically controlled) gives us this:
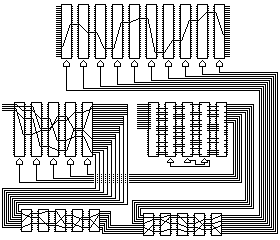
and the behavior of the rotor machine this schematic attempts to describe is the following:
The rotor banks in the illustration can be designated as follows:
Cipher (10 rotors) Control 1 Control 2 Index 1 Index 2
and operate as follows:
The Control 2 rotors have 13 live inputs, and are a bank of five rotors. The middle rotor (rotor 3) is the fast rotor, rotor 4 is medium, and rotor 2 is slow. Rotors 1 and 5 in the Control 2 bank are shown here as stators, rotors whose position is only changed when the initial setting of the machine is applied, like the rotors in the index banks. (Basically, this portion of the diagram was simply taken from the illustration of the M-228; I could have shown all five rotors moving, and had them multinotched to make that reasonable, but that would not be important for illustrating the principle.)
Ten outputs from the Control 2 rotors are used. Five are used to control the stepping of the Control 1 rotors.
The Control 1 rotors have five live inputs. Their outputs are tied together in groups of 5, 5, 4, 3, 3, 2, 1, 1, and 1 to create ten outputs. (Again, this part is simply directly taken from a SIGABA illustration.)
These ten outputs are fed into the Index 1 stators, which are a bank of five 10-contact rotors. The outputs are then tied together in five groups of two. These five inputs, together with the five other outputs from the Control 2 rotors, form the ten inputs into the Index 2 stators.
The ten outputs from the Index 2 stators are then used to control the stepping of the ten cipher rotors.
While the design above has the drawback that the SIGABA-style superior control rotors may occasionally remain immobile, because only the M-228 style ones have unused output contacts, this design causes five of the ten cipher rotors to be controlled by a set of control rotors (the SIGABA-style ones) that are themselves controlled by control rotors (the M-228 style ones) also used to directly control the other five cipher rotors. Not explicit in the diagram is a timing issue requiring a more basic redesign; in the original SIGABA, the cipher rotors move in response to the control rotor position at one time, and the control rotors advance at another time, requiring two clock phases; as the SIGABA-style control rotors can't move simultaneously with either the M-228 style control rotors or with the cipher rotors, we now need three clock phases.
The M-228 style rotors produce 10 outputs with, individually, an exact 50% probability of being active. But not only is it possible for the five outputs used for stepping the SIGABA-style control rotors to all be inactive, the drawback noted above, it is also possible for the five outputs which are routed to the cipher rotors to be inactive as well. Since the SIGABA-style control rotors must produce an active output, however, it will still be the case that some of the cipher rotors will move from one letter to the next. But this can be avoided, if one is willing to give up an exact 50% probability of activity for the output signals from the M-228 style control rotors. Since we need ten outputs, we cannot perform exactly the same modification that Frank Rowlett made to the SIGCUM; instead, we can use eight active inputs to the M-228 style control rotors, and tie their outputs together in pairs. This results in outputs that have about a 52.03% probability of being active.
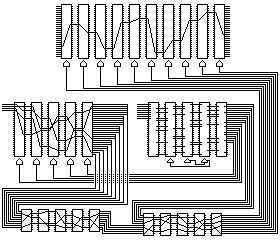
In practice, of course, I would advocate having all five of the M-228 style control rotors move, ensuring that even the slow rotor of five move by making them multinotched.
Incidentally, advancing five cipher rotors using the output of a M-228 style control rotor bank is easy to understand as making sense; there are 32 possible alphabets for each letter, and so the cipher is strongest when any one of them might be chosen with equal possibility.
However, a rotor machine has the ability to produce many more than 32 alphabets. So, it is clear that using the same alphabet twice in a row is something desirable to be avoided. But that isn't the only reason for the very unequal size of the groups of outputs of the SIGABA-style control rotors that are tied together. A rotor that is advanced exactly half the time will, on average, move at one-half the speed of a fast rotor.
By advancing the cipher rotors at unequal speeds, it is possible to proceed more quickly through the space of possible alphabets they can produce, since different positions on different cipher rotors will be more quickly brought together. Different index rotor settings on the SIGABA changed the extent of this disparity, as they could bring together large bunches with large, and small with small, or they could bring together a large bunch and a small bunch. So different SIGABA encipherments could involve fundamentally different paths through the alphabet space provided by the cipher rotors.
A simpler construct, based on the SIGABA, is illustrated below:
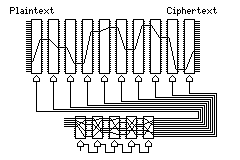
which is simply how I, and perhaps others, imagined the SIGABA might have worked after reading a brief description of it by David Kahn from about 1980, and seeing the first pictures of it that were released some years later. Since the actual design didn't involve the five ten-contact rotors moving, this design would have been even more expensive to build.
Of course, a more elaborate version of the SIGABA is more likely to be created as a computer simulation than with a physical embodiment. And some features, such as the index rotors, don't really make sense on a computer, since the internal wirings of the machine could be scrambled directly with ease. The rotor wirings can be key-dependent as well. And, of course, the rotors can be replaced by S-boxes, with addition operations between them, since the two ends of the rotor can rotate separately.
An example of an elaborate SIGABA-based rotor construct that doesn't go quite as far as to stop involving rotors, but which does have some modifications in the direction of being appropriate for a computer, might be the following:
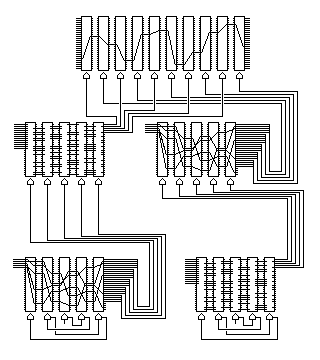
Here, we have ten cipher rotors, and they are alternately controlled by one of two groups of control rotors, whose motions are themselves controlled by super-control rotors.
Note that in the two groups of control and super-control rotors, one group has the super-control rotors having the plain design without precautions taken to prevent an all-zeroes group of control signals being output, and the other group has the control rotors having this design. Thus, the ten cipher rotors are divided into two alternating categories, receiving control signals with different properties. Both groups have weaknesses, but these weaknesses cancel out; one set of five signals always includes at least one active signal, but may not change from the encipherment of one character to the next, while the other set of five signals may consist of all zeroes, but is sure to be changed with the next character.
Incidentally, this design is also useful as an illustrative example of how to deal with a problem that affects the use of rotor machines.
The starting position of the rotors for the encipherment of a message is somewhat analogous to the initialization vector used with many block cipher modes. However, the analogy is not perfect, and so it is often considered advantageous to encrypt this starting position before sending it out as the message indicator.
If one does so with the encryption tool one happens to have to hand, that is, the rotor machine itself, however, a problem develops. Doing so with the rotor machine set at a fixed ground setting results in the rotor position being enciphered by a fixed series of simple substitutions. The story of the cryptanalysis of the ENIGMA illustrates how this threat was dealt with through such measures as bigram tables.
The actual SIGABA dealt with that by sending the starting positions of the control rotors, and then having the setting up of that position take a number of steps which led to movement of the cipher rotors, so that their starting position was derived from the message indicator in a more complex fashion.
The use of the SIGABA in the POTUS-PRIME link addressed the issue in a more direct fashion, with a code table of rotor starting positions, each entry of which was only used once.
For the elaborate construct shown above, one way to allow the full power of the device to be brought to bear on the starting positions of its thirty rotors, for a very large volume of messages, might be to use a table, replaced each day, like the following:
order 1 2 3 4 5 6 A 356142 QPZAL AMYUP LVANQ YGIPZ UQRPT OLYIR B 261435 AHPIE NZLTO VWOXZ TRLGV KXIQN WENXO C 634215 MXOIZ EXNZO WNZCO COVFS VIXPC XECPW ... Z 425136 TPCEI RMLSU XQPSN ISENR XOEWM EJMSU
by means of which a sequence of seven letters would indicate the ground setting as follows: the first letter would indicate the order in which the six columns of settings were used, and the following six letters would indicate the positions, for sending the message indicator, of the machine's thirty rotors, five at a time. Thus, with the first seven letters being AAXYUVW, the first five rotors, perhaps the leftmost five cipher rotors, would be set initially to the position LVANQ, since column 3 is to be used first, and with the first seven letters being BAXYUVW, the first five rotors would be set to AMYUP, since column 2 is to be used first.
Then, that ground setting would be used to encipher thirty letters giving the actual rotor starting position for the message itself. If the volume of messages is low enough that the first seven letters are unlikely to be duplicated, it is clear this should be adequate.
For a larger message volume, the number of messages with the first seven letters the same that would be safe is the same as the volume of messages that could be sent using a plain fixed ground setting. This is clear because the first seven letters are an encrypted rotor position, and that position is used directly to encipher the thirty letters of the actual initial rotor position. This means that this scheme hasn't really solved the problem of a rotor machine not being suited to encipher starting rotor positions, it has only postponed it.
Because the device used above as an example is based on the SIGABA, to obtain a sound scheme of enciphering initial rotor settings, it would make sense to look at the scheme actually used with the SIGABA for inspiration. After enciphering each group of five letters of the rotor position to use, one could set the five rotors of the cipher machine to which they apply to that position. In this way, even within a single ground setting, the relationship between the thirty letters sent and the starting rotor position used would become more complicated than a series of thirty monalphabetic substitutions.
Using bigram tables like those of the Enigma would, of course, be a way to produce a considerably more complicated relationship between the message indicator and the initial rotor settings, and there are many different ways in which bigram tables could be employed. But could the ground setting table above be used more than once as a means of complicating this relationship as well? And if so, how: by setting up all thirty rotors several times, or by constructing the table so that no letter is duplicated in any of the thirty columns of letters, and using it to encipher individual letters? Or is there a more satisfactory way of doing this?
Next
Chapter Start
Skip to Next Chapter
Table of Contents
Main Page