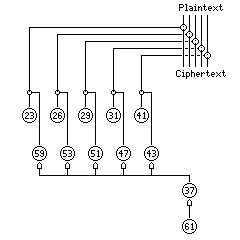
The Lorenz SZ-40 and SZ-42 cipher machines were widely used by German forces during World War II. It was primarily to break this machine's cipher that the British devised what is now considered the world's first electronic computing machine, the once-secret COLOSSUS.
It had twelve pinwheels, all of which could have all their pins set by the user. Ten of these pinwheels formed two groups of five, and one wheel from each group inverted its corresponding plaintext bit when a pin was active on it.
The wheels of the first group had sizes 41, 31, 29, 26, and 23. Those of the second group had sizes 43, 47, 51, 53, and 59.
Two additional wheels were of size 37 and 61. The wheels of the first group, and the wheel with 61 positions, advanced one position with every letter enciphered. When the current pin on the 61-position wheel was active, the wheel with 37 positions advanced one space. When the current pin on the 37-position wheel was active, then the wheels of the second group advanced one space.
The following diagram illustrates the workings of the Lorenz Schlusselzusatz:

Although the SZ-40 appears to be a simple design, and a very similar design proposed by Col. Parker Hitt, but without the feature that the stepping of five wheels was irregular, was shown to be insecure, the British found breaking SZ-40 messages to be a more difficult problem than breaking Enigma messages. Some cribs were available that helped them to break into the system; part of the difficulty seems to have come from the limited availability of resources, and another part from the lack of captured equipment and tables: for example, the list giving numbers representing wheel settings was never captured, while the bigram tables for the Enigma were.
The machines used in cracking messages on the Lorenz Schlusselzusatz, known as HEATH ROBINSON and COLOSSUS, have been described to a limited extent in the open literature. A paper by F. L. Carter, in "Cryptography and Coding", the proceedings of the 6th IMA International Conference, from December, 1997, gave significant additional details of how COLOSSUS was used.
HEATH ROBINSON, named after a British cartoonist who, like Rube Goldberg in the U.S., was famous for his drawings of elaborate contraptions (although the styles of the two artists were very different), worked by comparing the holes punched in two paper tapes, one containing an intercepted message, and one containing a reproduction of part of the sequence of bits the pinwheels of an SZ-40 might be expected to generate. The tapes were padded with nulls to make them of relatively-prime length, and HEATH ROBINSON indicated at what point in the motions of both tapes a correlation between the two was found. This required the two tapes to move synchronously, and so the sprocket holes had to be used, which limited the speed at which the tapes could move.
COLOSSUS was built to improve on HEATH ROBINSON by generating the SZ-40 stream cipher output, or the portion thereof used for testing (such as the output of the five always-moving wheels) electronically. This way, the tapes could be moved on pulleys, at very high speeds, without any problems. A glass mask with lens-shaped patterns was used so that the light shining through the round holes on the paper tape would produce an approximation to a square wave. Thus, the paper tape, in addition to supplying input data, actually supplied the clock signal for COLOSSUS' internal logic. Apparently, in generating the pattern which a second paper tape provided on HEATH ROBINSON, COLOSSUS was capable of some sort of conditional branching, on which its claim (having been first installed in December 1943) to being the first electronic computer rests.
The paper by Carter sheds considerable light on the cryptanalytic principles behind COLOSSUS. The 5-level code used for teletypewriters was designed to minimize mechanical wear and tear; hence, the codes for the most frequent letters E and T, as well as the code for the space, consisted of a single 1 bit and four zeroes. This meant that zeroes predominated in the plaintext, and in addition, it meant that for any two characters in succession, corresponding bits in them were more likely than not to be the same. (Of course, this characteristic of the plaintext was weaker than the higher frequency of zeroes, and was a consequence of the higher frequency of zeroes.)
Since one set of pinwheels in the SZ-40 did not advance with every character enciphered, this meant that when two succeeding cipher characters had a corresponding bit that changed, then it was likelier than not that the fast pinwheel for that bit was at a point where two adjacent pins were in different positions, and when two succeeding cipher characters had a corresponding bit that stayed the same, then the probability that the fast pinwheel had two similar pins was also increased. (Since the slow pinwheels did move half the time, this correlation was again weakened, but it still existed.)
Since COLOSSUS and HEATH ROBINSON both used sample keystreams from the fast pinwheels, one might then think, once one has been informed of the basic principle behind their attack, that one could use paper-and-pencil methods to break the Schlusselzusatz. After all, the period of each of the wheels in the first group is known. Take each of the five bits in a character separately, and then compare them in succeeding periods of the corresponding wheel in the first group. Where two bits are repeatedly the same or different, one has an inactive position of the control wheel.
The problem with that, and (in my opinion, the primary) reason why one must instead use multiple bits from a character, is that one does not have a steadily moving control wheel; the control wheel, with 37 positions, is itself controlled by a wheel with 61 positions. Thus, there is no simple, regular control sequence that can be established by lining up successive values of a single bit at fixed intervals.
In the papers on the Colossus, that the pin settings for the fast pinwheel were chosen so that like and unlike pairs of pins were as close to being equally likely as possible, was given as the reason that it was not possible in practice to correlate a single pinwheel at a time, but correlations involving pairs of pinwheels were easier. An abbreviated notation was used to specify types of tests to be run with COLOSSUS: one test was a simple correlation on two particularly favored pinwheels; other tests searched for common pairs of characters, such as space-figures shift, or figures shift-period. In some messages, doubled letters were quite common, and there was a test that looked for them as well.
There is also a paper by W. T. Tutte, one of the cryptanalysts who worked on messages enciphered by the Schlusselzusatz at Bletchley Park, now available on the site of Frode Weierud that details the early days of the cryptanalysis of the Schlusselzusatz, codenamed Tunny by the British. That source notes the following:
Originally, the machine was used with a 12-letter indicator, which contained initial positions for all twelve pinwheels without encryption (e.g. under a "ground setting"). Each letter stood for an initial position, and the wheels had only 25 positions which a letter could indicate, except, of course, for the wheel with only 23 positions.
The initial analysis which allowed the British to determine the basic principles of the Sclusselzusatz was aided by the reciept of some pairs of messages enciphered with the same starting positions, including one re-encipherment of a long message with changes in word spacing and punctuation with exactly the same indicator.
In 1943, the Germans switched to using a number as an indicator, which was assumed to signify a 12-letter combination from a list. Later, they switched from changing pinwheel settings once a month to changing them each day, and they also modified the machine so that the wheels in the second group, instead of having their irregular motion controlled only by the 37 and 61 pinwheels, had that motion depend on a function of the pinwheels that moved with each character, or on the previous plain text (thus employing the autokey principle). However, the five wheels that stepped with every character continued to do so, and although the five slow wheels were controlled differently, they still either all moved or all stayed still, so the existing cryptanalytic approaches remained valid.
The General Report on Tunny, recently declassified by the British Government, gives some details of these modifications; four forms were known, and they were referred to as the "limitation" feature. The possibilities were:
Either just the previous pin on the 31-position wheel or the XOR of the previous pin on the 31-position wheel and on the 43-position wheel, and either of these two possibilities further XORed with the fifth bit of the plaintext character to characters prior to the current plaintext character.
The 43-position wheel is one of the wheels whose stepping is variable; "the previous position" refers, I believe, to the pin one place over on the wheel in the correct direction, and not necessarily to the pin used in the encipherment of the preceding character if the wheels whose stepping is variable did not move prior to the encipherment of the current character, as the other case would require an elaborate addition to remember past pin values.
With is feature in place, the five slow wheels moved if the current pin on the 37 pinwheel indicated motion, or if the limitation bit was zero, so the slow wheels only stayed put one-quarter of the time instead of one-half of the time, thus at least quantitatively reducing the basic weakness of the design.
Here is an illustration, using the symbolism I have employed in other diagrams on these pages, of the machine with these features added:
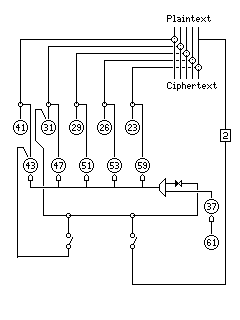
A delay of 2 is shown on the plaintext input, although in reality the paper tape input would just be read two positions earlier, as that would have been more awkwards to draw.
Also noted is that HEATH ROBINSON, and an improved version of it made later in the war, still continued to be used for one task which COLOSSUS could not perform, searching for key overlaps between messages, since COLOSSUS could only compare short sequences, such as those of the regularly-moving pinwheels, to the long message on the one tape it used.
Given that the pinwheel settings changed each day, if both COLOSSUS and HEATH ROBINSON were dependent on knowing the settings on the fast pinwheels, then it might seem that breaking Schlusselzusatz messages could not get off the ground. What was described above was only the simplest part of the process of attacking this traffic.
Knowing the periods of the fast pinwheels, one could attempt to find out their settings directly by lining up the bits of messages in relation to the fast pinwheel periods. The plaintext is mostly zeroes, and the slow pinwheels sometimes stop, and so, slightly more often than not, the bits will stay the same in the ciphertext when they stay the same on the fast pinwheel, and change where they change on the fast pinwheel.
In practice, rather than reconstructing the fast pinwheels at this step, perhaps because there was too much chance of errors inverting whole parts of the pinwheel, the results from the five bits of the character were combined to determine when the slow pinwheels did not move.
Once this could be done with confidence, then the step known as "rectangling" could be performed. If, for each bit of the message, one knew exactly which two pins on the two pinwheels contributed to the ciphertext, one could then combine information from successive parts of a long message to find out the pin settings on both pinwheels. (Of course, there would be no way to tell if one had inverted every pin on each wheel.) I have to admit that it seems to me that one would have to have already attempted to do a fair amount of reconstruction on the pinwheel settings before obtaining the necessary confidence in the pattern of slow wheel motion to be able to perform this step, but then the accounts of rectangling do admit themselves to be somewhat simplified.
If one had pinwheels of periods 7 and 5, then the pattern followed in placing bits, as long as the slow pinwheels continued to move without interruption, would look like this:
1 16 31 11 26 6 21 22 2 17 32 12 27 7 8 23 3 18 33 13 28 29 9 24 4 19 34 14 15 30 10 25 5 20 35
but because the slow pinwheels do stop, there would be jumps where instead of moving downwards and to the right, the message just moved downwards (the larger pinwheels which stop being shown here as written across).
The machine by Colonel Parker Hitt was noted briefly in the introductory page of this section. A recent book on Colossus, the electronic machine used in breaking the Schlusselzusatz cipher, contains a section with a suggestion that an equivalent machine, termed a "motorless" Schlusselzusatz, might have remained unbroken. (In fairness to the illustrious individuals advancing this notion, the section appears simply to be a transcript of part of a discussion, where those involved would not have had the time to mull things over properly.)
Since one would not have the situation where one set of five wheels remained still, it is true that the specific weakness used against the Schlusselzusatz would have been absent. However, given the fact of a plaintext in which zero bits were prominent, if one organized the appropriate bits of a message in as many columns as there were pins on one of the wheels used, then the bits along the columns would correlate with each other at regular intervals.
And these intervals would remain the same from one message to the next, regardless of the initial pinwheel positions, so the sizes of all the wheels could be established with confidence. Once the sizes of the wheels are known, using a single bit from a single message at a time, one can proceed directly to the process known as "rectangling", determining, from which pin on each of the two wheels contributes to enciphering a given bit of the message, the pinwheel settings.
If one couldn't improve on the Schlusselzusatz in the obvious way, by making the controlled wheels step either once or twice instead of either once or not at all, and options requiring a large amount of additional equipment, such as controlling each of the five controlled wheels independently was not possible, what else could be done?
One possibility might be to take an alternate output from the 61 wheel, the motor wheel that always steps, and XOR it with all five of the keystream output bits of the device. Now, when the controlled wheels all stayed still, the bits from the wheels that moved constantly would still, half the time, be XORed with different bits from one character to the next.
However, as this still happens to all five bits at the same time, and the irregular nature of the signal regulating the motion of half the wheels has already made it necessary to look at two bits at once, the result would simply be that the revealing windows into the sequences of the steadily-moving pinwheels would come half as often, as was the case with the "limitation" feature discussed above.
If we cannot eliminate having half the wheels of the Schlusselzusatz stop at irregular intervals, however, perhaps its other weakness, the absolutely regular movement of the other set of wheels could have been eliminated.
Take the output of the 37 wheel; use that output, OR an alternate output of the 61 wheel, to control the movement of the existing controlled wheels, and take that same output, OR the inverse of the same alternate output of the 61 wheel, to control the movement of the other set of wheels.
Now, when one set of wheels stands still, the position of the other set of wheels is no longer fixed in relation to its past and future positions, and so the method used by Colossus really is rendered ineffective.
The following diagram:
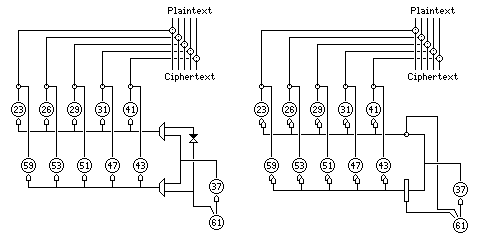
shows this design, and an alternate one with the additional modification of stepping the wheels either once or twice, since, in fact, there is no good reason, except possibly to avoid having to halve the speed of operation, not to do this. And once that is done, instead of requiring that one set of wheels steps each time by using two related signals, instead of having double stepping happen three-quarters of the time, it could happen half the time, or one-quarter of the time, and each set of wheels could double-step independently. So, instead of an OR with a single alternative output of the 61-wheel, one could use two alternative outputs, and in one case use an AND, and in the other an XOR, as shown in the second half of the diagram.
It might well be that at least the first example machine could have still been broken by the technology of World War II, and by heroic efforts such as were applied against the real Schulsselzusatz; the fact that I can't think of how they might have done it through a trivial extrapolation of the methods used in history as it was certainly doesn't eliminate the possibility that the geniuses who were working on the problem at the time could have found a way.
Next
Chapter Start
Skip to Next Section
Table of Contents
Main Page