I learned about the design of this machine from a page on the Crypto Museum web site. (Note: to remain consistent with the rest of the site, I use different terminology than that page. What they call a "drum", I call a "cage"; what they call a "contact cylinder", I call a "drum".)
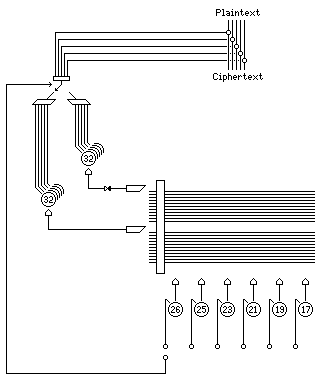
It is an ingenious and intricate device; its design cannot be fully expressed in the schematic notation I have been using in my diagrams of cipher machines, but I can still approximate it enough that I hope my diagram will be useful:

The basic design is similar to that of a normal Hagelin lug and pin machine. (The sizes of the six keywheels are speculation on my part; from photographs, the keywheels appear to be the same size as those of the regular lug and pin machines.)
Due to practical considerations, the cage containing the sliding bars with the lugs could only rotate once for every two characters enciphered. So the cage was divided into two halves, each with twelve bars. (The keywheels, each one relatively prime in size to the others, advance one position with each full rotation of the cage. Refer to the previous page on Hagelin lug and pin machines to review how this cipher mechanism operated.)
As in a normal Hagelin machine, each bar was pushed back in, and then slid out if one of its lugs encountered an active pin on the corresponding keywheel, once per each full revolution of the cage.
To deal with the limitation of only being able to use twelve lug bars per character, the two sets of lug bars were used twice; first, each lug that had been pushed by active pins advanced a drum with 32 positions one space, and then, for the next character, the lugs that had not been pushed by active pins advanced a second drum with 32 positions one space each.
These two drums always contained all 32 different combinations of mark and space, but in a jumbled order; the photo on the Crypto Museum web site will show the pluggable segments that go into the drums.
Each of the six keywheels is also sensed at an alternate position. As part of the keying procedure, one of those outputs is chosen for switching between the two drums as the source for the 5-bit symbol to be XORed with the plaintext. Incidentally, in the Hagelin documentation, it is noted that Mark (+) is treated as 0 and Space (-) is treated as 1, for this purpose.
The fact that the drums can only advance from 0 to 12 positions for each character enciphered suggests that points of attack should exist for this machine's cipher.
The switching between the outputs of the two drums is controlled by the pins on only one keywheel, so it is regular. If one has known plaintext, all six possibilities of the choice of the pinwheel used as the source will have to be tried, but once one has the right one of those possibilities, one can proceed as follows:
Line up the presumed keystream in rows of that pinwheel's period (26, 25, 23, 21, 19, or 17). There will usually be pairs of adjacent columns where the front drum, the one which uses each group of 12 bars first without inversion (let us call this case A), is used twice in a row, and where the rear drum, the one which uses each group of 12 bars second with inversion (let us call this case B), is used twice in a row.
Then, in the first column of each pair, each five-bit keystream value will only be followed in the second column either by itself, or by the twelve other values in the following twelve positions on the drum.
Assuming sufficient known plaintexts with the same key, one can then reconstruct the two drums.
What about the fact that after the front drum is advanced by from 0 to 12 positions, for the next character enciphered, the rear drum is advanced by twelve minus that number of positions? Can that be used?
At first, it might seem that this is not the case. After all, if the choice between front and rear drums is AABB, for example, the advance between B and B is two characters later than the one between A and A; one can't have AxB where x is both A and B.
But in the sequence ABAB, the AxA part is followed, one character time later, by the BxB part. And the front drum is advanced from 0 to 24 positions between the two "A"s, and then by twenty-four minus that number of positions between the two "B"s.
So in this case, we now have an exact correlation between the two drum positions, so that if the reconstruction of the drums by the previous step is vague and incomplete in some areas, it can be corrected and reinforced.
Can this attack be avoided by setting the pins on the keywheel used for switching between the two drums with a sequence like 001110001100... so that there are no stretches of 0101 or 1010?
No; in a case like ABBAAB where AxxxA is followed, one character time later, by BxxxB, it is true that now the drum may make an unknown number of complete revolutions. However, twelve times four, or twelve times any other number, is a constant, and so its residue modulo 32 is also a constant; so the difference between the two drum positions in this case still has only one possibility, not several possibilities depending on how many full revolutions occurred.
And if the AA and BB cases can be detected by the fact that five-bit sequences in the first column can only be followed by a limited number of possibilities in the following column, everything else between them must be made up of "A"s and "B"s in alternation.
So, although in practice one will have a limited amount of known plaintext, and there will be much work and many false leads, it will be relatively easy to reconstruct the bits on the two drums, and the pin settings on the keywheel used for switching between them.
At this point, then, one can determine (with many gaps, because of the duplicates that gave an entry into the cipher) the sequence of numbers of active bars that the cage has produced. Then one can attack the lug settings and the pin settings on the other keywheels following the same procedures as used for a regular Hagelin lug and pin machine.