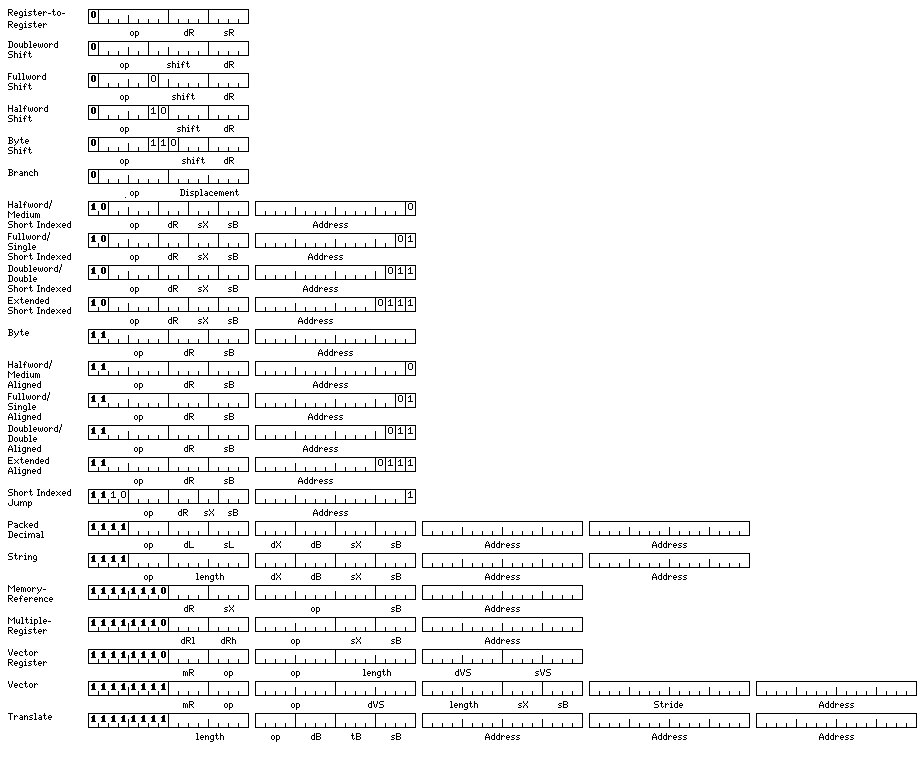
A very complex imaginary architecture was defined here, primarily motivated by what I perceived as a flaw in the architecture of the IBM System/360: that the displacement field in an instruction was only 12 bits long, instead of 16 bits long, as on many microprocessors or the PDP-11.
On the previous page, the possibility of creating instruction formats very closely resembling that of the IBM System/360 which would address this issue was examined.
On this page, an alternative approach, resulting in something closer to my imaginary architecture, able to retain most of its capabilities, is illustrated. Important similarities to the 360 are retained: registers are in sets of 16 rather than 8, and the instructions are limited to a small number of lengths, with length decoding kept very simple.
Here are the instruction formats:

Because sets of 16 registers are used, a full indexed memory-reference instruction is forced to be 48 bits long. So a non-indexed format is provided, and also a short indexed format. In the short indexed format, the destination register is one of general registers 0 to 7, the index register is one of general registers 1 through 7, and the base register is one of base registers 8 to 15; as in my architecture, unlike the System/360, a separate set of registers is used for base registers rather than having general registers be consumed by being allocated as base registers, even though there are sixteen of each instead of eight.
It's all very well to draw pretty pictures, but is there actually enough opcode space to fit all the instructions in that I would want using these formats?
There's only one way to find out: allocate them.
The fixed-point register-to-register instructions take up half of the opcode space allocated to 16-bit instructions:
00 SWBR Swap Byte Register 01 CBR Compare Byte Register 02 LBR Load Byte Register 04 ABR Add Byte Register 05 SBR Subtract Byte Register 08 IBR Insert Byte Register 09 UCBR Unsigned Compare Byte Register 0A ULBR Unsigned Load Byte Register 0B XBR XOR Byte Register 0C NBR AND Byte Register 0D OBR OR Byte Register 10 SWHR Swap Halfword Register 11 CHR Compare Halfword Register 12 LHR Load Halfword Register 14 AHR Add Halfword Register 15 SHR Subtract Halfword Register 16 MHR Multiply Halfword Register 17 DHR Divide Halfword Register 18 IHR Insert Halfword Register 19 UCHR Unsigned Compare Halfword Register 1A ULHR Unsigned Load Halfword Register 1B XHR XOR Halfword Register 1C NHR AND Halfword Register 1D OHR OR Halfword Register 1E MYHR Multiply Extensibly Halfword Register 1F DYHR Divide Extensibly Halfword Register 20 SWR Swap Register 21 CR Compare Register 22 LR Load Register 24 AR Add Register 25 SR Subtract Register 26 MR Multiply Register 27 DR Divide Register 28 IR * Insert Register 29 UCR Unsigned Compare Register 2A ULR * Unsigned Load Register 2B XR XOR Register 2C NR AND Register 2D OR OR Register 2E MYR Multiply Extensibly Register 2F DYR Divide Extensibly Register 30 SWLR Swap Long Register 31 CLR Compare Long Register 32 LLR Load Long Register 34 ALR Add Long Register 35 SLR Subtract Long Register 36 MLR Multiply Long Register 37 DLR Divide Long Register 39 UCLR Unsigned Compare Long Register 3B XLR XOR Long Register 3C NLR AND Long Register 3D OLR OR Long Register 3E MYLR Multiply Extensibly Long Register 3F DYLR Divide Extensibly Long Register
The instructions marked with an asterisk are valid only in 64-bit mode. Load sign-extends into the unused high portion of the register, Unsigned Load clears it, Insert leaves it undisturbed. Multiply and Divide take two inputs and return one output of the same length, just like Add and Subtract. Multiply Extensibly returns a double-length product, with the additional part in the high portion of the destination register if possible; if not, the high part of the product is in the destination register, and the low part is in the following register. Divide Extensibly has a double-length dividend, a single-length divisor, a double-length quotient and a single-length remainder. The quotient is therefore placed where the dividend was found, and the remainder in the next available register.
Because IEEE 754 floating-point will be used, there will be no need for unnormalized floating-point instructions, and so but 1/4 of the opcode space for 16-bit instructions is used by the floating-point instructions:
40 SWMR Swap Medium Register 41 CMR Compare Medium Register 42 LMR Load Medium Register 44 AMR Add Medium Register 45 SMR Subtract Medium Register 46 MMR Multiply Medium Register 47 DMR Divide Medium Register 48 SWFR Swap Floating Register 49 CFR Compare Floating Register 4A LFR Load Floating Register 4C AFR Add Floating Register 4D SFR Subtract Floating Register 4E MFR Multiply Floating Register 4F DFR Divide Floating Register 50 SWDR Swap Double Register 51 CDR Compare Double Register 52 LDR Load Double Register 54 ADR Add Double Register 55 SDR Subtract Double Register 56 MDR Multiply Double Register 57 DDR Divide Double Register 58 SWER Swap Extended Register 59 CER Compare Extended Register 5A LER Load Extended Register 5C AER Add Extended Register 5D SER Subtract Extended Register 5E MER Multiply Extended Register 5F DER Divide Extended Register
Only half of what is left is needed for the shift instructions:
60 110 SHLB Shift Left Byte 60 10 SHLH Shift Left Halfword 60 0 SHL Shift Left 61 110 SHRB Shift Right Byte 61 10 SHRH Shift Right Halfword 61 0 SHR Shift Right 63 110 ASRB Arithmetic Shift Right Byte 63 10 ASRH Arithmetic Shift Right Halfword 63 0 ASR Arithmetic Shift Right 64 110 ROLB Rotate Left Byte 64 10 ROLH Rotate Left Halfword 64 0 ROL Rotate Left 65 110 RORB Rotate Right Byte 65 10 RORH Rotate Right Halfword 65 0 ROR Rotate Right 66 110 RLCB Rotate Left through Carry Byte 66 10 RLCH Rotate Left through Carry Halfword 66 0 RLC Rotate Left through Carry 67 110 RRCB Rotate Right through Carry Byte 67 10 RRCH Rotate Right through Carry Halfword 67 0 RRC Rotate Right through Carry 68 SHLL Shift Left Long 69 SHRL Shift Right Long 6B ASRL Arithmetic Shift Right Long 6C ROLL Rotate Left Long 6D RORL Rotate Right Long 6E RLCL Rotate Left through Carry Long 6F RRCL Rotate Right through Carry Long
leaving the other half for the relative branch instructions:
71 BL Branch if Low 72 BE Branch if Equal 73 BLE Branch if Low or Equal 74 BH Branch if High 75 BNE Branch if Not Equal 76 BHE Branch if High or Equal 77 BNV Branch if No Overflow 78 BV Branch if Overflow 7A BC Branch if Carry 7B BNC Branch if No Carry 7F BRA Branch
This should have been the hard part, as restricting the 32-bit memory-reference instructions to aligned operands, and making use of that to distinguish between operations on data of different lengths by means of the least-significant bits of the address field (an idea pioneered by the SEL 32 computer) produces an extreme saving of opcode space, but even with that saving, in order to have as much space available as I deemed required, it was necessary to complicate the formatting of the 48-bit and 64-bit long instructions:
80 0 SWHX Swap Halfword Indexed 80 01 SWX Swap Indexed 80 011 SWLX Swap Long Indexed 82 0 CHX Compare Halfword Indexed 82 01 CX Compare Indexed 82 011 CLX Compare Long Indexed 84 0 LHX Load Halfword Indexed 84 01 LX Load Indexed 84 011 LLX Load Long Indexed 86 0 STHX Store Halfword Indexed 86 01 STX Store Indexed 86 011 STLX Store Long Indexed 88 0 AHX Add Halfword Indexed 88 01 AX Add Indexed 88 011 ALX Add Long Indexed 8A 0 SHX Subtract Halfword Indexed 8A 01 SX Subtract Indexed 8A 011 SLX Subtract Long Indexed 8C 0 MHX Multiply Halfword Indexed 8C 01 MX Multiply Indexed 8C 011 MLX Multiply Long Indexed 8E 0 DHX Divide Halfword Indexed 8E 01 DX Divide Indexed 8E 011 DLX Divide Long Indexed 90 0 IHX Insert Halfword Indexed 90 01 * IX Insert Indexed 92 0 UCHX Unsigned Compare Halfword Indexed 92 01 UCX Unsigned Compare Indexed 92 011 UCLX Unsigned Compare Long Indexed 94 0 ULHX Unsigned Load Halfword Indexed 94 01 ULX Unsigned Load Indexed 94 011 ULLX Unsigned Load Long Indexed 96 0 XHX XOR Halfword Indexed 96 01 XX XOR Indexed 96 011 XLX XOR Long Indexed 98 0 NHX AND Halfword Indexed 98 01 NX AND Indexed 98 011 NLX AND Long Indexed 9A 0 OLX OR Halfword Indexed 9A 01 OX OR Indexed 9A 011 OLX OR Long Indexed 9C 0 MYHX Multiply Extensibly Halfword Indexed 9C 01 MYX Multiply Extensibly Indexed 9C 011 MYLX Multiply Extensibly Long Indexed 9E 0 DYHX Divide Extensibly Halfword Indexed 9E 01 DYX Divide Extensibly Indexed 9E 011 DYLX Divide Extensibly Long Indexed A0 0 SWMX Swap Medium Indexed A0 01 SWFX Swap Floating Indexed A0 011 SWDX Swap Double Indexed A0 0111 SWEX Swap Extended Indexed A2 0 CMX Compare Medium Indexed A2 01 CFX Compare Floating Indexed A2 011 CDX Compare Double Indexed A2 0111 CEX Compare Extended Indexed A4 0 LMX Load Medium Indexed A4 01 LFX Load Floating Indexed A4 011 LDX Load Double Indexed A4 0111 LEX Load Extended Indexed A6 0 STMX Store Medium Indexed A6 01 STFX Store Floating Indexed A6 011 STDX Store Double Indexed A6 0111 STEX Store Extended Indexed A8 0 AMX Add Medium Indexed A8 01 AFX Add Floating Indexed A8 011 ADX Add Double Indexed A8 0111 AEX Add Extended Indexed AA 0 SMX Subtract Medium Indexed AA 01 SFX Subtract Floating Indexed AA 011 SDX Subtract Double Indexed AA 0111 SEX Subtract Extended Indexed AC 0 MMX Multiply Medium Indexed AC 01 MFX Multiply Floating Indexed AC 011 MDX Multiply Double Indexed AC 0111 MEX Multiply Extended Indexed AE 0 DMX Divide Medium Indexed AE 01 DFX Divide Floating Indexed AE 011 DDX Divide Double Indexed AE 0111 DEX Divide Extended Indexed C0 0 SWHA Swap Halfword Aligned C0 01 SWA Swap Aligned C0 011 SWLA Swap Long Aligned C2 0 CHA Compare Halfword Aligned C2 01 CA Compare Aligned C2 011 CLA Compare Long Aligned C4 0 LHA Load Halfword Aligned C4 01 LA Load Aligned C4 011 LLA Load Long Aligned C6 0 STHA Store Halfword Aligned C6 01 STA Store Aligned C6 011 STLA Store Long Aligned C8 0 AHA Add Halfword Aligned C8 01 AA Add Aligned C8 011 ALA Add Long Aligned CA 0 SHA Subtract Halfword Aligned CA 01 SA Subtract Aligned CA 011 SLA Subtract Long Aligned CC 0 MHA Multiply Halfword Aligned CC 01 MA Multiply Aligned CC 011 MLA Multiply Long Aligned CE 0 DHA Divide Halfword Aligned CE 01 DA Divide Aligned CE 011 DLA Divide Long Aligned DO 0 IHA Insert Halfword Aligned DO 01 * IA Insert Aligned D2 0 UCHA Unsigned Compare Halfword Aligned D2 01 UCA Unsigned Compare Aligned D2 011 UCLA Unsigned Compare Long Aligned D4 0 ULHA Unsigned Load Halfword Aligned D4 01 ULA Unsigned Load Aligned D4 011 ULLA Unsigned Load Long Aligned D6 0 XHA XOR Halfword Aligned D6 01 XA XOR Aligned D6 011 XLA XOR Long Aligned D8 0 NHA AND Halfword Aligned D8 01 NA AND Aligned D8 011 NLA AND Long Aligned DA 0 OLA OR Halfword Aligned DA 01 OA OR Aligned DA 011 OLA OR Long Aligned DC 0 MEHA Multiply Extensibly Halfword Aligned DC 01 MEXA Multiply Extensibly Aligned DC 011 MELA Multiply Extensibly Long Aligned DF 0 DYHA Divide Extensibly Halfword Aligned DF 01 DYA Divide Extensibly Aligned DF 011 DYLA Divide Extensibly Long Aligned E0 0 SWMA Swap Medium Aligned E0 01 SWFA Swap Floating Aligned E0 011 SWDA Swap Double Aligned E0 0111 SWEA Swap Extended Aligned E2 0 CMA Compare Medium Aligned E2 01 CFA Compare Floating Aligned E2 011 CDA Compare Double Aligned E2 0111 CEA Compare Extended Aligned E4 0 LMA Load Medium Aligned E4 01 LFA Load Floating Aligned E4 011 LDA Load Double Aligned E4 0111 LEA Load Extended Aligned E6 0 STMA Store Medium Aligned E6 01 STFA Store Floating Aligned E6 011 STDA Store Double Aligned E6 0111 STEA Store Extended Aligned E8 0 AMA Add Medium Aligned E8 01 AFA Add Floating Aligned E8 011 ADA Add Double Aligned E8 0111 AEA Add Extended Aligned EA 0 SMA Subtract Medium Aligned EA 01 SFA Subtract Floating Aligned EA 011 SDA Subtract Double Aligned EA 0111 SEA Subtract Extended Aligned EC 0 MMA Multiply Medium Aligned EC 01 MFA Multiply Floating Aligned EC 011 MDA Multiply Double Aligned EC 0111 MEA Multiply Extended Aligned EE 0 DMA Divide Medium Aligned EE 01 DFA Divide Floating Aligned EE 011 DDA Divide Double Aligned EE 0111 DEA Divide Extended Aligned
In order to double the space available to indicate registers in the Short Indexed instructions, there are no 48-bit indexed memory reference instructions for the byte data type, which would use up fully half of the opcode space available as they require an undiminished displacement field.
Only a tiny bit of space is left to include 32-bit versions of the conditional jump instructions and subroutine call instructions, but it can be made to serve.
The destination register field, while it serves to indicate where to store the return address for the jump to subroutine instruction, is unused for a jump instruction, and is therefore available to indicate the condition applicable to a conditional jump, as was done on the IBM System/360. This is complicated somewhat for the Short Indexed format, in which the destination register field has been reduced to three bits in length, but sufficient opcode space is still available.
Given that instructions are aligned on halfword boundaries, and there is no alternate kind of instruction that is aligned on 32-bit boundaries to jump to, both possible values of the one spare bit in the displacement may be used given that 16-bit alignment is the terminal alignment for this instruction type. This is needed because while there is extra space among the Aligned format instructions, none is available among the Short Indexed format instructions.
In order to fit the Short Indexed jump instructions in the limited space available, their format is modified. Only index registers 0 to 3 are available for them, unlike registers 0 to 7, made available for the other Short Indexed memory reference instructions. Also, since the destination register field is three bits long, instead of four, two opcodes rather than one are allocated to the conditional jump instructions.
E8 0 JSRA Jump to Subroutine Register Aligned E9 0 JSBA Jump to Subroutine Base Aligned EA1 0 JLA Jump if Low Aligned EA2 0 JEA Jump if Equal Aligned EA3 0 JLEA Jump if Low or Equal Aligned EA4 0 JHA Jump if High Aligned EA5 0 JNEA Jump if Not Equal Aligned EA6 0 JHEA Jump if High or Equal Aligned EA7 0 JNVA Jump if No Overflow Aligned EA8 0 JVA Jump if Overflow Aligned EAA 0 JCA Jump if Carry Aligned EAB 0 JNCA Jump if No Carry Aligned EAF 0 JA Jump Aligned E8 1 JSRX Jump to Subroutine Register Indexed E9 1 JSBX Jump to Subroutine Base Indexed EB0 1 JLX Jump if Low Indexed EA2 1 JEX Jump if Equal Indexed EB2 1 JLEX Jump if Low or Equal Indexed EA4 1 JHAX Jump if High Indexed EB4 1 JNEX Jump if Not Equal Indexed EA6 1 JHEX Jump if High or Equal Indexed EB6 1 JNVX Jump if No Overflow Indexed EA8 1 JVX Jump if Overflow Indexed EAA 1 JCX Jump if Carry Indexed EBA 1 JNCX Jump if No Carry Indexed EBE 1 JX Jump Indexed
Two versions of the Jump to Subroutine instruction are required; one saves the return address to a specified general register, the other to a specified base register. In the case of the Jump to Subroutine Base instruction, the possible targets are base registers 8 through 15, even though the instruction can only use base registers 11 through 15 with its destination address.
The Aligned instruction format clearly poses no issues, as it handles all non-indexed memory references well, with full four-bit fields available for both the destination register and the base register.
The Indexed instruction is hoped to be able to handle most indexed memory references, as the destination register can be anything from 0 to 3, and the index register anything from 1 to 7, and the base register field is used to indicate a base register from 8 to 15.
Adequate opcode space is still available for the 48-bit full memory reference instructions, multiple register instructions, and vector register instructions, despite their having been allocated only a very small portion of total opcode space.
Thus, for the full memory-reference instructions, we have:
FE 0nn
as the opcode, where nn is the opcode of the corresponding register-to-register instruction; i.e., we have
FE 024 A Add
for the instruction that performs 32-bit addition.
Also, there are the jump instructions:
FE 060 JSR Jump to Subroutine Register FE 061 JSB Jump to Subroutine Base FE1 062 JL Jump if Low FE2 062 JE Jump if Equal FE3 062 JLE Jump if Low or Equal FE4 062 JHA Jump if High FE5 062 JNE Jump if Not Equal FE6 062 JHE Jump if High or Equal FE7 062 JNV Jump if No Overflow FE8 062 JV Jump if Overflow FEA 062 JC Jump if Carry FEB 062 JNC Jump if No Carry FEF 062 J Jump FE 064 JXLE Jump if Index Low or Equal FE 065 JXH Jump if Index High
The Jump if Index Low or Equal instruction increments the general register indicated in the index register field, and jumps if its contents are less than or equal to those of the general register indicated in the destination register field. Jump if High decrements, and jumps if greater, instead.
This provides space for further expansion to handle additional data types.
To permit register-to-register instructions for additional data types, the opcode CF, which would indicate a Divide Extensibly Byte instruction if one were useful, can be used to indicate a 32-bit instruction that contains a 16-bit instruction in its second half and which provides additional opcode bits.
Thus, we have:
CF02 nnds FEdx 2nnb aaaa 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 SFSWH SFSW SFSWL 1 SFCH SFC SFCL 2 SFLH SFL SFLL 3 SFSTH SFST SFSTL 4 SFAH SFA SFAL 5 SFSH SFS SFSL 6 SFMH SFM SFML 7 SFDH SFD SFDL 8 SFMEUH SFMEU SFMEUL 9 SFDEUH SFDEU SFDEUL A SFLUH SFLU SFLUL B SFSTUH SFSTU SFSTUL C SFAUH SFAU SFAUL D SFSUH SFSU SFSUL E SFMUH SFMU SFMUL F SFDUH SFDU SFDUL
for the Simple Floating instructions,
CF03 nnds FEdx 3nnb aaaa 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 1 RPC RCDC 2 RPME RCDME 3 RPDE RCDDE 4 RPA RCDA 5 RPS RCDS 6 RPM RCDM 7 RPD RCDD 8 9 RPCL RCDCL A RPMEL RCDMEL B RPDEL RCDDEL C RPAL RCDAL D RPSL RCDSL E RPML RCDML F RPDL RCDDL
for the Register Packed Decimal and the Register Compressed Decimal instructions, and
CF04 nnds FEdx 4nnb aaaa 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 SWFRC SWDRC SWERC SWNFRC SWNDRC SWNERC 1 CFRC CDRC CERC CNFRC CNDRC CNERC 2 LFRC LDRC LERC LNFRC LNDRC LNERC 3 STFRC STDRC STERC STNFRC STNDRC STNERC 4 AFRC AFRCH ADRC AFDCH AERC AFDCH ANFRC ANDRC ANERC 5 SFRC SFRCH SDRC SFDCH SERC SFDCH SNFRC SNDRC SNERC 6 MFRC MFRCH MDRC MFDCH MERC MFDCH MNFRC MNDRC MNERC 7 DFRC DFRCH DDRC DFDCH DERC DFDCH DNFRC DNDRC DNERC 8 9 A LUFRC LUDRC LUERC B STUFRC STUDRC STUERC C AUFRC AUDRC AUERC D SUFRC SUDRC SUERC E MUFRC MUDRC MUERC F DUFRC DUDRC DUERC
for the Floating Register Compressed Decimal instructions.
Finally, rather than switching into a special mode for the Subdivided Floating and Subdivided Medium data types, they as well may be given their own instructions, although this will mean that the instructions are longer:
CF05 nnds FEdx 5nnb aaaa 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 SWSM 1 CSM 2 LSM 3 STSM STRSM STRM STRD 4 ASM 5 SSM 6 MSM 7 DSM 8 SWSF 9 CSF A LSF B STSF STRSF STRF C ASF D SSF E MSF F DSF
Store Rounded instructions are shown for both these formats and the regular floating-point formats other than Extended: they will be discussed below.
Thus, the floating-point formats available on this machine are the following:
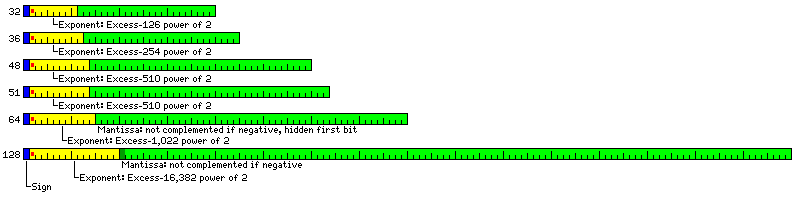
where Floating is 32 bits long, Subdivided Floating is 36 bits long, Medium is 48 bits long, Subdivided Medium is 51 bits long, Double is 64 bits long, and Extended is 128 bits long.
The formats are based on those specified by the IEEE 754 standard for 32 and 64 bit floating-point numbers. The sizes of the exponent fields for other sizes of floating-point numbers were chosen on the basis of the following rationales:
In the case of 36-bit floats, since the hidden first bit grants an extra bit of precision, the floating-point precision of the IBM 7090 can be attained while adding a bit to the exponent to approximate the exponent range of the IBM 360. This allows a broader range of older FORTRAN programs to run without modification if this type of number is used for single precision (provided, of course, that the unusual storage layout is not an issue).
In the case of 48-bit and 51-bit floats, the size of the exponent was chosen because these formats provide a precision of 11 or 12 decimal digits, thus approximating that provided by a typical scientific pocket calculator; therefore, it was deemed desirable that the exponent range exceed that of such a calculator as well (10^-99 to 10^99).
Medium floating point numbers, as can be seen from the instruction formats, are aligned on 16 bit boundaries. Floating, Double, and Extended numbers are aligned when placed on multiples of their lengths, as they have power-of-two lengths.
It is assumed that memory is connected to a microprocessor using this ISA by a 256-bit data bus. A 256 bit memory word can be divided into seven 36-bit Subdivided Floating numbers with three bits left over, and into five 51-bit Subdivided Medium floating numbers with one bit left over.
In order to avoid the slow operation of dividing by either five or seven when addressing numbers of these types, however, they are stored with some additional wastage.
32 Subdivided Floating numbers are stored in five 256-bit memory words, leaving the 33rd, 34th, and 35th slots vacant.
64 Subdivided Medium numbers are stored in thirteen 256-bit memory words, leaving the 65th slot vacant.
In this way, only multiplication plus a small table lookup is required to locate the Nth element of an array of numbers of these types for any value of N. Numbers of these types are addressed as if they are 32 bits long, with only the first seven or the first five positions in a 256-bit memory word being valid. When an instruction is indexed, the index is treated as a displacement in floating point numbers rather than one in bytes. The last five bits, in the case of Subdvided Floating, or the last six bits, in the case of Subdivided Medium, are used to indicate the position within a block, and the higher portion of the index is multiplied by the length of a block in 256-bit memory words.
The portion of the basic address, formed by the sum of the base register contents and the displacement field in the instruction, that indicates a 32-bit word within a 256-bit memory cell, when shifted as required to make it in units of 32 bits, is added to the index register contents before processing. In the indexed case, values of 7 or 5 or higher respectively will work properly, whereas only values of 0 to 6 or 0 to 4 are valid for Subdivided Floating and Subdivided Medium respectively without indexing.
Because Medium floating-point numbers do not work well with indexing if the inefficiency of occasional double memory accesses is not to be tolerated, while Subdivided Medium floating-point numbers do not have this issue, but do not allow overlapping offset arrays, it might be useful to mix both types in the same program.
Thus, some points about type interoperability need to be noted.
Internally, all conventional floating-point numbers will be stored with exponents as in the Extended floating point format, followed by a mantissa with the appropriate number of bits, which will be one more than for the external form of any size other than Extended, as there will be no hidden first bit. (Note that these notes apply only to this architecture, not the parent architecture to which reference is made for the definitions of some exotic data types; that architecture allows considerably more flexibility in floating-point formats, and so it needs to do type conversions explicitly and store all numbers internally in their memory format.)
The floating-point registers, however, are still essentially 128-bit wide fast memory locations without special circuitry; the internal format simply allows numbers to be quickly fed to the floating-point ALU. This permits flexibility in register renaming. (This particular item is a characteristic of the parent architecture as well.)
Floating-point operations clear all the unused less significant mantissa bits. But storing a floating-point number at a lesser precision involves truncation, not rounding, to avoid imposing an overhead on the great majority of operations which involve numbers being stored at their own precision. This conflicts with the aim of the IEEE 754 standard to retain the maximum possible accuracy in all calculations, and, thus, the Store Rounded instructions, placed in the same region of opcode space as the Subdivided floating-point instructions are provided.
The Floating Register Compressed Decimal numbers are also stored in the floating-point registers. Because they are actually 128 bits long, the internal and external formats of 128-bit Floating Register Compressed Decimal numbers are the same. For maximum efficiency in handling decimal floating-point numbers of other precisions, they are stored internally as a sign, a 15-bit binary exponent, and seven or sixteen BCD digits. So Chen-Ho (or, rather, Densely Packed Decimal) encoding and decoding is combined with memory operations for the shorter formats, but is done during register operations for the extended precision.
The short vector instructions also require an additional field to indicate the mask register being used, and another to indicate if masking is present, so they're 16 bits longer. Fortunately, even among 48-bit instructions, there is space for extra codes, using F8 as the opcode:
FE00 1nn0 mMds F801 nn0d mMxb aaaa
0 1 2 3 4 5 6
0 SWBSV SWHSV SWSV SWLSV SWFSV SWDSV SWESV
1
2 LBSV LHSV LSV LLSV LFSV LDSV LESV
3 STBSV STHSV STSV STLSV STFSV STDSV STESV
4 ABSV AHSV ASV ALSV AFSV ADSV AESV
5 SBSV SHSV SSV SLSV SFSV SDSV SESV
6 MHSV MSV MLSV MFSV MDSV MESV
7 DHSV DSV DLSV DFSV DDSV DESV
8 SMBPB SMBPH SMBP SMBPL SMBPF SMBPD SMBPE
9 SMBZB SMBZH SMBZ SMBZL SMBZF SMBZD SMBZE
A SMBNB SMBNH SMBN SMBNL SMBNF SMBND SMBNE
B XBSV XHSV XSV XLSV
C NBSV NHSV NSV NLSV
D OBSV OHSV OSV OLSV
E
F
Key to the instruction formats:
nn: opcode as indicated in the table
aaaa: address displacement field
m: 0000 if no mask, 0001 if masked
M: mask register
d: destination register
s: source register
x: index register
b: base register
and, of course, mnemonics are suffixed R for register to register instructions.
In the case of the multiple register and the vector register instructions, the secondary opcode field is eight bits long rather than twelve, but this is still sufficient:
FE 0 82 LBVR Load Byte Vector Register
(and so forth)
FE 4 82 LMVR Load Medium Vector Register
(and so forth)
FE 4 D0 SWSMVR Swap Subdivided Medium Vector
(and so forth)
FE F2 LM Load Multiple
FE F3 STM Store Multiple
FE F4 LML Load Multiple Long
FE F5 STML Store Multiple Long
FE F6 LME Load Multiple Extended
FE F7 STME Store Multiple Extended
Because the first digit of the seconary opcode field of these instructions is 8 or greater, to distinguish them from the full memory reference instructions, the primary opcode field contains the first digit of the two-digit opcode of the analogous instruction, with the first digit of the secondary opcode field containing 8 plus the supplementary opcode digit, and the second digit of the secondary opcode field containing the second digit of the analogous instruction.
Thus, a full memory reference instruction with opcode 123, analogous to a register to register instruction with opcode 23, would correspond to a vector instruction with the split opcode 2 93.
The vector memory-reference instructions are 80 bits long, rather than 64 bits long, partly because of a serious shortage of opcode space for the 64-bit long packed decimal and string instructions, on the other hand.
For the 80-bit instructions, we have:
FF 0 02 LBV Load Byte Vector
(and so forth)
FF 4 02 LMV Load Medium Vector
(and so forth)
FF 4 50 SWSMV Swap Subdivided Medium Vector
(and so forth)
FF A TR Translate
FF C FMT Format
FF E SC Scan
Because the first bit of the secondary opcode must be zero, to distinguish it from the translate instructions, once again the prefix digit becomes the first digit of the secondary opcode, and the two digits of the corresponding original opcode become the primary opcode and the second digit of the secondary opcode respectively. Thus, the opcode 123 becomes 2 13.
While indexing works properly with Subdivided Medium and Subdivided Floating vector operations, remember that the address pointed to by the base and the displacement always defines the beginning of a block of floats with unused space at the end (even though it does not have to point to the very first element of that block), and so it is not possible, in general, to have overlapping vectors work the way one would expect from datatypes which fit more neatly into storage.
The rule to remember is that the counter locating array elements for a vector operation is treated like an index register for purposes of address formation with Subdivided floating-point numbers; even stride works properly with them without issues.
Also, not only are vector operations on 51-bit Subdivided Medium numbers are allowed, vector operations on 48-bit Medium numbers are also supported: while elements of such vectors would cross memory word boundaries, since handling a vector from memory involves fetching each memory word once, not repeatedly for each element containing it, no actual efficiency issue results during vector operations, provided no nonunit stride is present, although one would exist when operating on those individual elements that cross such boundaries.
The FMT instruction operates as follows: The first operand is a translation table with 256 one-byte entries in which entries 0, 1, and 255 have a special significance. The length field of the instruction determines the length of the source operand. Successive characters from the source operand are moved to the destination operand as follows:
This instruction, except that it does not convert from packed decimal to unpacked, performs a similar function to the edit and edit with mark instructions on the IBM System/360 computer. Thus, a translation table can contain a fill character in position 0, the digit zero in position 1, and a floating currency symbol (or another fill character) in position 255 to convert a raw zoned decimal string (produced by an unpack instruction) to the format used in printing. Note that the decimal point would be placed in the destination operand, with zero bytes in the positions to be filled with digits.
The SC instruction begins by ignoring any characters in the source operand that translate to bytes containing zero in the translation table; then, bytes not translating to zero are copied with translation until an entry in the translate table containing a zero is encountered. The number of characters translated is placed in accumulator/index register 2, giving the length of the result in the destination operand, and the number of characters translating to zero that were initially ignored, plus the number of characters translated, is placed in accumulator/index register 1, giving the portion of the source operand that was scanned until the first character translating to zero following a character not translating to zero was found, and the remainder of the destination operand is filled with the character found in position 0 of the translate table.
The source operand may not contain a byte having the value 0. If it does, the instruction stops, and an overflow condition is set.
If the instruction completes within the provided length, then it is treated as having a zero result for a subsequent conditional branch instruction; if it did not complete, but characters with nonzero translations were encountered, it has a positive result; if only characters translating to zero were encountered, it has a negative result.
This instruction can be used for some of the same purposes as the translate and test instruction of the IBM System/360, although it works differently. It can be used to scan for keywords and translate them to upper case, for example.
and as for the 64-bit instructions, they do still squeeze in:
F1 CP Compare Packed F2 MVP Move Packed F4 AP Add Packed F5 SP Subtract Packed F6 MP Multiply Packed F7 DP Divide Packed FA MVB Move Byte FC P Pack FD UP Unpack
Note that the Pack and Unpack instructions take a packed argument that is half the length of the argument that would be indicated if it were in character form: these instructions have a single length field, like the MVB instruction. Unpack adds hexadecimal 30 to each packed decimal digit, converting it to an ASCII digit.
The length fields of these instructions contain one minus the operand length.